Lavaldüse

Lavaldüse im Schnitt mit Flussrichtung des Mediums

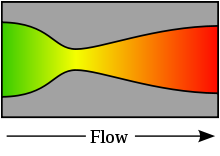
Die Lavaldüse ist eine von Ernst Körting 1878 für Dampfstrahlapparate und dem Schweden Carl Gustav Patrik de Laval 1883 für die Beaufschlagung von Dampfturbinen mit Wasserdampf unabhängig voneinander entwickelte Düse. Der Querschnitt der Lavaldüse verengt sich zunächst und weitet sich bis zum Gasaustritt wieder auf, wodurch ein durchströmendes Fluid auf Überschallgeschwindigkeit beschleunigt werden kann, ohne dass es zu starken Verdichtungsstößen kommt. Die Schallgeschwindigkeit wird genau im engsten Querschnitt der Düse erreicht.

Lavaldüsen werden bereits seit der V2 und auch heute bei Raketentriebwerken verwendet.

Herleitung

Die Schallgeschwindigkeit a ist eine von der Dichte ρ des Mediums abhängige Größe. Das Verhältnis der Strömungsgeschwindigkeit c eines Mediums zu seiner Schallgeschwindigkeit a wird auch als Mach-Zahl M bezeichnet:

(1) $M = \frac{c}{a}$

Die Eulersche Bewegungsgleichung ergibt zusammen mit der Zustandsgleichung dp / dρ = a²:

$c \frac{dc}{dx} = - \frac{1}{\rho} \frac{dp}{dx} = - \frac{1}{\rho} \frac{dp}{d\rho} \frac{d\rho}{dx} = - \frac{a^2}{\rho} \frac{d\rho}{dx}$,

(2) $\frac{1}{\rho} \frac{d\rho}{dx} = -M^2 \frac{1}{c} \frac{dc}{dx}$,

wobei ρ die Dichte des Mediums, x die Strömungsrichtung ist.

Gleichung (2) sagt aus, dass die relative Dichteänderung der relativen Geschwindigkeitsänderung längs des Stromfadens proportional ist, wobei der Proportionalitätsfaktor M ² ist. Aus dem quadratischen Proportionalitätsfaktor folgt, dass bei einer Unterschallströmung (M<1) die relative Dichteänderung (wesentlich) kleiner als die relative Geschwindigkeitsänderung ist, umgekehrt bei einer Überschallströmung (M>1) die relative Dichteänderung (wesentlich) größer als die relative Geschwindigkeitsänderung ist.

Ferner muss noch die Kontinuitätsgleichung betrachtet werden:

$\rho c A = \mathsf{const}$,

$\ln \rho + \ln c + \ln A = \ln(\mathsf{const})$,

$\frac{d\rho}{\rho} + \frac{dc}{c} + \frac{dA}{A} = 0$.

Differenziert man dies längs des Stromfadens, so ergibt sich

$\frac{1}{\rho} \frac{d\rho}{dx} + \frac{1}{c} \frac{dc}{dx} + \frac{1}{A} \frac{dA}{dx} = 0$.

Unter Berücksichtigung von (2) folgt daraus

(3) $\frac{1}{c} \frac{dc}{dx} = \frac{1}{M^2 - 1} \frac{1}{A} \frac{dA}{dx}$.

Nimmt man die Querschnittsfläche A(x) als gegeben, c(x) und M(x) als unbekannt an, ermöglicht (3) eine qualitative Diskussion der Strömung einer Düse. Will man eine Strömung beschleunigen, also dc/dx > 0, so folgt aus (3)

• für Unterschallströmung (M < 1), dass dA/dx < 0 sein muss, sich die Düse also verengen muss,
• für Überschallströmung (M > 1), dass dA/dx > 0 sein muss, sich die Düse also erweitern muss und
• für Schallströmung (M = 1) die Düse einen konstanten Querschnitt haben muss.

Lavaldüse

Daraus folgt ganz zwangsläufig die Form der Lavaldüse. Im konvergenten Teil wird die Unterschallströmung beschleunigt. Am engsten Querschnitt erreicht sie Schallgeschwindigkeit. Im divergenten Teil schließlich wird die Strömung weiter beschleunigt, erreicht also Überschallgeschwindigkeit.

Siehe auch

• Düse
• Venturi-Düse