Least Mean Squares

Der LMS-Algorithmus (Least-Mean-Squares-Algorithmus) ist ein Algorithmus zur Approximation der Lösung des Least-Mean-Squares Problems, das z. B. in der digitalen Signalverarbeitung vorkommt. In der Neuroinformatik ist der Algorithmus vor allem als Delta-Regel oder Widrow-Hoff-Regel bekannt.

Der Algorithmus beruht auf der sogenannten Methode des steilsten Abstiegs (Gradientenverfahren) und schätzt den Gradienten auf einfache Art. Der Algorithmus arbeitet zeitrekursiv, d. h. mit jedem neuen Datensatz wird der Algorithmus einmal durchlaufen und die Lösung aktualisiert. Die Regel wurde erstmals 1960 von Bernard Widrow und Marcian Edward Hoff für das Einlernen des Adaline-Modells verwendet.

Der LMS-Algorithmus wird auf Grund seiner geringen Komplexität häufig eingesetzt. Einsatzgebiete sind u. a. adaptive Filter, adaptive Regelungen und Online-Identifikationsverfahren.

Ein bedeutender Nachteil des LMS-Algorithmus ist die Abhängigkeit seiner Konvergenzgeschwindigkeit von den Eingangsdaten, d. h. der Algorithmus findet unter ungünstigen Umständen möglicherweise keine Lösung. Ungünstige Umstände sind die schnelle zeitliche Änderung der Eingangsdaten.

Algorithmus

Ziel sei es die Koeffizienten eines FIR-Filters so zu bestimmen, dass der Fehler zwischen Ausgangsdaten der Filters 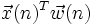$\vec x(n)^T \vec w(n)$ und vorgegebenen Referenzdaten y(n) minimiert wird.

Der LMS-Algorithmus hat dann folgende Form:

$e(n) = y(n) - \vec x(n)^T \vec w(n)$

$\vec w(n+1) = \vec w(n) + \mu e(n) \vec x(n)$

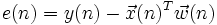
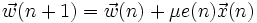
Dabei ist 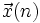$\vec x(n)$ ein Vektor mit Eingangsdaten der Zeitpunkte n-(M+1) bis n, y(n) ein Referenzdatum zum Zeitpunkt n, 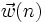$\vec w(n)$ der aktuelle Vektor der Filtergewichte des Transversalfilters der Ordnung M, μ ein Faktor zur Einstellung der Geschwindigkeit und Stabilität der Adaption und 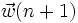$\vec w(n+1)$ der neu zu bestimmende Filtervektor der Ordnung M. Es wird also zu jedem Zeitpunkt der aktuelle Fehler bestimmt und daraus die neuen Filtergewichte 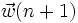$\vec w(n+1)$ berechnet.

Verwendung in der Neuroinformatik

Der LMS-Algorithmus gehört zur Gruppe der überwachten Lernverfahren. Dazu muss ein externer Lehrer existieren, der zu jedem Zeitpunkt der Eingabe die gewünschte Ausgabe, den Zielwert, kennt.

Er kann auf jedes einschichtige künstliche neuronale Netz angewendet werden, dabei muss die Aktivierungsfunktion differenzierbar sein. Das Backpropagation-Verfahren verallgemeinert diesen Algorithmus und kann auch auf mehrschichtige Netze angewandt werden.