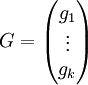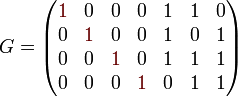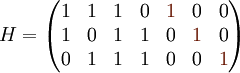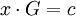Linearcode

Ein Linearer Code ist in der Kodierungstheorie ein spezieller Blockcode: Man betrachtet die Blöcke als endlichdimensionale Vektorräume über einem endlichen Körper 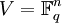$V=\mathbb{F}_q^n$. Ein Code ist genau dann ein Linearer Code C , falls er ein Untervektorraum von V ist.

Die Linearen Codes haben den Vorteil, dass Methoden der Linearen Algebra verwendet werden können. Sie sind somit einfach zu codieren und decodieren. Die meisten wichtigen Codes sind linear: Hamming-Code, Reed-Muller-Code, Hadamard-Code, alle zyklischen Codes (Damit auch BCH und Reed-Solomon Codes), Golay Codes, Goppa-Codes.

Ist die Vektorraumdimension von C gleich k, so nennt man C einen [n,k]-Code, oder bei einem Hammingabstand von d auch [n,k,d]-Code.

Eigenschaften

Da C ein Untervektorraum von V ist, existiert eine Basis 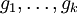$g_1, \dots, g_k$ von C. Fasst man diese Basis in einer Matrix

$G=\begin{pmatrix} g_1 \\ \vdots\\ g_k \end{pmatrix}$

zusammen, erhält man eine Erzeugermatrix. Des Weiteren besitzt der Code eine Kontrollmatrix H. Für sie gilt Hc^T = 0 genau dann, wenn c ein Codewort ist. Der Rang von G ist k, der von H ist n − k. Der Hammingabstand von C ist die minimale Anzahl linear abhängiger Spalten der Kontrollmatrix.

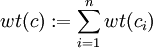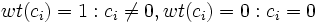Ist $wt(c):= \sum_{i=1}^n wt(c_i)$ mit $wt(c_i) = 1 : c_i \not= 0 , wt(c_i) = 0 : c_i = 0$ das Hamminggewicht eines Codewortes 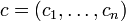$c=(c_1,\dots,c_n)$, dann ist der Hammingabstand gleich dem minimalem Hamminggewicht aller Codewörter außer dem Nullwort.

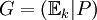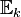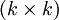Permutiert man die einzelnen Koordinaten der Codewörter, dann erhält man einen sogenannten äquivalenten Code. Damit und mittels linearer Algebra kann man zu jedem linearen Code einen äquivalenten finden, der eine Erzeugermatrix der Form $G=(\mathbb{E}_k|P)$ hat. Dabei ist $\mathbb{E}_k$ die $(k \times k)$-Einheitsmatrix, und P ist eine 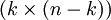$(k \times (n-k))$-Matrix. Dann heißt G Erzeugermatrix in reduzierter Form. Die ersten k Koordinaten können als Informationssymbole und die letzten n − k als Kontrollsymbole interpretiert werden. Ist G eine Erzeugermatrix in reduzierter Form, kann eine Kontrollmatrix H sofort gefunden werden: 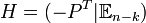$H=(-P^T|\mathbb{E}_{n-k})$. Ein linearer Code ist bereits durch seine Erzeugermatrix oder seine Kontrollmatrix bestimmt.

Beispiel

Der [7,4,3]-Hammingcode besitzt folgende Erzeugermatrix in reduzierter Form, sowie die dazugehörige Kontrollmatrix.

$G=(\mathbb{E}_k|P)$		$H=(-P^T|\mathbb{E}_{n-k})$
$G= \begin{pmatrix} {\color{Brown}1} & 0 & 0 & 0 & 1 & 1 & 0 \\ 0 & {\color{Brown}1} & 0 & 0 & 1 & 0 & 1 \\ 0 & 0 & \color{Brown}{1} & 0 & 1 & 1 & 1 \\ 0 & 0 & 0 & {\color{Brown}1} & 0 & 1 & 1 \\ \end{pmatrix} \qquad$		$H= \begin{pmatrix} 1 & 1 & 1 & 0 & {\color{Brown}1} & 0 & 0 \\ 1 & 0 & 1 & 1 & 0 & {\color{Brown}1} & 0 \\ 0 & 1 & 1 & 1 & 0 & 0 & {\color{Brown}1} \\ \end{pmatrix}$

Codierung

Ein Wort 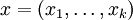$x=(x_1, \dots, x_k)$ aus dem Raum 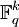$\mathbb{F}_q^k$ wird codiert, indem das Produkt xG gebildet wird. Soll beispielsweise das Wort (0,0,1,1) mit dem [7,4,3,2]-Hammingcode codiert werden, sieht das so aus:

$x \cdot G = c$

$\begin{pmatrix}0,0,1,1\end{pmatrix} \cdot \begin{pmatrix} 1 & 0 & 0 & 0 & 1 & 1 & 0 \\ 0 & 1 & 0 & 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 0 & 1 & 1 & 1 \\ 0 & 0 & 0 & 1 & 0 & 1 & 1 \\ \end{pmatrix} =\begin{pmatrix}0,0,1,1,1,0,0\end{pmatrix}$.

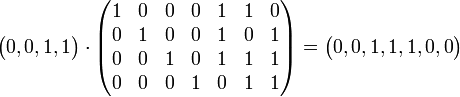Man beachte, dass hier die Multiplikation in 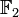$\mathbb{F}_2$ erfolgt, also modulo 2.

Decodierung (Syndromdecodierung)

Als Decodierung wird in der Codierungstheorie die maximum-likelihood Methode verwendet, sprich ein empfangenes Wort x wird zu dem Codewort c decodiert, welches den geringsten Hammingabstand zu x hat. Es sei e = x − c, e wird Fehlervektor genannt. In e sind genau die Koordinaten ungleich Null, bei denen während der Übertragung Fehler auftraten. Nun sind alle (fehlerhaften) Wörter mit dem gleichen Fehlervektor im gleichen affinen Unterraum. Deshalb ist für solche Worte z^T = He^T konstant.

Daraus resultiert folgende Decodierregel: Wähle für jeden möglichen Fehlervektor e jeweils das Wort mit minimalem Hamminggewicht, also das mit möglichst wenigen Koordinaten ungleich Null; und damit sozusagen ein "fehlerhaftes" Nullwort. Für jedes dieser Worte berechne man z^T = He^T und speichere diese Paare. Man kann somit für jedes z den dazugehörenden Fehlervektor e = e(z) berechnen. Um dann ein empfanges Wort x zu decodieren berechnet man dann c(x): = x − e(Hx^T). Damit erhält man ein gültiges Codewort, ist G noch in reduzierter Form, kann dann die Information einfach an den ersten k Symbolen abgelesen werden (falls nicht muss eventuell noch ein lineares Gleichungssystem gelöst werden). e heißt dabei Nebenklassenführer (engl. Cosetleader) und z Syndrom.

Formal erklärt sich die Regel wie folgt: Sei x das zu decodierende Wort, aber x liege nicht in C. Sei c der Vektor in C der einen minimalen Hammingabstand zu x hat. Definieren dann den Fehlervektor e=x-c. Somit suchen wir ein Element e mit minimalem Gewicht aus der Nebenklasse (engl. Coset) x − C. Sei H die Kontrollmatrix zu C. Dann gilt $x_1-x_2 \in C$ genau dann wenn $H\cdot x_1^T=H\cdot x_2^T$ gilt. Wenn wir ein x gegeben haben suchen wir den Fehler e mit $x-e \in C$ der minimales Gewicht hat.

Beispiel

Will man den [7,4,3]-Hammingcode (von oben) decodieren, trifft man zuerst die Annahme, dass nur 1-Bit Fehler auftreten (falls mehr Fehler auftreten ist keine Fehlerkorrektur sondern nur noch eine Fehlererkennung möglich). Die möglichen Fehlervektoren e sind dann

(1,0,0,0,0,0,0)

(0,1,0,0,0,0,0)

(0,0,1,0,0,0,0)

(0,0,0,1,0,0,0)

(0,0,0,0,1,0,0)

(0,0,0,0,0,1,0)

(0,0,0,0,0,0,1)

Für jeden dieser Fehlervektoren wird nun das Syndrom z^T = He^T berechnet. Damit ergibt sich

e	z
(0,0,0,0,0,0,0)	(0,0,0)
(1,0,0,0,0,0,0)	(1,1,0)
(0,1,0,0,0,0,0)	(1,0,1)
(0,0,1,0,0,0,0)	(1,1,1)
(0,0,0,1,0,0,0)	(0,1,1)
(0,0,0,0,1,0,0)	(1,0,0)
(0,0,0,0,0,1,0)	(0,1,0)
(0,0,0,0,0,0,1)	(0,0,1)

Wird dann das fehlerhafte Wort x = (0,1,1,1,1,0,0) empfangen ergibt dann z^T = Hx^T = (1,0,1)^T. Damit ergibt sich der Fehlervektor e = e((1,0,1)) = (0,1,0,0,0,0,0) und x wird somit nach c(x) = (0,1,1,1,1,0,0) − (0,1,0,0,0,0,0) = (0,0,1,1,1,0,0) decodiert und das Klartextwort ist dann (0,0,1,1).

Anwendung

Die Codierung und Decodierung ist, so wie sie oben beschrieben ist, relativ aufwendig. Bei der Codierung muss die Erzeugermatrix im Speicher gehalten werden, was bei Systemen mit begrenzten Ressourcen (zum Beispiel mobile Endgeräte oder Weltraumsonden) problematisch ist. Bei der Decodierung wird eine - je nach Korrekturrate - große Tabelle benötigt, der Speicherverbrauch ist dementsprechend groß. Aus diesem Grund werden in der Regel zusätzliche Eigenschaften der Codes benutzt um diese effizient zu codieren und decodieren. Binäre Zyklische Codes lassen sich beispielsweise sehr einfach mittels Schieberegister und XOR Gatter realisieren.

Literatur

• Werner Lütkebohmert: Codierungstheorie. Vieweg Verlag, 2003, ISBN 3-528-03197-2
• J. H. van Lint: Introduction to Coding Theory. Springer Verlag, 1999, ISBN 3-540-64133-5
• F. J. MacWilliams, N. J. A. Sloane: The Theory of Error-Correcting Codes. North-Holland publishing company, 1978