- Lineare Rekursion
-
Lineare Differenzengleichungen oder lineare Rekursionsgleichungen sind Beziehungen einer besonders einfachen Form zwischen den Gliedern einer Folge. Das bekannteste Beispiel ist die Fibonacci-Folge
für natürliche Zahlen n, konkret
- 0, 1, 1, 2, 3, 5, 8, 13, …
Jedes Folgenglied (abgesehen von den Anfangswerten) ist also die Summe der beiden vorherigen.
Allgemein nennt man jede Gleichung der Form
- an + 1 = uan + van − 1
mit v von Null verschieden eine (homogene) lineare Differenzengleichung 2. Ordnung (mit konstanten Koeffizienten).
Inhaltsverzeichnis
Lösungstheorie homogener linearer Differenzengleichungen 2. Ordnung
Die erste Idee zur Lösung besteht in der Beobachtung, dass derartige Folgen meist exponentiell wachsen. Das legt den ersten Ansatz an = λn mit einem von Null verschiedenen Lambda nahe. Eingesetzt ergibt das
- λn + 1 = uλn + vλn − 1,
nach Division durch λn − 1 also
- λ2 − uλ − v = 0.
Diese quadratische Gleichung heißt charakteristische Gleichung der Rekursion. Folgen der Form an = λn mit einem λ, das (reelle oder komplexe) Lösung der charakteristischen Gleichung ist, erfüllen also die gewünschte Rekursionsgleichung.
Die zweite Idee ist die der Linearkombination: Sind an und bn Folgen, die die Rekursionsgleichung erfüllen, so gilt das auch für
- cn = xan + ybn
für beliebige (reelle oder komplexe) Zahlen x,y. (Man kann das auch so ausdrücken: Die Menge aller Folgen, die die Rekursionsgleichung erfüllen, bildet einen Vektorraum.)
Sind jetzt Anfangswerte a0,a1 gegeben, und hat die charakteristische Gleichung zwei verschiedene Lösungen λ1,λ2, so können die Koeffizienten x,y aus dem folgenden linearen Gleichungssystem bestimmt werden:
Dann gilt
 für alle n.
für alle n.Im Beispiel der Fibonacci-Folge sind
es ergibt sich also die so genannte Binet-Formel
Sonderfall: Die charakteristische Gleichung hat eine doppelte Lösung
Hat die charakteristische Gleichung nur eine Lösung, d. h. eine doppelte Lösung Lambda, so hat die allgemeine Lösung die Form
- an = xλn + ynλn.
Beispielsweise erfüllt an = n (also x = 0,y = 1,λ = 1) die Rekursionsgleichung
- an + 1 = 2an − an − 1.
Allgemeine Theorie
Eine Lineare Differenzengleichung k-ter Ordnung über einem Körper
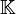 ist von der Form:
ist von der Form:
,mit  und
und 
Ist die rechte Seite b(n) = 0 für alle
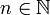 , dann heißt die Gleichung homogen. Ansonsten heißt sie inhomogen. Eine homogene Gleichung hat stets die triviale Lösung f(n) = 0.
, dann heißt die Gleichung homogen. Ansonsten heißt sie inhomogen. Eine homogene Gleichung hat stets die triviale Lösung f(n) = 0.Rechenregeln
Satz 1
Sind f1 und f2 Lösungen der homogenen linearen Differenzgleichung
 , dann ist auch αf1 + βf2 für beliebige
, dann ist auch αf1 + βf2 für beliebige 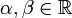 eine Lösung.
eine Lösung.Satz 2
Sind f1 und f2 Lösungen der inhomogenen linearen Differenzengleichung
 , dann ist f1 - f2 eine Lösung der zugehörigen homogenen linearen Differenzgenleichung mit b(n) = 0 für alle
, dann ist f1 - f2 eine Lösung der zugehörigen homogenen linearen Differenzgenleichung mit b(n) = 0 für alle 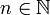 .
.Satz 3
Ist f1 eine Lösung der inhomogenen linearen Differenzengleichung
 und f2 eine Lösung der zugehörigen homogenen linearen Differenzengleichung mit b(n) = 0 für alle
und f2 eine Lösung der zugehörigen homogenen linearen Differenzengleichung mit b(n) = 0 für alle 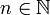 , dann ist auch f1 + αf2 für beliebige
, dann ist auch f1 + αf2 für beliebige 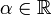 eine Lösung der inhomogenen linearen Differenzengleichung.
eine Lösung der inhomogenen linearen Differenzengleichung.Lösung linearer Differenzengleichungen mit konstanten Koeffizienten
Eine lineare Differenzengleichung mit konstanten Koeffizienten hat die Form
 . Alle ai sind konstant.
. Alle ai sind konstant.Lösung der homogenen Gleichung
Mit dem Ansatz f(n) = λn wird eine nichttriviale Lösung der homogenen Gleichung
 ermittelt.
ermittelt.Dies führt auf die charakteristische Gleichung
 .
.Die verschiedenen Nullstellen der Gleichung ergeben dann linear unabhängige Lösungsfolgen und damit Lösungen der homogenen Gleichung.
Sind die Nullstellen nicht verschieden, so kommt die zu einer mehrfachen Nullstelle gehörende Lösungsfolge mit einem Faktor in der Lösung vor, der ein Polynom in n mit einem Grad kleiner als die Vielfachheit der Nullstelle ist.
Beispiel:
-

homogene Differenzengleichung 
Ansatz: xn = λn 
charakteristische Gleichung mit 

Lösung der Gleichung als Linearkombination spezieller Lösungen, Konstanten können aus Anfangsbedingungen bestimmt werden.
Partikuläre Lösung
Die Bestimmung geschieht hier analog zu Differentialgleichungen.
Störfunktion b(n) Ansatz partikuläre Lösung Konstante Konstante Polynom Polynom gleichen Grades un 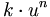

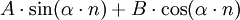
Falls der Ansatz bereits eine Lösung der zugehörigen homogenen Differenzengleichung sein sollte, ist er mit n,n2,n3 zu multiplizieren, bis er eine Lösung der inhomogenen Gleichung liefert.
Beispiel
Gegeben ist eine Folge an mit
 . Gesucht ist die explizite Formel. Wir suchen zuerst die allgemeine Lösung für die homogene Rekursionsgleichung.
. Gesucht ist die explizite Formel. Wir suchen zuerst die allgemeine Lösung für die homogene Rekursionsgleichung.-

inhomogene Rekursionsgleichung 
homogene Rekursionsgleichung, Ansatz: 

Kürzen von λn, Lösungen λ = 0 verfallen. 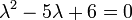
Charakteristische Gleichung, Lösungen: λ1 = 2 und λ2 = 3 
Allgemeine Lösung der homogenen Rekursionsgleichung
Nun suchen wir eine spezielle Lösung der inhomogenen Rekursionsgleichung, die partikuläre Lösung.
-

inhomogene Rekursionsgleichung, Ansatz: 
-

Lösung: 

Partikuläre Lösung
Gemäß Satz 3 erhalten wir mit
 alle Lösungen der inhomogenen Rekursionsgleichung. Nun müssen c1 und c2 nur noch so bestimmt werden, dass a0 = 2 und a1 = 5 gilt.
alle Lösungen der inhomogenen Rekursionsgleichung. Nun müssen c1 und c2 nur noch so bestimmt werden, dass a0 = 2 und a1 = 5 gilt.-


I (n = 0) 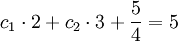
II (n = 1) 
III = II - 2 * I 
Durch Einsetzen in I erhalten wir außerdem 
Also ist
 die gesuchte Formel.
die gesuchte Formel.Siehe auch
Literatur
- Berg, L.: Lineare Gleichungssysteme mit Bandstruktur, München-Wien: Carl Hanser, 1986
- Ian Jaques. Mathematics for Economics and Business, Fifth Edition. Prentice Hall, 2006. ISBN 0-273-70195-9. Chapter 9.1: Difference Equations, pp.551–568.
Wikimedia Foundation.






