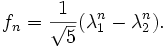Lineare Rekurrenz

Lineare Differenzengleichungen oder lineare Rekursionsgleichungen sind Beziehungen einer besonders einfachen Form zwischen den Gliedern einer Folge. Das bekannteste Beispiel ist die Fibonacci-Folge

$f_0 = 0,\quad f_1 = 1,\quad f_{n+1} = f_n + f_{n-1}$

für natürliche Zahlen n, konkret

0, 1, 1, 2, 3, 5, 8, 13, …

Jedes Folgenglied (abgesehen von den Anfangswerten) ist also die Summe der beiden vorherigen.

Allgemein nennt man jede Gleichung der Form

a_{n + 1} = ua_n + va_{n − 1}

mit v von Null verschieden eine (homogene) lineare Differenzengleichung 2. Ordnung (mit konstanten Koeffizienten).

Lösungstheorie homogener linearer Differenzengleichungen 2. Ordnung

Die erste Idee zur Lösung besteht in der Beobachtung, dass derartige Folgen meist exponentiell wachsen. Das legt den ersten Ansatz a_n = λⁿ mit einem von Null verschiedenen Lambda nahe. Eingesetzt ergibt das

λ^{n + 1} = uλⁿ + vλ^{n − 1},

nach Division durch λ^{n − 1} also

λ² − uλ − v = 0.

Diese quadratische Gleichung heißt charakteristische Gleichung der Rekursion. Folgen der Form a_n = λⁿ mit einem λ, das (reelle oder komplexe) Lösung der charakteristischen Gleichung ist, erfüllen also die gewünschte Rekursionsgleichung.

Die zweite Idee ist die der Linearkombination: Sind a_n und b_n Folgen, die die Rekursionsgleichung erfüllen, so gilt das auch für

c_n = xa_n + yb_n

für beliebige (reelle oder komplexe) Zahlen x,y. (Man kann das auch so ausdrücken: Die Menge aller Folgen, die die Rekursionsgleichung erfüllen, bildet einen Vektorraum.)

Sind jetzt Anfangswerte a₀,a₁ gegeben, und hat die charakteristische Gleichung zwei verschiedene Lösungen λ₁,λ₂, so können die Koeffizienten x,y aus dem folgenden linearen Gleichungssystem bestimmt werden:

$a_0 = x\lambda_1^0 + y\lambda_2^0 = x + y$

$a_1 = x\lambda_1^1 + y\lambda_2^1 = x\lambda_1 + y\lambda_2$

Dann gilt $a_n = x\lambda_1^n + y\lambda_2^n$ für alle n.

Im Beispiel der Fibonacci-Folge sind

$\lambda_{1/2}=\frac{1\pm\sqrt5}2,\quad x=\frac1{\sqrt5}=-y,$

es ergibt sich also die so genannte Binet-Formel

$f_n=\frac1{\sqrt5}(\lambda_1^n - \lambda_2^n).$

Sonderfall: Die charakteristische Gleichung hat eine doppelte Lösung

Hat die charakteristische Gleichung nur eine Lösung, d. h. eine doppelte Lösung Lambda, so hat die allgemeine Lösung die Form

a_n = xλⁿ + ynλⁿ.

Beispielsweise erfüllt a_n = n (also x = 0,y = 1,λ = 1) die Rekursionsgleichung

a_{n + 1} = 2a_n − a_{n − 1}.

Allgemeine Theorie

Eine Lineare Differenzengleichung k-ter Ordnung über einem Körper 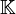$\mathbb K$ ist von der Form:

$\sum_{i=0}^k a_i(n)f(n+i) = b(n)$

,mit $a_i(n)\in \mathbb K$ und $a_k(n)\not=0$

Ist die rechte Seite b(n) = 0 für alle $n \in \mathbb{N}$, dann heißt die Gleichung homogen. Ansonsten heißt sie inhomogen. Eine homogene Gleichung hat stets die triviale Lösung f(n) = 0.

Rechenregeln

Satz 1

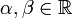Sind f₁ und f₂ Lösungen der homogenen linearen Differenzgleichung $\sum_{i=0}^k a_i(n)f(n+i) = b(n)$, dann ist auch αf₁ + βf₂ für beliebige $\alpha , \beta \in \mathbb{R}$ eine Lösung.

Satz 2

Sind f₁ und f₂ Lösungen der inhomogenen linearen Differenzengleichung $\sum_{i=0}^k a_i(n)f(n+i) = b(n)$, dann ist f₁ - f₂ eine Lösung der zugehörigen homogenen linearen Differenzgenleichung mit b(n) = 0 für alle $n \in \mathbb{N}$.

Satz 3

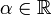Ist f₁ eine Lösung der inhomogenen linearen Differenzengleichung $\sum_{i=0}^k a_i(n)f(n+i) = b(n)$ und f₂ eine Lösung der zugehörigen homogenen linearen Differenzengleichung mit b(n) = 0 für alle $n \in \mathbb{N}$, dann ist auch f₁ + αf₂ für beliebige $\alpha \in \mathbb{R}$ eine Lösung der inhomogenen linearen Differenzengleichung.

Lösung linearer Differenzengleichungen mit konstanten Koeffizienten

Eine lineare Differenzengleichung mit konstanten Koeffizienten hat die Form $\sum_{i=0}^k a_i(n)f(n+i) = b(n)$. Alle a_i sind konstant.

Lösung der homogenen Gleichung

Mit dem Ansatz f(n) = λⁿ wird eine nichttriviale Lösung der homogenen Gleichung $\sum_{i=0}^k a_i(n)f(n+i) = b(n)$ ermittelt.

Dies führt auf die charakteristische Gleichung $\sum_{i=0}^k a_i{\lambda}^i = 0$.

Die verschiedenen Nullstellen der Gleichung ergeben dann linear unabhängige Lösungsfolgen und damit Lösungen der homogenen Gleichung.

Sind die Nullstellen nicht verschieden, so kommt die zu einer mehrfachen Nullstelle gehörende Lösungsfolge mit einem Faktor in der Lösung vor, der ein Polynom in n mit einem Grad kleiner als die Vielfachheit der Nullstelle ist.

Beispiel:

$3 \cdot x_n + 2 \cdot x_{n-1} - 5 \cdot x_{n-2} = 0$	homogene Differenzengleichung
$3 \cdot \lambda^n + 2 \cdot \lambda^{n-1} - 5 \cdot \lambda^{n-2} = 0$	Ansatz: xn = λn
$3 \cdot \lambda^2 + 2 \cdot \lambda - 5 = 0$	charakteristische Gleichung mit $\lambda_{1/2} = - \frac{1}{3} \pm \frac{4}{3}$
$x_n = c_1 \cdot \left(-\frac{5}{3}\right)^n + c_2$	Lösung der Gleichung als Linearkombination spezieller Lösungen, Konstanten können aus Anfangsbedingungen bestimmt werden.

Partikuläre Lösung

Die Bestimmung geschieht hier analog zu Differentialgleichungen.

Störfunktion b(n)	Ansatz partikuläre Lösung
Konstante	Konstante
Polynom	Polynom gleichen Grades
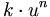
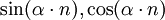
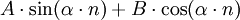
un	$k \cdot u^n$
$\sin( \alpha \cdot n) , \cos( \alpha \cdot n)$	$A \cdot \sin( \alpha \cdot n) + B \cdot \cos( \alpha \cdot n)$

Falls der Ansatz bereits eine Lösung der zugehörigen homogenen Differenzengleichung sein sollte, ist er mit n,n²,n³ zu multiplizieren, bis er eine Lösung der inhomogenen Gleichung liefert.

Beispiel

Gegeben ist eine Folge a_n mit $a_0 = 2,\quad a_1 = 5,\quad a_{n+2} = 5 \cdot a_{n+1} - 6 \cdot a_n + n$. Gesucht ist die explizite Formel. Wir suchen zuerst die allgemeine Lösung für die homogene Rekursionsgleichung.

$a_{n+2} - 5 \cdot a_{n+1} + 6 \cdot a_n = n\,$	inhomogene Rekursionsgleichung
$a_{n+2} - 5 \cdot a_{n+1} + 6 \cdot a_n = 0\,$	homogene Rekursionsgleichung, Ansatz: $a^h_n = \lambda^n$
$\lambda^{n+2} - 5 \cdot \lambda^{n+1} + 6 \cdot \lambda^n = 0\,$	Kürzen von λn, Lösungen λ = 0 verfallen.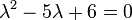
$\lambda^2 - 5\lambda + 6= 0\,$	Charakteristische Gleichung, Lösungen: λ1 = 2 und λ2 = 3
$a^h_n = c_1 \cdot 2^n + c_2 \cdot 3^n\,$	Allgemeine Lösung der homogenen Rekursionsgleichung

Nun suchen wir eine spezielle Lösung der inhomogenen Rekursionsgleichung, die partikuläre Lösung.

$a_{n+2} - 5 \cdot a_{n+1} + 6 \cdot a_n = n\,$

inhomogene Rekursionsgleichung, Ansatz: $a^p_n = x \cdot n + y$

$x \cdot (n+2) + y - 5 \cdot (x \cdot (n+1) + y) + 6 \cdot (x \cdot n + y) = n\,$

$2 \cdot x \cdot n - 3 \cdot x + 2 \cdot y = n\,$	Lösung: $x = \frac 1 2 \and y = \frac 3 4$
$a^p_n = \frac 1 2 \cdot n + \frac 3 4$	Partikuläre Lösung

Gemäß Satz 3 erhalten wir mit $a'_n = a^h_n + a^p_n = c_1 \cdot 2^n + c_2 \cdot 3^n + \frac 1 2 \cdot n + \frac 3 4$ alle Lösungen der inhomogenen Rekursionsgleichung. Nun müssen c₁ und c₂ nur noch so bestimmt werden, dass a₀ = 2 und a₁ = 5 gilt.

$c_1 \cdot 2^n + c_2 \cdot 3^n + \frac 1 2 \cdot n + \frac 3 4 = a_n$
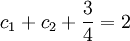
$c_1 + c_2 + \frac 3 4 = 2$	I (n = 0)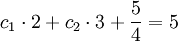
$c_1 \cdot 2 + c_2 \cdot 3 + \frac 5 4 = 5$	II (n = 1)
$c_2 - \frac 1 4 = 1$	III = II - 2 * I
$c_2 = \frac 5 4$	Durch Einsetzen in I erhalten wir außerdem $c_1 = 0\,$

Also ist $a_n = \frac 5 4 \cdot 3^n + \frac 1 2 \cdot n + \frac 3 4$ die gesuchte Formel.

Siehe auch

• Differenzengleichung
• Erzeugende Funktion
• Rekursion
• Folge
• Gewöhnliche Differentialgleichung

Literatur

• Berg, L.: Lineare Gleichungssysteme mit Bandstruktur, München-Wien: Carl Hanser, 1986
• Ian Jaques. Mathematics for Economics and Business, Fifth Edition. Prentice Hall, 2006. ISBN 0-273-70195-9. Chapter 9.1: Difference Equations, pp.551–568.