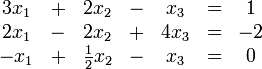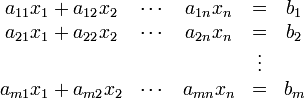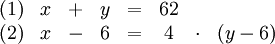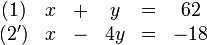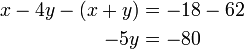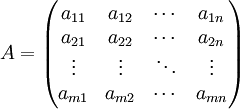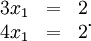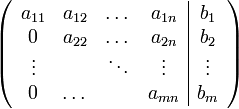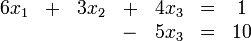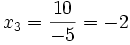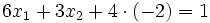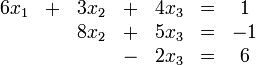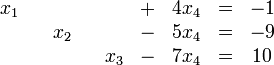Homogene Gleichung

Als lineares Gleichungssystem bezeichnet man in der linearen Algebra ein System aus linearen Gleichungen, die mehrere unbekannte Größen (Variable) enthalten.

Ein entsprechendes System für drei Unbekannte x₁, x₂, x₃ sieht beispielsweise wie folgt aus:

$\begin{matrix} 3x_1 & + & 2x_2 & - & x_3 & = & 1\\ 2x_1 & - & 2x_2 & + & 4x_3 & = & -2\\ -x_1 & + & {1 \over 2}x_2 & - & x_3 & = & 0 \end{matrix}$

Allgemein lässt sich ein lineares Gleichungssystem mit m Gleichungen und n Unbekannten immer in die folgende Form bringen:

$\begin{matrix} a_{11} x_1 + a_{12} x_2 & \cdots & a_{1n} x_n & = & b_1\\ a_{21} x_1 + a_{22} x_2 & \cdots & a_{2n} x_n & = & b_2\\ &&&\vdots&\\ a_{m1} x_1 + a_{m2} x_2 & \cdots & a_{mn} x_n & = & b_m\\ \end{matrix}$

Mit Gleichungssystemen werden Zusammenhänge modelliert, um interessierende Größen bestimmen zu können.

Man nennt das Gleichungssystem homogen, wenn alle b_i gleich 0 sind, ansonsten inhomogen. Homogene Gleichungssysteme haben stets die gültige (triviale) Lösung, dass alle Variablen 0 sind, inhomogene nie.

Beispiel

Lineare Gleichungssysteme entstehen vielfach als Modelle von praktischen Aufgabenstellungen. Beispielsweise lässt sich die Aufgabenstellung

Ein Vater und ein Sohn sind zusammen 62 Jahre alt. Vor sechs Jahren war der Vater viermal so alt wie damals der Sohn. Wie alt ist jeder?

durch das folgende lineare Gleichungssystem darstellen.

$\begin{matrix} (1) & x & + & y & = & 62 \\ (2) & x & - & 6 & = & 4 & \cdot & (y - 6) \end{matrix}$

Die Variable x repräsentiert hier das Alter des Vaters und die Variable y das des Sohnes. Das Gleichungssystem wird in einem ersten Schritt üblicherweise in eine Standardform gebracht, bei der auf der linken Seite nur Terme mit Variablen und auf der rechten Seite die reinen Zahlen stehen. Im vorliegenden Beispiel wird dazu die zweite Gleichung umgestellt.

$\begin{matrix} (1) & x & + & y & = & 62 \\ (2') & x & - & 4y & = & -18 \end{matrix}$

Um dieses Gleichungssystem zu lösen, kann auf eine Vielzahl von Lösungsverfahren zurückgegriffen werden. Beispielhaft wird hier das gaußsche Eliminationsverfahren verwendet. Um zunächst die Variable x zu eliminieren, wird die erste Gleichung von der zweiten abgezogen.

$\begin{align} x - 4y - (x + y) &= -18 - 62\\ -5y &= -80\\ \end{align}$

Die entstandene Gleichung wird nach der Variablen y aufgelöst, indem beide Seiten durch -5 geteilt werden. Man erhält das Alter y des Sohnes, der 16 Jahre alt ist. Diesen Wert für y setzt man wieder in die erste Gleichung ein.

x + 16 = 62

Indem man diese Gleichung nach der Variablen x auflöst, lässt sich das Alter des Vater berechnen, der 46 Jahre alt ist.

Matrixform

Für die Behandlung von linearen Gleichungssystemen ist es nützlich, alle Koeffizienten a_ij zu einer Matrix A, der sogenannten Koeffizientenmatrix zusammenzufassen:

$A = \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n}\\ a_{21} & a_{22} & \cdots & a_{2n}\\ \vdots & \vdots & \ddots & \vdots\\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{pmatrix}$

Des Weiteren lassen sich auch alle Unbekannten und die rechte Seite des Gleichungssystems als einspaltige Matrizen niederschreiben:

$x = \begin{pmatrix} x_1\\ x_2 \\ \vdots \\ x_n\end{pmatrix};\qquad b = \begin{pmatrix} b_1\\ b_2 \\ \vdots \\ b_m\end{pmatrix}$.

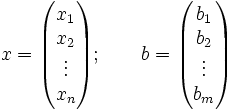Damit schreibt sich ein lineares Gleichungssystem unter Benutzung der Matrix-Vektor-Multiplikation kurz

$A \cdot x = b$.

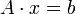Sowohl die Koeffizienten a_ij, die Unbekannten x_j als auch die b_i entstammen demselben Körper. Insbesondere gilt

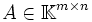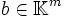$A \in \mathbb{K}^{{m}\times{n}}$, $b \in \mathbb{K}^{m}$ und $x \in \mathbb{K}^{n}$.

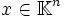Zur Festlegung eines linearen Gleichungssystems ist die Angabe der Unbekannten nicht nötig. Es genügt die Angabe der erweiterten Koeffizientenmatrix, die entsteht wenn an die Koeffizientenmatrix A eine Spalte mit der rechten Seite b des Gleichungssystems angefügt wird:

$\begin{pmatrix}A & b\end{pmatrix} = \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} & b_1 \\ a_{21} & a_{22} & \cdots & a_{2n} & b_2 \\ & & & \vdots & \\ a_{m1} & a_{m2} & \cdots & a_{mn} & b_m \end{pmatrix}$.

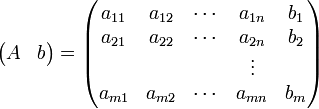Lösbarkeit

Ein Vektor x ist eine Lösung des linearen Gleichungssystems, wenn 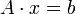$A \cdot x = b$ gilt. Ob und wie viele Lösungen ein Gleichungssystem besitzt, ist unterschiedlich. Bei linearen Gleichungssystemen treten drei Fälle auf:

• das lineare Gleichungssystem hat keine Lösung.
• das lineare Gleichungssystem hat genau eine Lösung.
• das lineare Gleichungssystem hat unendlich viele Lösungen, falls $\mathbb{K}$ kein endlicher Körper ist, ansonsten ist die Anzahl der Lösungen eine Potenz der Mächtigkeit von $\mathbb{K}$.

Dabei ist das lineare Gleichungssystem genau dann lösbar, wenn der Rang der Koeffizientenmatrix A gleich dem Rang der erweiterten Koeffizientenmatrix ist. Entspricht der Rang der (erweiterten) Koeffizientenmatrix auch noch der Anzahl der Unbekannten, so besitzt das Gleichungssystem genau eine Lösung.

Bei einem quadratischen Gleichungssystem gibt die Determinante Auskunft über die Lösbarkeit. Das Gleichungssystem ist genau dann eindeutig lösbar, wenn der Wert der Determinante der Koeffizientenmatrix ungleich null ist. Ist der Wert jedoch gleich null, hängt die Lösbarkeit von den Werten der Nebendeterminanten ab. Bei diesen wird jeweils eine Spalte der Koeffizientenmatrix durch die Spalte der rechten Seite (den Vektor b) ersetzt. Nur wenn alle Nebendeterminanten den Wert null haben, kann das System unendlich viele Lösungen haben, ansonsten ist das Gleichungssystem unlösbar.

Insbesondere Gleichungssysteme mit mehr Gleichungen als Unbekannten besitzen oft keine Lösung. Beispielsweise besitzt das folgende Gleichungssystem keine Lösung, da x₁ nicht beide Gleichungen erfüllen kann:

$\begin{matrix} 3x_1 & = & 2\\ 4x_1 & = & 2 \end{matrix}.$

Lösungen werden dann meist über die Ausgleichungsrechnung definiert und bestimmt.

Dass ein lineares Gleichungssystem unendlich viele Lösungen hat, kann nur vorkommen, wenn es weniger linear unabhängige Gleichungen als Unbekannte gibt. Beispielsweise besitzt das folgende, aus nur einer Gleichung bestehende Gleichungssystem unendlich viele Lösungen, nämlich alle Vektoren mit x₂ = 1 − x₁:

x₁ + x₂ = 1.

Lösungsmenge

Die Lösungsmenge eines linearen Gleichungssystems besteht aus allen Vektoren x, für die Ax = b erfüllt ist:

L = {x | Ax = b}

Liegt ein homogenes lineares Gleichungssystem vor, so bildet dessen Lösungsmenge einen Untervektorraum von 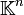$\mathbb{K}^n$. Damit sind für eine oder mehrere Lösungen 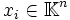$x_i \in \mathbb{K}^n$ auch deren Linearkombinationen 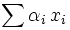$\sum\alpha_i\, x_i$ (mit beliebigen 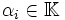$\alpha_i \in \mathbb{K}$) Lösungen des Gleichungssystems. Die Lösungsmenge heißt daher auch Lösungsraum und ist identisch mit Kern der Matrix A.

Die Lösungsmenge eines inhomogenen linearen Gleichungssystem ist ein affiner Unterraum von 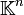$\mathbb{K}^n$. Sie hat die Form v + U, wobei U der Lösungsraum des zugehörigen homogenen Gleichungssystems ist und v eine beliebige Lösung des inhomogenen Gleichungssystems. Ein inhomogenes Gleichungssystem ist folglich genau dann eindeutig lösbar, wenn der Nullvektor die einzige Lösung („triviale Lösung“) des homogenen Gleichungssystems ist.

Die Lösungsmenge eines linearen Gleichungssystems verändert sich nicht, wenn man eine der drei elementaren Zeilenumformungen durchführt

1. Vertauschen zweier (kompletter) Zeilen
2. Multiplizieren einer Zeile mit einer von null verschiedenen Zahl
3. Addieren einer Zeile oder des Vielfachen einer Zeile zu einer anderen Zeile

Die Lösungsmenge eines quadratischen linearen Gleichungssystems verändert sich sogar nicht, wenn das Gleichungssystem mit einer regulären Matrix multipliziert wird.

Bestimmung über die erweiterte Koeffizientenmatrix

Die Form der Lösungsmenge lässt sich grundsätzlich mit Hilfe der erweiterten Koeffizientenmatrix bestimmen, indem diese mit Hilfe der elementaren Zeilenumformungen auf eine Dreiecksform gebracht wird:

$\left( \begin{array}{cccc|c} a_{11}&a_{12}&\dots&a_{1n}&b_1\\ 0&a_{22}&\dots&a_{2n}&b_2\\ \vdots&&\ddots&\vdots&\vdots\\ 0&\dots& & a_{mn}&b_m \end{array}\right)$

Die Anzahl der Lösungen lässt sich dann an der letzten Zeile ablesen. Gibt es in der letzten Zeile mindestens zwei Einträge aus der Matrix die ungleich null sind (dies impliziert weniger Gleichungen als Unbekannte), so gibt es unendlich viele Lösungen. Keine Lösungen gibt es, falls alle a_mi in der letzten Zeile null sind, b_m aber nicht. Ist a_mn als einziges a_mi in der letzten Zeile ungleich null, so ist das Gleichungssystem eindeutig lösbar. Ist a_mn gleich null und b_m auch, gibt es unendlich viele Lösungen.

Formen von Gleichungssystemen

Lineare Gleichungssysteme können in Formen vorliegen, in denen sie leicht gelöst werden können. Vielfach werden beliebige Gleichungssysteme mittels eines Algorithmus in eine entsprechende Gestalt gebracht, um anschließend eine Lösung zu finden.

quadratisch

Von einem quadratischen Gleichungssystem spricht man, wenn die Zahl der Unbekannten gleich der Zahl der Gleichungen ist. Ein Gleichungssystem dieser Form kann meistens, bei linearer Unabhängigkeit der Zeilen oder Spalten, eindeutig gelöst werden (Lösungsverfahren werden weiter unten besprochen).

Stufenform, Treppenform

In der Stufenform (auch Zeilenstufenform, Zeilennormalform, Stufengestalt, Staffelgestalt, Treppenform oder Treppennormalform) verringert sich in jeder Zeile die Zahl der Unbekannten um mindestens eine, die dann auch in den darauffolgenden Zeilen nicht mehr vorkommt. Man kann ein beliebiges Gleichungssystem durch Anwendung des gaußschen Eliminationsverfahrens in diese Form bringen.

Beispiel (die Koeffizienten von ausgelassenen Elementen sind 0):

$\begin{matrix} 6 x_1 & + & 3 x_2 & + & 4 x_3 & = & 1\\ & & & - & 5 x_3 & = & 10 \end{matrix}$

Lineare Gleichungssysteme in Stufenform können durch Rückwärtseinsetzen (Rücksubstitution) gelöst werden. Beginnend mit der letzten Zeile berechnet man dabei die Unbekannte und setzt das gewonnene Ergebnis jeweils in die darüberliegende Zeile ein um die nächste Unbekannte zu berechnen.

Lösung des obigen Beispiels:

1. Auflösen der zweiten Zeile nach x₃:

   $x_3 = \frac{10}{-5} = -2$

2. Einsetzen von x₃ in die erste Zeile:

   $6 x_1 + 3 x_2 + 4 \cdot (-2) = 1$

3. Auflösen der ersten Zeile nach x₂:

   x₂ = − 2x₁ + 3

4. Mit x₁ = t sind alle Vektoren der Form 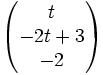$\begin{pmatrix}t \\ -2t + 3 \\ -2\end{pmatrix}$ Lösungen des Gleichungssystems.

Dreiecksform

Die Dreiecksform ist ein Sonderfall der Stufenform, bei der jede Zeile genau eine Unbekannte weniger als die vorhergehende hat. Das bedeutet, dass alle Koeffizienten a_ii der Hauptdiagonale von 0 verschieden sind. Die Dreiecksform entsteht bei Anwendung des gaußschen Eliminationsverfahrens, wenn das Gleichungssystem genau eine Lösung hat.

Beispiel (die Koeffizienten von ausgelassenen Elementen sind 0):

$\begin{matrix} 6 x_1 & + & 3 x_2 & + & 4 x_3 & = & 1\\ & & 8 x_2 & + & 5 x_3 & = & -1\\ & & & - & 2 x_3 & = & 6 \end{matrix}$

Wie lineare Gleichungssysteme in Stufenform können auch solche in Dreiecksform durch Rückwärtseinsetzen gelöst werden.

Reduzierte Stufenform

Auch die reduzierte Stufenform ist ein Sonderfall der Stufenform. Bei ihr treten die jeweils ersten Unbekannten jeder Zeile nur ein einziges Mal auf und haben den Koeffizienten 1. Die reduzierte Stufenform eines linearen Gleichungssystems ist eindeutig: es gibt also für jedes lineare Gleichungssystem genau eine reduzierte Stufenform. Man kann ein beliebiges lineares Gleichungssystem durch Anwendung des Gauß-Jordan-Algorithmus in diese Form bringen.

Beispiel (die Koeffizienten von ausgelassenen Elementen sind 0):

$\begin{matrix} x_1 & & & & & + & 4 x_4 & = & -1\\ & & x_2 & & & - & 5 x_4 & = & -9\\ & & & & x_3 & - & 7 x_4 & = & 10 \end{matrix}$

Die Lösung des linearen Gleichungssystems kann nun direkt abgelesen werden: Sofern man x₄ = t setzt und das Gleichungssystem rekursiv löst, erhält man alle Vektoren der Form ( − 4t − 1,5t − 9,7t + 10,t)^T als Lösungen.

Lösungsverfahren

Die Methoden zur Lösung von linearen Gleichungssystemen unterteilt man in iterative und direkte Verfahren. Beispiele für direkte Verfahren sind das Einsetzungsverfahren, das Gleichsetzungsverfahren und das Additionsverfahren für einfache Gleichungssysteme, sowie das auf dem Additionsverfahren basierende gaußsche Eliminationsverfahren, das ein Gleichungssystem auf Stufenform bringt. Eine Variante des Gauß-Verfahrens ist die Cholesky-Zerlegung, die nur für symmetrische, positiv definite Matrizen funktioniert. Doppelt so viel Aufwand wie das Gauß-Verfahren braucht die QR-Zerlegung, die dafür stabiler ist. Die Cramer’sche Regel verwendet Determinanten, um Formeln für die Lösung eines quadratischen linearen Gleichungssystems zu erzeugen, wenn dieses eindeutig lösbar ist. Für die numerische Berechnung ist sie auf Grund des hohen Rechenaufwands jedoch nicht geeignet.

Iterative Verfahren sind beispielsweise die zur Klasse der Splitting-Verfahren gehörenden Gauß-Seidel- und Jacobi-Verfahren. Diese konvergieren nicht für jede Matrix und sind für viele praktische Probleme sehr langsam. Modernere Verfahren sind vorkonditionierte Krylow-Unterraum-Verfahren, die insbesondere für große dünnbesetzte Matrizen sehr schnell sind.

Bei Anwendungen (z. B. Geodäsie) sind oft überbestimmte Gleichungssysteme zu lösen. Um den Messfehler von Messungen zu verringern, wird auf verschiedene Arten gemessen und es existieren mehr Messergebnisse als Unbekannte. In der Regel widersprechen sich die Gleichungen, wenn mehr Gleichungen als Unbekannte vorhanden sind. Als weitere Bedingung wird dann fast immer gestellt, dass die 2-Norm (die Addition der einzelnen Komponentenquadrate) des Residuenvektors minimal wird. Das liefert die Methode der kleinsten Quadrate.

Die Frage, wieviele arithmetische Operationen mindestens nötig sind, um ein beliebiges lineares Gleichungssystem zu lösen, ist offen. Die beste theoretische untere Schranke liefert ein praktisch nicht anwendbarer Algorithmus von Coppersmith und Winograd aus dem Jahre 1990, der ein $n \times n$-System in O(n^2,376) löst.

Literatur

• A. Meister: Numerik linearer Gleichungssysteme, 2. Auflage, Vieweg 2005, ISBN 3-528-13135-7

Weblinks

• PDF-Sammlung auf gecco.info Ausführliche Beschreibung verschiedener Lösungsmöglichkeiten von Linearen Gleichungssytemem (für Schüler, daher ohne Matrizen)
• Arndt Brünner Scripts Online-Rechner zum Lösen linearer Gleichungssysteme.
• Online-Löser für lineare Gleichungssysteme (englisch, aber unterstützt Parameter)