Linearer Potentialtopf

Dieser Artikel oder Abschnitt bedarf einer Überarbeitung. Näheres ist auf der Diskussionsseite angegeben. Hilf mit, ihn zu verbessern, und entferne anschließend diese Markierung.

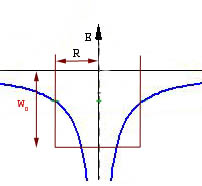
Ein Potentialtopf ist die Region um ein lokales Minimum der Potentialverteilung eines Systems. Befindet sich ein klassisches Teilchen in einem derartigen Gebiet, so kann es dieses nicht verlassen, sofern es nicht eine gewisse Gesamtenergie besitzt (Beispielsweise kann ein Mensch mit seiner Muskelkraft allein nicht genug kinetische Energie erzeugen, um das Gravitationspotential der Erde zu verlassen - Es wird eine bestimmte Energie, und damit Geschwindigkeit benötigt). Für Quantenobjekte gilt dies nicht: Ein Elementarteilchen kann die Wände eines Potentialtopfes durchtunneln (Tunneleffekt), und so den Topf verlassen, ohne die oben beschriebene kritische Gesamtenergie zu besitzen.

Anschaulich ist der Graph einer stetigen, zweidimensionalen Funktion potentieller Energie eine Oberfläche, die man sich wie die Erdoberfläche als eine Landschaft aus Hügeln und Tälern vorstellen kann. Ein Potentialtopf wäre ein Tal, das auf allen Seiten von höherem Terrain umgeben ist und das daher mit Wasser gefüllt werden könnte, ohne dass Wasser zu einem anderen, niedrigeren Minimum ablaufen würde.

Ein Potentialberg ist das Gegenteil eines Potentialtopfes, es ist die Region um ein lokales Maximum.

Mathematisch

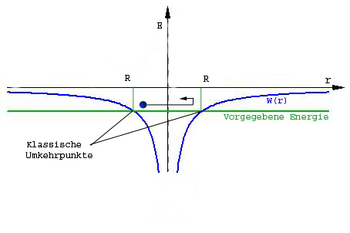
Der Umkehrpunkt ist dadurch gekennzeichnet, dass die kinetische Energie Null ist. Die gesamte Energie ist dann potentielle Energie. Im folgendem wird das H-Atom berechnet

Breite des Topfes

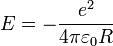$E = - \frac{e^2}{4\pi\varepsilon_0R}$ (man sieht, dass der maximale Abstand R von der Energie abhängt)

Radius:

$R = - \frac{e^2}{4\pi\varepsilon_0E}$

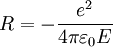
Tiefe des Topfes

Variable	Bedeutung
E	Energie
W0	Potentialtopftiefe
R	Potentialtopfbreite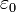
$\varepsilon_0$	elektrische Permittivität
m	Elektronenmasse

Im Potentialtopf hat das Potential einen konstanten Wert W₀. Der Potentialtopf approximiert das Coulomb-Potential am besten, wenn man W₀ so wählt, dass es die "mittlere Tiefe" des Coulomb-Potentials darstellt. Dazu berechnet man den Mittelwert 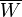$\overline{W}$ des Coulomb-Potentials über eine Kugel mit Radius R.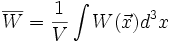

$\overline{W} = {1 \over V} \int W(\vec x)d^3x$

Das Volumen(Kugel) ist: $V={4\pi \over 3} R^3$

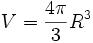
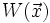$W(\vec x)$ ist: $W(\vec x) = - { e^2 \over 4\pi\varepsilon_0r}$

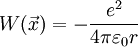
Setzt man ein: $\overline{W} = - {1 \over V} \cdot {e^2 \over 4\pi\varepsilon_0} \int\limits_{0}^{R} {1 \over r} \cdot 4 \pi r^2dr$

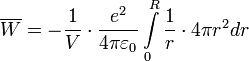
Integral auflösen: $\int\limits_{0}^{R} r dr = {1 \over 2} R^2$

$\overline{W} = - {1 \over V} \cdot {e^2 \over 4\pi\varepsilon_0} \cdot {4\pi \over V} \cdot {1 \over 2} R^2$

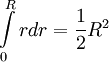
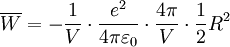
Dann 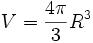$V={4\pi \over 3} R^3$ einsetzen: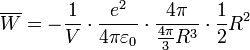

$\overline{W} = - {1 \over V} \cdot {e^2 \over 4\pi\varepsilon_0} \cdot {4\pi \over {4\pi \over 3} R^3} \cdot {1 \over 2} R^2$

vereinfacht:

$\overline{W} = - {3 \over 2} \cdot {e^2 \over 4\pi\varepsilon_0R}={3 \over 2}E$

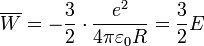
Diese Beziehung 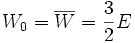$W_0=\overline{W}={3 \over 2}E$ legt die Tiefe des Potentialtopfs fest (Die Lage unterhalb des Potentialtopfs)

Dreidimensionaler Potentialtopf

$W_0={3 \over 2}E$ $, \quad R = - { e^2 \over 4\pi\varepsilon_0E}$

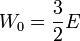
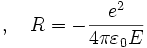
zur Vereinfachung machen wir aus der Kugel einen Würfel mit der Kantenlänge 2R

$E={h^2 \over 8m(2R)^2}(n_x^2+n_y^2+n_z^2)+W_0$

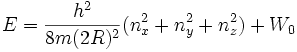
n_x = n_y = n_z = n

$E={h^2 \over 8m(2R)^2}3n^2+W_0$

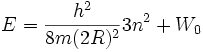
Energiewert

Nun werde W₀,R eingesetzt

$E = {3h^2 \over 32m} n^2 \cdot {(4\pi\varepsilon_0)^2E^2 \over e^4}+{3 \over 2} E$

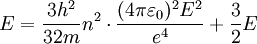
Nach E auflösen

$E = - {8 \over 3\pi^2} \cdot {me^4 \over 8h^2\varepsilon_0^2}\cdot {1 \over n^2}$

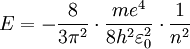
Unendlich hoher Potentialtopf

siehe Hauptartikel: Teilchen im Kasten

Eindimensionaler unendlich hoher Potentialtopf

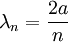$\lambda_n = \frac{2a}{n}$ mit n = 1,2,3,...

Wellenfunktion

$\Psi_n=\sqrt{\frac{2}{a}} \sin\left({2\pi \over \lambda_n}x\right)=\sqrt{\frac{2}{a}} \sin\left({n\pi \over a}x\right)$

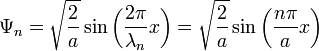
Wahrscheinlichkeitsdichte:

$\mid\Psi_n\mid^2=\frac{2}{a} \mathrm{sin}^2\left({n\pi \over a} x\right)$

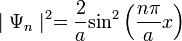
Energie Bestimmung:

$W = W_\mathrm{kin} + W_\mathrm{pot} = W_\mathrm{kin} + 0 = \frac{p^2}{2m} = \frac{h^2}{2m\lambda^2}$

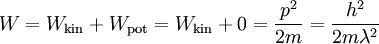
Energieniveaus eines Elektrons im Potentialtopf:

$W_n = \frac{h^2}{8ma^2} \cdot n^2 =\dfrac{\pi^2\hbar^2}{2ma^2}\cdot n^2$

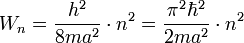
Dreidimensionaler unendlich hoher Potentialtopf

Wellenfunktion (nicht normiert)

$\Psi_{n_x,n_y,n_z}(x,y,z)=\sin\left({n_x\pi \over a}x\right)\cdot \sin\left({n_y\pi \over a}y\right) \cdot \sin\left({n_z\pi \over a}z\right)$

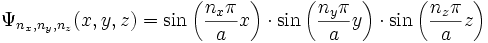
Energie

$W = {p_x^2 + p_y^2 + p_z^2 \over 2m}={h^2 \over 8ma^2}(n_x^2+n_y^2+n_z^2)$

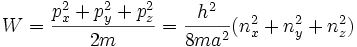
Schrödinger-Gleichung

Schrödinger-Gleichung für ein freies Teilchen in einem Potentialtopf:

$-{\hbar^2 \over 2m} {d^2 \over dx^2}\Psi(x)=E\Psi(x)$

$\Psi(x)=A\cdot \sin (kx)$

$W={\hbar^2k^2 \over 2m}= {h^2 \over 2m\lambda^2}$

$\lambda_n = \frac{2a}{n}$

$W_n = \frac{h^2}{8ma^2}\cdot n^2$

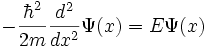
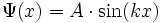
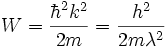
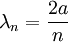
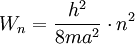
Siehe auch

• Harmonischer Oszillator (Quantenmechanik)
• Lösung des harmonischen Oszillators, des Potentialkastens und des Wasserstoffatoms