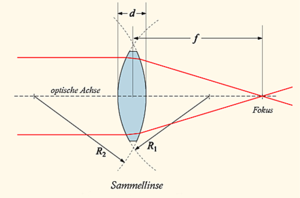
Linsenmacherformel

Als Linsenschleiferformel (auch Linsenmachergleichung) ist die Formel bekannt, mit der bei gegebenen Brechzahlen n die Radien der Kugeln errechnet werden können, deren Segmente die Linsenoberflächen bilden müssen, um eine bestimmte Brechkraft D bzw. Brennweite f zu erhalten.

f = Brennweite

Es seien

• R₁,R₂ die Kugelradien (hierbei ist zu beachten, dass die beiden Radien dann gleiche Vorzeichen haben, wenn die Mittelpunkte auf derselben Seite der Linse liegen [konvex-konkave Linse], jedoch unterschiedliche Vorzeichen, wenn die Linse bikonvex oder bikonkav ist; siehe hierzu auch: Sphärische Linsen),
• d die Dicke der Linse (gemessen in Höhe der optischen Achse),
• n₀ die Brechzahl des Mediums außerhalb der Linse,
• n die Brechzahl des Linsenmaterials,
• f die Brennweite der Linse und
• D die Brechkraft.

Für optische Systeme mit gleichen Medien in Objektraum (1) und Bildraum (2) (n₁ = n₂ = n₀) gilt allgemein:

$D = \frac{1}{f} = \frac{n - n_0}{n_0} \left( \frac{1}{R_1} - \frac{1}{R_2} +\frac{(n - n_0)d}{n R_1 R_2}\right)$

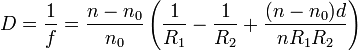
Ist unter gleichen Gegebenheiten das äußere Medium Luft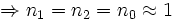 $\Rightarrow n_{1}=n_{2}=n_0 \approx 1$ gilt näherungsweise: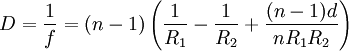

$D = \frac{1}{f} = \left( n - 1 \right) \left( \frac{1}{R_1} - \frac{1}{R_2} +\frac{( n - 1)d}{n R_1 R_2}\right)$

Weiter wird die Formel für dünne Linsen (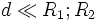$d \ll R_1;R_2$) zu

$D = \frac{1}{f} = \left( n - 1 \right) \left( \frac{1}{R_1} - \frac{1}{R_2} \right)$

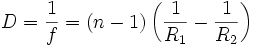
vereinfacht.