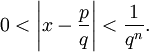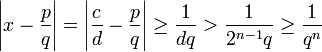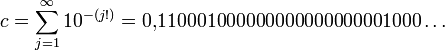Liouville — Joseph Liouville. Joseph Liouville (* 24. März 1809 in Saint Omer; † 8. September 1882 in Paris) war ein französischer Mathematiker. Er studierte in Toul und ab 1825 in Paris an der École Polytechnique, wo er zwei Jahre später, unter anderem bei … Deutsch Wikipedia
Transzendente Zahl — Eine reelle Zahl (oder allgemeiner: eine komplexe Zahl) x heißt transzendent, wenn sie nicht als Lösung einer algebraischen Gleichung beliebigen (endlichen) Grades für mit ganzzahligen oder allgemein rationalen Koeffizienten ak auftreten kann,… … Deutsch Wikipedia
Liouvillesche Zahl — Als Liouvillesche Zahl, benannt nach Joseph Liouville, bezeichnet man in der Zahlentheorie eine reelle Zahl x, welche die Bedingung erfüllt, dass für alle positiven ganzen Zahlen n ganze Zahlen p und q mit q > 1 existieren, so dass… … Deutsch Wikipedia
Eulersche Zahl — Die eulersche Zahl e = 2,718281828459045235... (nach dem Schweizer Mathematiker Leonhard Euler) ist eine irrationale und sogar transzendente reelle Zahl. Sie ist die Basis des natürlichen Logarithmus und der (natürlichen) Exponentialfunktion, die … Deutsch Wikipedia
Catalan-Zahl — Eugène Charles Catalan Die Catalan Zahlen oder catalanschen Zahlen bilden eine Folge natürlicher Zahlen, die in vielen Problemen der Kombinatorik auftritt und eine ähnlich wichtige Rolle wie die Binomialkoeffizienten oder die Fibonacci Zahlen… … Deutsch Wikipedia
Transzendente Gleichung — Eine reelle Zahl (oder allgemeiner: eine komplexe Zahl) x heißt transzendent, wenn sie nicht als Lösung einer algebraischen Gleichung beliebigen (endlichen) Grades für mit ganzzahligen oder allgemein rationalen Koeffizienten ak auftreten kann,… … Deutsch Wikipedia
Transzendente Zahlen — Eine reelle Zahl (oder allgemeiner: eine komplexe Zahl) x heißt transzendent, wenn sie nicht als Lösung einer algebraischen Gleichung beliebigen (endlichen) Grades für mit ganzzahligen oder allgemein rationalen Koeffizienten ak auftreten kann,… … Deutsch Wikipedia
Analytische Zahlentheorie — Die analytische Zahlentheorie ist ein Teilgebiet der Zahlentheorie, welche wiederum ein Teilgebiet der Mathematik ist. Die analytische Zahlentheorie verwendet Methoden der Analysis und der Funktionentheorie. Inhaltlich befasst sie sich vorwiegend … Deutsch Wikipedia
Augustin Louis Cauchy — [ogysˈtɛ̃ lwi koˈʃi] (* 21. August 1789 in Paris; † 23. Mai 1857 in Sceaux) war ein französischer Ma … Deutsch Wikipedia
Transcendence theory — In mathematics, transcendence theory is a branch of number theory that investigates transcendental numbers, in both qualitative and quantitative ways.TranscendenceThe fundamental theorem of algebra tells us that if we have a non zero polynomial… … Wikipedia
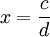 . Sei n eine positive ganze Zahl, sodass 2n − 1 > d. Wenn dann p und q ganze Zahlen sind, sodass q > 1 und
. Sei n eine positive ganze Zahl, sodass 2n − 1 > d. Wenn dann p und q ganze Zahlen sind, sodass q > 1 und 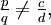 so ist
so ist