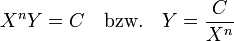Lotka's Gesetz

Lotkas Gesetz ist ein 1926 von Alfred James Lotka festgestelltes Skalengesetz, das in der Szientometrie Gebrauch findet. Es zeigt die Beziehung zwischen der Anzahl von Publikationen einer Person und der Anzahl von Personen mit einem eben so hohen Publikationsausstoß. Es wurde für die Anzahl der wissenschaftlichen Zeitschriftenartikel aufgestellt und besagt, dass die Anzahl der Personen, die n Artikel schreiben, proportional zu 1/n² ist (spätere Ergebnisse legen eher einen Exponenten von −1,7 statt −2 nahe, was nichts an der Grundaussage des Gesetzes ändert). Eine vergleichbare, aber viel einfachere Verteilung gibt die Pareto-Verteilung (80/20-Regel) vor, nach der 80 % des Informationsbedarfs von 20 % aller Quellen gedeckt werden.

Die allgemeine Formel lautet:

$X^n Y = C \quad \text{bzw.}\quad Y = \frac{C}{X^n}$

X = Anzahl der Publikationen

Y = relative Häufigkeit der Autoren mit X Publikationen

n, C = Konstanten (je nach Fachgebiet) [n ~ 2]

Beispiel

Für 100 Autoren, die in einem bestimmten Zeitraum durchschnittlich je einen Artikel schreiben, kommen:

Artikel	Autoren
10	100/102 = 1
9	100/92 ≈ 1 (1,23..)
8	100/82 ≈ 2 (1,56..)
7	100/72 ≈ 2 (2,04..)
6	100/62 ≈ 3 (2,77..)
5	100/52 = 4
4	100/42 ≈ 6 (6,25)
3	100/32 ≈ 11 (11,11..)
2	100/22 = 25
1	45 (der Rest)

Seit seiner Entdeckung wurde das unter anderem bibliometrisch, wissenschaftstheoretisch und soziologisch interessante Gesetz wiederholt bestätigt und auch in anderen Bereichen festgestellt, so z.B. bei der Anzahl der Mitarbeiter und dem Umfang ihrer Beiträge bei Open Source Projekten.

Lotkas Gesetz gilt grundsätzlich auch für die Autoren und Beiträge der Wikipedia.

Auch die Zahl der Zitierung pro Publikation nimmt im Verhältnis n^−2,5 bis n⁻³ ab.

An den Enden ist die Lotka-Verteilung etwas gebogen, da dem Publikationsaufkommen einer Person unten (1 Artikel) und oben (je nach Fall) Grenzen gesetzt sind.

Literatur

• Alfred James Lotka: The frequency distribution of scientific productivity. In: Journal of the Washington Academy of Sciences, 16, 1926, S. 317-323.
• Leo Egghe. Relations between the continuous and the discrete Lotka power function. In: Journal of the American Society for Information Science and Technology. 56, Nr. 7, 2005, S. 664-668.
• Herbert A. Simon: Models of Man, Social and National. New York 1957, S. 160
• Derek J. de Solla Price: Litte Science, Big Science. Suhrkamp, Frankfurt 1974.
• R. Rousseau: Breakdown of the robustness property of Lotka Law - the case of adjusted counts for multiauthorship attribution. In: Journal of the American Society for Information Science 43 (10): 645-647 DEC 1992.

Weblinks

• Brendan Rousseau and Ronald Rousseau: LOTKA: A program to fit a power law distribution to observed frequency data [1] [2]
• http://www.ib.hu-berlin.de/~wumsta/price52.html