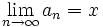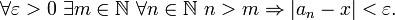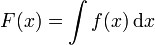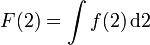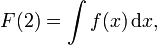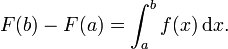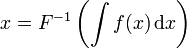Mathematische Notation

Als Notation bezeichnet man in Mathematik, Logik und Informatik die Schreibweise von Formeln und Ausdrücken mittels mathematischer Symbole. Die mathematische Notation entspricht einer Sprache, die formaler ist als viele natürliche Sprachen und dennoch einige Uneindeutigkeiten enthält, wie sie für natürliche Sprachen charakteristisch sind.

Bestandteile

Die mathematische Notation bedient sich Symbolen

• wie +, sin, 2, x für mathematische Objekte, etwa Funktionen bzw. Zahlen,
• für Zuordnungszwecke, also Klammern,
• und für den Aufbau von Schablonen.

Bei den Bezeichnungen für mathematische Objekte unterscheidet man

• Konstanten, also allgemeingültige Bezeichnungen für häufig gebrauchte Objekte wie sin, π, 0 und
• Variablen, also zum Beispiel Bezeichnungen für Objekte, die erst noch gefunden werden müssen oder über die man etwas allgemein aussagen möchte.

Die Kombination einer Funktion mit einem anderen Objekt steht für das Bild dieses Objekts unter der Abbildung durch die Funktion. So stehen cos und 0 für sich genommen für eine Funktion und eine Zahl, jedoch steht die Kombination cos0 nicht für die einzelnen Objekte, sondern für die Zahl 1. cos0 und 1 stehen also für das gleiche mathematische Objekt, die Bezeichnung mathematischer Objekte ist mithin nicht eindeutig.

Spezielle Notationen

Neben dem Zusammensetzen von Ausdrücken aus Bezeichnungen für mathematische Objekte, sind auch gewisse Schablonen weit verbreitet. Damit sind Notationen gemeint, in denen manche verwendete Symbole nicht für mathematische Objekte stehen und sich der Ausdruck nur als ganzes verstehen lässt. Beispielsweise steht in der Grenzwertschreibweise

$\lim_{n\rightarrow\infty} a_n = x$

das Unendlichkeitssymbol $\infty$ nicht für eine Zahl und der Pfeil nicht für eine mathematische Operation. Man kann diesen Ausdruck lediglich als ganzes verstehen und etwa in seine Definition überführen

$\forall \varepsilon>0 \ \exists m\in\N \ \forall n\in\N\ n>m\Rightarrow|a_n-x|<\varepsilon.$

Eine weitere derartige Notation ist für das unbestimmte Integral in Gebrauch. Würde man die Gleichung

$F(x) = \int f(x)\, {\mathrm d} x$

als Ausdruck aus mathematischen Objekten betrachten, könnte man F auf eine Zahl anwenden, zum Beispiel 2, aber

$F(2) = \int f(2) \, {\mathrm d} 2$

ergibt offensichtlich keinen Sinn. Man könnte einwenden, dass x durch das Integral gebunden wird. Dann hieße der spezialisierte Ausdruck

$F(2) = \int f(x)\, {\mathrm d} x,$

was auch nicht sinnvoll ist. Daher handelt es sich bei dieser Schreibweise ebenfalls um eine spezielle Notation, die nur als ganzes verstanden werden kann, etwa als

$F(b) - F(a) = \int_a^b f(x) \,{\mathrm d} x.$

Spezialnotationen sind problematisch, weil für sie elementare Umformungsregeln nicht anwendbar sind. Ist beispielsweise f eine umkehrbare Funktion, dann kann man die Gleichung f(x) = y äquivalent in x = f ^{− 1}(y) umformen. Bei obigem unbestimmten Integral hingegen, ergibt die Umformung

$x = F^{-1}\left(\int f(x) \,{\mathrm d} x\right)$

gar keinen Sinn.

In der Mathematik gibt es viele solche Spezialnotationen und es ist nicht klar, ob sie sich vollständig mit Ausdrücken, die aus reinen mathematischen Objekten bestehen, ersetzen lassen und ob derart abgewandelte Notationen für Menschen noch komfortabel verwendbar sind.

Grammatiken

Neben der Festlegung, welche Zeichen für die einzelnen Operatoren verwendet werden (z.B. „+“ für die Addition), ist die Festlegung der Reihenfolge von Funktionen und ihren Operanden ein wichtiger Punkt. In der heute üblichen mathematischen Notation sind viele Varianten gemischt:

Name	Beschreibung	Beispiele
Präfixnotation	Funktion vor Operanden	sin, cos, ln, f, D (Ableitung)
Postfixnotation	Funktion nach Operanden	!, ' (Ableitung)
Infixnotation	Funktion zwischen Operanden, geht nur bei zweistelligen Funktionen	+ , − , $\cdot$, :, * (Faltung), $\in$, < , $\lor$
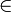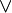
	Funktion über Operanden	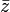$\bar{z}$ (Komplexe Konjugation), 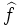$\widehat{f}$ (Fourier-Symbol), 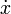$\dot{x}$ (Ableitung)
	Klammern um Operanden	$\lfloor\cdot\rfloor$, $\|\cdot\|$, $\langle\cdot,\cdot\rangle$, $\sqrt{\ \ }$
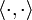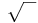
	Funktionsanwendung ohne Symbole	ab (Multiplikation), ab (Potenz)
	andere	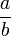$\frac{a}{b}$ (Bruch), 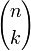$n\choose k$ (Binomialkoeffizient)

Am gebräuchlichsten ist die arithmetische Notation oder algebraische Notation. Bei ihr wird die Rechenreihenfolge durch die Wertigkeit der Operationen („Punkt- vor Strichrechnung“) bestimmt. Durch das Setzen von Klammern kann man Teilausdrücke festlegen, die zuerst berechnet werden müssen. Beispiel:

(3 + 4 + 5) · 6 · 7 + 8

Die Operatoren stehen zwischen den einzelnen Werten, es handelt sich hierbei also um eine Infixnotation.

Ein weiteres Beispiel für Infix ist die in der Logik verwendete Peano-Russell-Notation:

((p → q) ∨ (q → p))

Solche Ausdrücke können recht schnell sehr unübersichtlich werden. In den 1920ern entwickelte deshalb der polnische Logiker und Philosoph Jan Łukasiewicz die Polnische Notation, eine Präfix-Notation, die ohne Klammern auskommt. Die Operatoren werden dabei mit Großbuchstaben bezeichnet, z.B. C für die materiale Implikation (hinreichende Bedingung) und A für die Disjunktion (Alternative). In polnischer Notation schreibt man den vorgenannten logischen Term so:

ACpqCqp

Bei der Postfix-Notation schreibt man den Operator nach den zu verknüpfenden Argumenten; sie wird daher auch Umgekehrte Polnische Notation (UPN) genannt. Gelegentlich dem australischen Philosophen Charles Hamblin zugeschrieben, war sie mit hoher Wahrscheinlichkeit ebenfalls bereits Łukasiewicz bekannt. In der Logik wurde die UPN nie verwendet, sie erlangte jedoch durch Arbeiten von Hamblin einige Bedeutung in der frühen Informatik und dem frühen Compilerbau, weil sich Ausdrücke in UPN besonders leicht maschinell abarbeiten lassen. Aus demselben Grund übernahm sie die Firma Hewlett-Packard in den 60er Jahren für ihre wissenschaftlichen Taschenrechner.

Andere klammerfreie Notationen sind die Begriffsschriftnotation von Gottlob Frege, die Schreibweise des ersten prädikatenlogischen Systems überhaupt, sowie die Existential Graphs von Charles S. Peirce. Beide weichen zudem stark von den heute gebräuchlichen Notationen ab, weil es sich um graphische, zweidimensionale Schreibweisen handelt.

Untersuchung mathematischer Notation

Die mathematische Notation ist Gegenstand von Untersuchungen in folgenden Bereichen:

• Semiotik
• Geschichte der Mathematik (Florian Cajori: History of mathematical notation)
• Standardisierung Deutsches Institut für Normung (DIN-Taschenbuch 202 und 22), Internationale Organisation für Normung
• Computeralgebra (Stephen Wolfram: Mathematical Notation: Past and Future)
• Entwicklung von Programmiersprachen
• Künstliche Intelligenz: automatische Beweiser und Beweisprüfer
• Formale Begriffsanalyse und Verbandstheorie
• Mathematikdidaktik

Siehe auch

Für eine tiefergehende und vollständigere Beschreibung siehe folgende Einzelartikel:

• Zur Mehrdeutigkeit von Ausdrücken in Infix-Schreibweise: Operatorrangfolge und Operatorassoziativität
• Zu einzelnen Notationen: Polnische Notation, Umgekehrte Polnische Notation, Peano-Russell-Notation, Begriffsschriftnotation und Existential Graphs
• Zur Bedeutung und Verwendung gängiger Symbole, siehe Mathematische Symbole.