- Umgekehrte Polnische Notation
-
Die Umgekehrte Polnische Notation (kurz UPN), englisch Reverse Polish Notation (kurz RPN), auch Postfixnotation genannt, ist eine von der Polnischen Notation abgeleitete Schreibweise bzw. Eingabelogik für die Anwendung von Operationen. Bei der umgekehrten polnischen Notation werden zunächst die Operanden niedergeschrieben bzw. eingegeben und danach der darauf anzuwendende Operator.
Taschenrechner mit der Umgekehrten Polnischen Notation wie der HP 48 besitzen eine meist auffällige Enter-Taste, dafür fehlen die Klammertasten (, ) und die Gleichheitstaste =. Eine konventionelle Löschtaste zur Einleitung der Berechnung fehlt ebenfalls, da nicht mehr benötigte Ergebnisse während der Berechnungen automatisch aus dem Stapel geschoben werden. Eine modifizierte Löschtaste wird allerdings zur Beseitigung von Tippfehlern verwendet.
Inhaltsverzeichnis
Prinzip
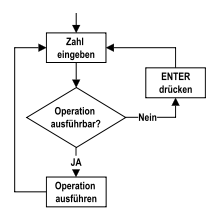
In der Informatik ist die UPN deshalb von Interesse, weil sie eine stapelbasierte Abarbeitung ermöglicht: Operanden werden beim Lesen auf den Stapel gelegt, ein Operator holt sich die Anzahl an Operanden vom Stapel (Stack), die seiner Stelligkeit entspricht, und legt das Ergebnis der Operation wieder auf dem Stapel ab. Am Ende liegt dann das Ergebnis des Terms oben auf dem Stapel. Deshalb bildet die UPN die Grundlage für stapelbasierte Programmiersprachen wie Forth, RPL, PostScript oder die Anweisungsliste im SPS-Bereich.
Es sollen 3 und 4 addiert werden. Die Operanden sind dann 3 und 4, der Operator ist „+“:
In der Schule ist die erlernte Notation die (sequenziell organisierende) Infix-Notation „3+4“. In der umgekehrten polnischen Notation wird hingegen „3 4 +“ geschrieben (zwischen 3 und 4 ist ein Leerraum, damit die Zahlenfolge von der Zahl 34 unterschieden werden kann).
Weiteres Beispiel (in der Infix-Notation): „(3+4)×5“. Bei der UPN können die Klammern entfallen, alle Operationen (hier „+“ und „ד) arbeiten mit den beiden oberen Elementen des Stapels. Das Beispiel heißt in UPN dann: „3 4 + 5 ד (zuerst wird der Klammerausdruck „3 4 +“ausgerechnet, danach die hierbei entstandene Zahl 7 mit 5 multipliziert).
Dieses Prinzip ist auch in der deutschen Sprache zu finden. Alltagssprachlich werden oft erst die Dinge genannt, mit denen man etwas tun kann („Wäsche“), und danach das, was man damit macht („waschen“). Häufig findet sich diese Struktur in Anleitungen und Rezepten, wo es auf Kürze und schnelle Verständlichkeit ankommt:
- Die Wäsche mit Seife waschen.
- Das Brot mit dem Messer schneiden.
- Mehl und Eier mischen.
Sprachlich kann man die Unterschiede der Infix-Notation „(3+4)×5“ und der UPN „3 4 + 5 ד wie folgt veranschaulichen:
- Statt „3 plus 4, mal 5“ sagt man „3 und 4 addieren und mit 5 multiplizieren“.
Bei nicht-kommutativen Operationen ist die Reihenfolge in beiden Schreibweisen identisch.
Bei Operatoren mit nur einem Operanden ist UPN auch bei (Taschen-) Rechnern sehr gebräuchlich, die sonst mit der Infix-Notation arbeiten. Beispiele dafür sind die trigonometrischen oder logarithmischen Funktionen, die bei den meisten Taschenrechnern in der Form 2 5 ln oder 2 5 sin eingegeben werden (der Operator „ln“ bzw. „sin“ wird nach dem Operanden „25“ eingegeben).
Für die Konversion zwischen den Schreibweisen lässt sich der Shunting-yard-Algorithmus verwenden.
Vorteile
 Der UPN-finanzmathematische Taschenrechner HP-12C wird seit 1981 bis heute gebaut
Der UPN-finanzmathematische Taschenrechner HP-12C wird seit 1981 bis heute gebaut
Unter Anwendern wird häufig der Vorteil der UPN zur algebraischen Notation (Infix-Notation) diskutiert.
Der augenfälligste Vorteil der UPN ist, dass sie im Allgemeinen mit einer geringeren Anzahl von Tastendrücken auskommt. Um zum Beispiel die Rechnung (1+2)×(3+4) vorzunehmen, muss man im algebraischen Modus zwölf Tasten betätigen:
- ( 1 + 2 ) × ( 3 + 4 ) =
Bei vielen Implementierungen lässt sich die Tastenfolge noch optimieren; dies ist allerdings genaugenommen kein „algebraisches Vorgehen“:
- 1 + 2 = × ( 3 + 4 =
Im UPN-Modus sind nur neun Tastendrücke erforderlich:
- 1 Enter 2 + 3 Enter 4 + ×
Es sind also drei Tasten weniger zu drücken als im algebraischen Modus; bei aufwendigeren Rechnungen ist die Ersparnis entsprechend größer.
Ein weiterer Vorteil der UPN ist es, dass die Rechnung stets schrittweise und mit sichtbaren Zwischenergebnissen ausgeführt wird; man kann die Daten also nach und nach weiterbearbeiten; allerdings zeigen auch viele algebraische Taschenrechner Zwischenergebnisse, so weit das möglich ist, zum Beispiel beim Betätigen der )-Taste den Wert des aktuellen Klammerausdrucks.
Die Verfügbarkeit von Zwischenergebnissen erleichtert es nicht nur, die Eingaben zu kontrollieren und Fehler zu identifizieren, sondern erlaubt es im Zusammenhang mit den bei UPN verfügbaren Vertauschungsoperationen innerhalb des Stapels, jedes Zwischenergebnis einfach zu speichern – etwa in Speicherregistern – und später weiterzuverarbeiten. Insbesondere lässt sich der häufig vorkommende Fall, dass ein Operand gleich nochmals benötigt wird – wie etwa in der Rechnung (a-b)/b – ohne erneute Eingabe von b rechnen; UPN-Rechner verfügen dafür über ein Register LASTX, das den letzten Operanden automatisch speichert.
Die Programmierung eines UPN-Rechners folgt normalerweise exakt der manuellen Eingabe einer Berechnung, was vor allem bei häufigen kurzen Rechenaufgaben sehr anwendungsfreundlich ist, weil keine gesonderte Programmiersprache erlernt werden muss. Bei algebraischen Taschenrechnern weicht das Programmiermodell oft (aber nicht immer) von der manuellen Formeleingabe ab.
Nachteile
Nachteil der UPN ist in erster Linie die Tatsache, dass sie häufig nicht aus dem täglichen Leben beziehungsweise der Schule vertraut ist und daher erst erlernt werden muss; hinzu kommt, dass die Vorteile erst beim intensiveren Gebrauch und vor allem bei der Arbeit mit komplizierten Formeln zu bemerken sind. Die Gewöhnung an eine der beiden Notationen kann den Umgang mit der jeweils anderen erschweren.
Umsetzung
In der Vergangenheit, insbesondere in der Frühzeit elektronischer Taschenrechner, galt als wesentlicher Vorteil der UPN, dass sie sich mit geringerem Hardwareaufwand realisieren lässt. Es ist erwiesen, dass sich beliebig komplexe mathematische Berechnungen mit einem Stapel von nur vier Einträgen ausführen lassen, dadurch lässt sich ein vollwertiger UPN-Taschenrechner mit nur vier Stapelregistern bauen. Demgegenüber muss ein algebraischer Taschenrechner für jede Klammerebene und allgemein für jedes Zwischenergebnis („Punkt- vor Strichrechnung“), das er verarbeiten soll, ein eigenes Register besitzen; in der Praxis wurden algebraische Taschenrechner mit bis zu zwölf Operandenregistern zur Speicherung von bis zu elf unvollständigen Operationen hergestellt. Mit der Leistungsfähigkeit der heutigen elektronischen Schaltkreise ist dieser theoretische Vorteil der UPN technisch nicht mehr bedeutsam, und es werden heute moderne UPN-Taschenrechner mit mehr als vier Stapelregistern und mit zusätzlichen Speicherregistern ausgestattet.
Modelle
Es gibt im Vergleich zu rein algebraischen Taschenrechnern nur wenige Taschenrechnermodelle, die auch oder ausschließlich UPN unterstützen; der einzige bekannte Hersteller, der eine größere Zahl UPN-fähiger Geräte herstellt, ist Hewlett Packard. Mit Ausnahme des seit 1981 erhältlichen reinen UPN-Taschenrechners HP-12C und einiger rein algebraischer Geräte im unteren Preisbereich unterstützen die Anfang 2007 neu auf den Markt gekommenen HP-Taschenrechner wie der HP-50g beide Eingabenotationen.
Der in Emacs integrierte Taschenrechner Calc verwendet optional die umgekehrte polnische Notation. Auf der Shell nahezu jedes Unix-Systems steht der Rechner dc zur Verfügung, der ebenfalls auf der umgekehrten polnischen Notation beruht. Auch der Rechner von Mac OS X kann optional im UPN-Betrieb genutzt werden, wobei allerdings eine falsche Implementation des Stacks die Benutzbarkeit einschränkt.
Geschichte
Die Polnische Notation (auch Präfix-Notation oder Łukasiewicz-Notation) verdankt ihren Namen dem polnischen Mathematiker Jan Łukasiewicz, der sie in den 1920er-Jahren entwickelte (eine genauere Datierung ist wohl nicht möglich[1]). Łukasiewicz stellte die polnische Notation als kompakte und klammerfreie Schreibweise für die Aussagenlogik vor.
Łukasiewicz weist selbst darauf hin,[2] dass seine Schreibweise zwar die kompakteste und die erste linear geschriebene klammerfreie Schreibweise ist, aber nicht die erste klammerfreie Schreibweise überhaupt. Der Verdienst, die Logik von der Klammer befreit zu haben, kommt Gottlob Frege mit seiner bereits 1879 veröffentlichten Begriffsschriftnotation zu.
Der gleiche Effekt der Klammerfreiheit wird erreicht, wenn der Operator nicht vor den Operanden, sondern danach steht. Diese Variante der polnischen Notation, die als „Umgekehrte Polnische Notation“ bezeichnet wird, wurde vermutlich ebenfalls bereits von Łukasiewicz gesehen. Explizit angesprochen und praktisch verwendet wurde die umgekehrte polnische Notation allerdings wohl erst in den 1950er-Jahren vom australischen Philosophen Charles Hamblin.
Einzelnachweise
- ↑ „Die ältesten Texte in den ‚Selected Works‘, in denen Łukasiewicz polnische Notation verwendet, datieren relativ spät, sind aber Präsentationen vorangehender Arbeiten, die ‚in the course of the years 1920–1930‘ (Seite 131) stattgefunden haben, also auch keine genauere Zeitangabe geben.“ (Ch. Gottschall: Logische Notationen und deren Verarbeitung auf elektronischen Rechenanlagen aus theoretischer, praktischer und historischer Sicht (Diplomarbeit), Wien 2005, S. 88)
- ↑ „On the history of the logic of propositions“, abgedruckt in: Łukasiewicz, 1970
Literatur
- Jan Łukasiewicz, L. Borkowski (Hg.): Selected Works, Warschau: PWN 1970.
- Charles L. Hamblin: Translation to and from Polish notation, The Computer Journal, Volume 5, Issue 3, Oktober 1962, S. 210–213.
Weblinks
Wikimedia Foundation.