Maximales Element

Die Begriffe maximales Element und minimales Element werden in der Mengenlehre, genauer in der Ordnungstheorie verwendet.

Ein Element einer geordneten Menge ist maximal, wenn es kein größeres gibt. Es ist minimal, wenn es kein kleineres gibt.

Für eine total geordnete Menge stimmen die Begriffe größtes Element und maximales Element überein. Ebenso stimmen kleinstes Element und minimales Element überein. Für eine partiell geordnete Menge können sie sich aber unterscheiden.

Definitionen

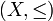$(X, \le)$ sei eine partielle Ordnung, 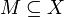$M \subseteq X$ eine Teilmenge der Grundmenge X und $x \in M$.

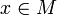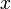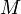
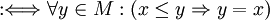
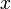$x\$ ist maximales Element von $M\$ $: \Longleftrightarrow \forall y \in M: (x \le y \Rightarrow y = x)$

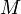
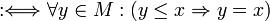
$x\$ ist minimales Element von $M\$ $: \Longleftrightarrow \forall y \in M: (y \le x \Rightarrow y = x)$

Beispiele

• M := {2, 3, 4, 6, 9, 12, 18} ist die Menge der nichttrivialen natürlichen Teiler der Zahl 36. Diese Menge ist bezüglich der Teilbarkeit partiell geordnet. Minimale Elemente sind 2 und 3, maximal sind 12 und 18. Es gibt kein kleinstes und kein größtes Element.
• Die nichtleeren Teilmengen einer gegebenen nichtleeren Menge X sind durch Inklusion partiell geordnet. Minimal in dieser Ordnung sind alle einelementigen Teilmengen {x}, maximales (und auch größtes) Element ist X selbst.
• In einem Vektorraum ist eine Basis eine (bezüglich Inklusion) maximale linear unabhängige Teilmenge.

Eigenschaften

• Jede endliche nichtleere geordnete Menge hat minimale und maximale Elemente.
• Ist x das größte Element von M, dann ist x auch das einzige maximale Element von M. Die Umkehrung gilt nicht: Auch wenn M genau ein maximales Element hat, muss M kein größtes Element haben.
• Ist x das kleinste Element von M, dann ist x auch das einzige minimale Element von M. Die Umkehrung gilt nicht: Auch wenn M genau ein minimales Element hat, muss M kein kleinstes Element haben.
• Hat jede Kette in einer nichtleeren halbgeordneten Menge eine obere Schranke, dann hat die Menge mindestens ein maximales Element. (Dies ist das Lemma von Zorn.)
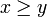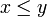• Für zwei verschiedene maximale oder zwei verschiedene minimale Elemente x und y gilt weder $x\geq y$ noch $x\leq y$. Dies lässt sich noch verallgemeinern: Die Menge aller maximalen Elemente ist eine Antikette in der Ordnung. Gleiches gilt für die Menge aller minimalen Elemente.