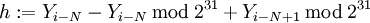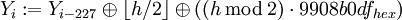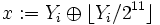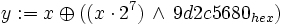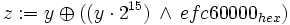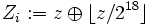Mersenne Twister

Der Mersenne-Twister ist ein Pseudozufallszahlengenerator, der 1997 von Makoto Matsumoto und Takuji Nishimura entwickelt wurde. Er ermöglicht die schnelle Erzeugung hochwertiger Sequenzen von Pseudozufallszahlen und wurde extra darauf zugeschnitten, die Probleme älterer Algorithmen zu überwinden.

Es gibt zwei Varianten dieses Algorithmus; die neuere und verbreitetere ist der Mersenne-Twister MT 19937, der hier beschrieben wird.

Eigenschaften

1. Er hat die extrem lange Periode von 2¹⁹⁹³⁷-1 (≈ 4,3·10⁶⁰⁰¹). Diese Periodenlänge erklärt auch den Namen des Algorithmus: Sie ist eine Mersenne-Primzahl, und einige Eigenschaften des Algorithmus resultieren daraus.
2. Er liefert hochgradig gleichverteilte Sequenzen (bewiesene Gleichverteilung bis zur Dimension 623, siehe unten). Daraus folgt eine extrem kleine Korrelation zwischen aufeinanderfolgenden Wertefolgen der Ausgabesequenz.
3. Er ist schneller als jeder andere bekannte (hinreichend gute) Algorithmus.
4. Alle Bits der Ausgabesequenz sind für sich gleichverteilt.

Andererseits hat er den Nachteil, auf einer großen Datenmenge von 2,5 kB (624 Wörter mit je 32 Bits) zu arbeiten. Mit den heutigen Rechnerarchitekturen mit schnellem, aber relativ kleinem Cache und langsamerem Arbeitsspeicher kann sich daraus ein Geschwindigkeitsnachteil ergeben.

Das Wort „Twister“ bezieht sich auf eine bestimmte Transformation des Algorithmus, durch die diese hochgradige Gleichverteilung sichergestellt wird. (Reine lineare Kongruenzgeneratoren können mit vertretbarem Aufwand nur fünfdimensionale Gleichverteilung garantieren.)

Eine n-dimensionale Gleichverteilung heißt: teilt man die Ausgabesequenz in Tupel von je n Zahlen, dann ist die Sequenz der n-Tupel gleichverteilt im n-dimensionalen Raum.

Im Gegensatz zu anderen Algorithmen ist der Mersenne-Twister in seiner Reinform nicht für kryptographische Anwendungen geeignet. Für viele andere Anwendungen wird er aber bereits erfolgreich verwendet.

Algorithmus

Die Werte Y₁ bis Y_N (mit N = 624) werden als Startwerte vorgegeben. Die weiteren Werte Y_i mit i > N werden folgendermaßen berechnet:

$h := Y_{i-N} - Y_{i-N} \, \bmod \, 2^{31} + Y_{i-N+1} \, \bmod \, 2^{31}$

$Y_i := Y_{i-227} \oplus \lfloor h/2 \rfloor \oplus ((h \, \bmod \, 2) \cdot 9908b0df_{hex})$

Das Symbol 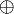$\oplus$ bezeichnet die bitweise XOR-Verknüpfung, und „hex“ steht für hexadezimal. Das Symbol 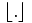$\lfloor . \rfloor$ ist die Gaußklammer und steht für den abgerundeten Wert, d. h. die größte Ganzzahl, die nicht größer als das Argument in der Klammer ist.

Um die 623-dimensionale Gleichverteilung für alle 32 Bits der Y_i sicherzustellen, werden die Y_i noch modifiziert:

$x := Y_i \oplus \lfloor Y_i / 2^{11} \rfloor$

$y := x \oplus ((x \cdot 2^7) \, \and \, 9d2c5680_{hex})$

$z := y \oplus ((y \sdot 2^{15}) \, \and \, efc60000_{hex})$

$Z_i := z \oplus \lfloor z / 2^{18} \rfloor$

Dabei steht 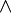$\and$ für die bitweise UND-Verknüpfung.

Die so berechneten Z_i werden als Zufallszahlen verwendet.

Initialisierung

Als Startwerte Y₁ bis Y_N wählt man im Idealfall echte Zufallszahlen, die z.B. durch einen physikalischen Zufallszahlengenerator erzeugt werden können. Es können aber auch Pseudozufallszahlen von einem anderen Generator verwendet werden. Je weniger zufällig die Startwerte sind, umso länger ist die „Aufwärmphase“, die der Mersenne-Twister braucht, bis er gute Pseudozufallszahlen ausgibt. Im Zweifelsfall sollte man ihn ca. 10000 mal aufrufen, bevor man die erzeugten Zahlen verwendet.

Es dürfen nicht alle Bits, die den Zustand des Mersenne-Twisters ausmachen, mit Null initialisiert werden, denn sonst erzeugt er immer nur Null als „Zufallszahl“. Dies sind das höchstwertige Bit in Y₁ sowie alle Bits in den übrigen Variablen Y₂ bis Y_N.

Code

Diese Berechnungen lassen sich z. B. in C-Code effizient implementieren. Die folgende Funktion berechnet immer N = 624 Wörter auf einmal, und danach werden diese aus dem Vektor y der Reihe nach ausgelesen:

unsigned mersenne_twister(void) {
  const int N = 624;
  const int M = 397;
  const unsigned A[2] = { 0, 0x9908b0df };
  const unsigned HI = 0x80000000;
  const unsigned LO = 0x7fffffff;

  static unsigned y[N];
  static int index = N+1;

  if (index >= N) {
    if (index > N) {
       // initialisiere y mit Pseudozufallszahlen:
       unsigned r = 9, s = 3402;
       for (int i=0 ; i<N ; ++i) {
          r = 509845221 * r + 3;
          s *= s + 1;
          y[i] = s + (r >> 10);
       }
    }
    unsigned h;
    for (int k=0 ; k<N-M ; ++k) {
       h = (y[k] & HI) | (y[k+1] & LO);
       y[k] = y[k+M] ^ (h >> 1) ^ A[h & 1];
    }
    for (int k=N-M ; k<N-1 ; ++k) {
       h = (y[k] & HI) | (y[k+1] & LO);
       y[k] = y[k+(M-N)] ^ (h >> 1) ^ A[h & 1];
    }
    h = (y[N-1] & HI) | (y[0] & LO);
    y[N-1] = y[M-1] ^ (h >> 1) ^ A[h & 1];
    index = 0;
  }

  unsigned e = y[index++];
  // tempering:
  e ^= (e >> 11);
  e ^= (e << 7) & 0x9d2c5680;
  e ^= (e << 15) & 0xefc60000;
  e ^= (e >> 18);
  return e;
}

TT800

Matsumoto und Nishimura entwickelten zuvor bereits einen „kleinen Bruder“ des Mersenne-Twisters mit der Bezeichnung TT800. Er arbeitet nach dem gleichen Funktionsprinzip, aber auf einer kleineren Datenmenge von nur 25 Wörtern, und sein Algorithmus ist ein wenig einfacher, weil die 64 Bits zur Berechnung des nächsten Wertes sich nicht über drei Zustands-Wörter verteilen. Seine Periodenlänge beträgt 2⁸⁰⁰-1 (≈ 6,7·10²⁴⁰).

unsigned TT800(void) {
  const int N = 25;
  const int M = 7;
  const unsigned A[2] = { 0, 0x8ebfd028 };

  static unsigned y[N];
  static int index = N+1;

  if (index >= N) {
    if (index > N) {
       unsigned r = 9, s = 3402;
       for (int i=0 ; i<N ; ++i) {
         r = 509845221 * r + 3;
         s *= s + 1;
         y[i] = s + (r >> 10);
       }
    }
    for (int k=0 ; k<N-M ; ++k)
       y[k] = y[k+M] ^ (y[k] >> 1) ^ A[y[k] & 1];
    for (int k=N-M ; k<N ; ++k)
       y[k] = y[k+(M-N)] ^ (y[k] >> 1) ^ A[y[k] & 1];
    index = 0;
  }

  unsigned e = y[index++];
  e ^= (e << 7) & 0x2b5b2500;
  e ^= (e << 15) & 0xdb8b0000;
  e ^= (e >> 16);
  return e;
}

Literatur

• M. Matsumoto and T. Nishimura: Mersenne twister: A 623-dimensionally equidistributed uniform pseudorandom number generator. ACM Trans. on Modeling and Computer Simulations, 1998.

Weblinks

• Webpräsenz des Mersenne Twister (englisch)

Arithmetische Zufallszahlengeneratoren

Kongruenzgenerator (linearer, multiplikativer, gemischt linearer, Fibonacci-Generator) | Inverser Kongruenzgenerator | Blum-Blum-Shub-Generator | Mersenne-Twister