Mersenne-Primzahl

Poststempel mit der 23. Mersenne-Primzahl, gefunden 1963 an der UIUC von Donald B. Gillies.

Eine Mersenne-Zahl ist eine Zahl der Form 2ⁿ − 1. Im Speziellen bezeichnet man mit M_n = 2ⁿ − 1 die n-te Mersenne-Zahl. Die ersten acht Mersenne-Zahlen M_n sind

0, 1, 3, 7, 15, 31, 63, 127 (Folge A000225 in OEIS).

Die Primzahlen unter den Mersenne-Zahlen werden Mersenne-Primzahlen genannt. Die ersten acht Mersenne-Primzahlen M_p sind

3, 7, 31, 127, 8191, 131071, 524287, 2147483647 (Folge A000668 in OEIS)

für die Exponenten p = 2, 3, 5, 7, 13, 17, 19, 31 (Folge A000043 in OEIS).

Die zur Basis 2 definierten Mersennezahlen zeigen sich im Dualsystem als Einserkolonnen, d.h. Zahlen, die ausschließlich aus Einsen bestehen. Die n-te Mersennezahl ist im Dualsystem eine Zahl mit n Einsen (Beispiel: M₃ = 7 = 111₂). Mersenne-Zahlen zählen im Binären zu den Zahlenpalindromen, Mersenne-Primzahlen dementsprechend zu den Primzahlpalindromen.

Ihren Namen haben diese Primzahlen von dem französischen Mönch und Priester Marin Mersenne (1588 – 1648), der im Vorwort seiner Cogitata Physico-Mathematica ^[1] behauptete, dass für p = 2, 3, 5, 7, 13, 17, 19, 31, 67, 127 und 257 M_p eine Primzahl sei.

Er irrte sich jedoch bei den Zahlen M₆₇ und M₂₅₇ und übersah die Mersenne-Primzahlen M₆₁, M₈₉ und M₁₀₇. Dass M₆₇ keine Primzahl ist, hat Édouard Lucas 1876 gezeigt, aber erst im Jahre 1903 konnte der Mathematiker Frank Nelson Cole die Primfaktoren dieser Zahl benennen. Um den Nachweis zu führen, dass M₂₅₇ keine Primzahl ist, wurde 1932 eine frühe Rechenmaschine verwendet.
Bei der Zahl M₆₇ handelt es sich möglicherweise um einen Lesefehler seitens Mersenne aus seiner Korrespondenz mit Bernard Frénicle de Bessy und Pierre de Fermat, wobei er p = 61 mit p = 67 verwechselte.

Mersenne-Zahlen kommen auch beim Mersenne-Twister vor, einem Pseudozufallszahlengenerator.

Geschichte

Mersenne-Zahlen wurden zuerst in der Antike im Zusammenhang mit vollkommenen Zahlen untersucht. Eine natürliche Zahl wird vollkommen genannt, wenn sie gleich der Summe ihrer echten Teiler ist (Beispiel: 6 = 1 + 2 + 3). Schon Euklid hatte gezeigt, dass, wenn 2ⁿ – 1 eine Primzahl ist, die Zahl 2^n-1·(2ⁿ – 1) vollkommen ist (n = 2 liefert die Zahl 6). 2000 Jahre später wurde von Euler die Umkehrung für gerade vollkommene Zahlen gezeigt: jede gerade vollkommene Zahl ist von der Form 2^n-1·(2ⁿ – 1), wobei 2ⁿ – 1 eine Primzahl ist.

Ungerade vollkommene Zahlen sind bisher nicht gefunden worden, es konnte aber auch noch nicht bewiesen werden, dass es sie nicht gibt.

Die ersten vier vollkommenen Zahlen 6, 28, 496 und 8128 waren schon in der Antike bekannt. Die Suche nach weiteren vollkommenen Zahlen motivierte die Suche nach weiteren Mersenne-Primzahlen. Die wichtigste dabei zu beachtende Eigenschaft ist die folgende:

Ist n eine zusammengesetzte Zahl, so ist auch M_n eine zusammengesetzte Zahl. Ist nämlich n ein Vielfaches von r > 1, so ist M_r > 1 und M_r Teiler von M_n.

Daraus folgt unmittelbar, dass der Exponent p einer Mersenne-Primzahl M_p = 2^p − 1 selbst eine Primzahl ist. Durch diese Eigenschaft wird die Suche nach Mersenne-Primzahlen erleichtert, da nur noch Mersenne-Zahlen mit Primzahlexponent betrachtet werden müssen.

Der Umkehrschluss ist jedoch falsch, da beispielsweise M₁₁ = 2047 = 23 · 89 keine Primzahl ist.

Mersenne-Primzahlen sind selten: bislang (2010) sind erst 47 davon gefunden worden. Da es einen besonders einfachen Primzahltest für sie gibt, sind die größten bekannten Primzahlen Mersenne-Primzahlen.

Jahr	Ereignis
bis 1536	Man glaubt, dass für alle Primzahlen p gilt, 2p–1 sei prim.
1536	Der deutsche Rechenmeister Ulrich Rieger (lat. Hudalrichus Regius) veröffentlicht in seinem Rechenbuch Utriusque Arithmetices epitome[2] als erster die fünfte vollkommene Zahl 212·(213–1) = 4096 · 8191 = 33550336 in gedruckter Form. Nachdem die Zahlen 511 und 2047 in seiner tabellarischen Übersicht nicht vorkommen, darf man annehmen, dass er 211–1 = 2047 = 23 · 89 als zusammengesetzt erkannt hat, obgleich er dies nicht extra erwähnt.
1555	Johann Scheubel veröffentlicht in seiner deutschen Übersetzung der Bücher VII-IX von Euklids Elementen die nächsten beiden vollkommenen Zahlen 216·(217–1) = 65536 · 131071 = 8589869056 und 218·(219–1) = 262144 · 524287 = 137438691328.[3] Die zweiten Faktoren sind die Mersenneschen Primzahlen M17 und M19. Allerdings hat er sowohl 211–1 = 2047 = 23 · 89, als auch 215–1 = 32767 = 7 · 31 · 151 nicht als zusammengesetzt erkannt, dafür aber 221–1 = 2097151 = 72 · 127 · 337. (Die Zerlegungen gibt er allerdings an dieser Stelle nicht an.) Er erhält in seinem Werk also fälschlicherweise neun, anstatt der korrekten sieben vollkommenen Zahlen.
1603	Pietro Cataldi (1548–1626) zeigt, dass 2p–1 prim ist für p = 17, 19. Fälschlicherweise glaubt er dies auch für p = 23, 29, 31 und 37 (ist nur für p = 31 korrekt).
1640	Fermat widerlegt Cataldi für p = 23 und p = 37: 223–1 = 47 · 178481 und 237–1 = 223 · 616318177 sind keine Primzahlen.
1644	Mersenne behauptet, 2p–1 sei prim für p = 2, 3, 5, 7, 13, 17, 19, 31, 67, 127 und 257, jedoch nicht prim für alle anderen natürlichen Zahlen kleiner als 257 (Vorwort zu seinem Werk Cogitata Physico-Mathematica). Dies ist allerdings falsch, denn 2p–1 ist prim sowohl für p = 61 (was 1883 bemerkt wird) als auch für p = 89, 107 (wird erst nach 1900 nachgewiesen).
1738	Euler widerlegt Cataldi für p = 29: 229-1 = 233 · 1103 · 2089.
1750	Euler bestätigt, dass Cataldi für p = 31 richtig lag: 231–1 ist prim.
1870	Édouard Lucas (1842–1891) formuliert die theoretischen Grundlagen für den Lucas-Lehmer-Test.
1876	Lucas bestätigt Mersenne: 2127–1 ist prim und widerspricht: 267-1 ist nicht prim, Faktoren bleiben unbekannt.
1883	Iwan Michejowitsch Perwuschin (1827–1900), ein russischer Mathematiker und orthodoxer Priester aus Perm/Russland, zeigt, dass 261–1 prim ist (Widerspruch zu Mersenne).
1903	Frank Nelson Cole benennt die Primfaktoren von 267-1 = 193707721 · 761838257287.
1911	Ralph E. Powers widerspricht Mersenne für p = 89: 2p–1 ist prim.[4]
1914	Powers widerspricht Mersenne auch für p = 107: 2p–1 ist prim. Fast gleichzeitig kommt auch E. Fauquembergue zu dieser Aussage.[5]
1930	Derrick Lehmer (1905–1991) formuliert den Lucas-Lehmer Test.
1932	Lehmer zeigt: M(149) und M(257) sind nicht prim.[6]
1934	Powers zeigt: M(241) ist nicht prim.[7]
1944	Horace S. Uhler zeigt: M(157) und M(167) sind nicht prim.[8]
1945	Uhler zeigt: M(229) ist nicht prim.[9]
1947	Uhler zeigt: M(199) ist nicht prim.[10]
1947	Der Bereich von 1 bis 257 wird vollständig überprüft. Man kennt nun die Mersenne-Primzahlen M(p) für p = 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107 und 127.[11]
1951	Beginn des Einsatzes von Computern. Die Länge der größten bekannten Primzahl steigt bis 1952 von 39 Stellen auf 687 Dezimalstellen.
1963	Donald Gillies entdeckt M(11.213) mit 3.376 Stellen.[12]
1996	Joel Armengaud und George Woltman entdecken mit GIMPS M(1.398.269) mit 420.921 Stellen.
1999	Mit M(6.972.593), die 2.098.960 Stellen hat, kennt man erstmals eine Primzahl mit mehr als 1 Million Stellen.
2004	Es wird nachgewiesen, dass M(24.036.583), eine Zahl mit 7.235.733 Stellen, prim ist.
2005	Im Februar wird vom GIMPS-Projekt die 42. Mersenne-Primzahl entdeckt: M(25.964.951) hat 7.816.230 Stellen. Ebenfalls vom GIMPS-Projekt wird im Dezember die 43. Mersenne-Primzahl entdeckt: M(30.402.457) hat 9.152.052 Stellen.
2006	Am 4. September vermeldet das GIMPS-Projekt die Entdeckung der 44. Mersenne-Primzahl M(32.582.657) mit 9.808.358 Stellen.
2008	Am 16. September werden vom GIMPS-Projekt die 45. und die 46. bekannte Mersenne-Primzahl veröffentlicht: M(37.156.667) (entdeckt am 6. September) mit 11.185.272 Stellen und M(43.112.609) (entdeckt am 23. August) mit 12.978.189 Stellen.
2009	Die 47. bekannte Mersenne-Primzahl M(42.643.801) wird vom GIMPS-Projekt am 12. April entdeckt und am 12. Juni veröffentlicht.

Teilbarkeitseigenschaften der Mersenne-Zahlen

Im Lauf ihrer langen Geschichte sind viele Ergebnisse über Mersenne-Zahlen gefunden worden. Außer der schon erwähnten grundlegenden Teilbarkeitseigenschaft (teilt r die Zahl n, so ist M_r Teiler von M_n) gibt es z. B. folgende Ergebnisse:

• Ist n eine gerade Zahl und n+1 prim, so ist n+1 ein Teiler von M_n, z. B. M₁₀ = 1023 = 3·11·31, M₁₂ = 4095 = 3²·5·7·13.

• Ist n eine ungerade Primzahl und q ein Primfaktor von M_n, so gilt q ≡ 1 (mod 2n) und q ≡ ±1 (mod 8). Beispiel: M₁₁ = 2047 = 23·89 und 23 = 2·11+1; 89 = 4·2·11+1.

• Wenn p eine Primzahl mit p ≡ 3 (mod 4) ist, dann gilt die folgende Äquivalenz: 2p+1 teilt die Mersenne-Zahl M_p genau dann, wenn 2p+1 prim ist. Beispiel: 11 ist prim und lässt einen Rest von 3 bei Division mit 4. Da 23 (als Ergebnis von 2·11+1) prim ist, folgt: 23 teilt die Mersenne-Zahl M₁₁ = 2047. Diese Aussage wurde von Leonhard Euler formuliert, aber erst später von Joseph-Louis Lagrange bewiesen (siehe auch Sophie-Germain-Primzahl).

• Ist M_p eine Primzahl > 3, dann ist M_p + 2 keine Primzahl (nämlich durch 3 teilbar). Mersenne-Primzahlen eignen sich also nicht als die kleinere Primzahl eines Primzahlzwillings.

• Ist n = 2^m (mit m > 0), so ist M_n das Produkt der Fermat-Zahlen F₀ bis F_m-1. Beispiel: M₁₆ = F₀·F₁·F₂·F₃ = 3·5·17·257.

Die Suche nach Mersenne-Primzahlen

Für die Erzielung von Primzahl-Rekorden eignen sich Mersenne-Primzahlen in mehrfacher Hinsicht besonders gut, weil (a) zusammengesetzte Exponenten unberücksichtigt bleiben können, weil diese keine Primzahlen generieren, und deshalb eine Liste der Kandidaten für den Exponent p leicht mit Primzahlgeneratoren erstellt werden kann, (b) aus dieser Liste wie oben beschrieben die Sophie-Germain-Primzahlen mit p ≡ 3 (mod 4) ausgesondert werden können (wie z. B. p = 11 → Teiler 23), (c) durch den funktionalen Zusammenhang die Größenordnung der Primzahl exponentiell – nämlich zur Basis zwei – mit dem Argument p anwächst, man also schnell sehr große Zahlen erhält, (d) mit dem nachfolgend beschriebenen Lucas-Lehmer-Test ein einfacher und effektiver Primzahltest zur Verfügung steht.

Der Lucas-Lehmer-Test

→ Hauptartikel: Lucas-Lehmer-Test

Dieser Test ist ein speziell auf Mersenne-Zahlen zugeschnittener Primzahltest, der auf Arbeiten von Édouard Lucas aus der Zeit 1870 – 1876 beruht und im Jahr 1930 von Derrick Lehmer ergänzt wurde.

Er funktioniert wie folgt:

Sei p ungerade und prim. Die Folge S(k) sei definiert durch S(1) = 4, S(k+1) = S(k)²–2.

Dann gilt: M_p = 2^p–1 ist genau dann eine Primzahl, wenn S(p–1) durch M_p teilbar ist.

GIMPS: Die große Internet-Mersenne-Primzahl-Suche

→ Hauptartikel: Great Internet Mersenne Prime Search

Bisher kennt man 47 Mersenne-Primzahlen. Mit Computerhilfe versucht man, weitere Mersenne-Primzahlen zu finden. Da es sich um sehr große Zahlen handelt – die 47. Mersenne-Primzahl hat knapp 13 Millionen Ziffern im Dezimalsystem – sind die Berechnungen (zeit- und organisations-)aufwendig. Rechenoperationen mit derart großen Zahlen werden von Computern nicht von Haus aus unterstützt. Man muss die Zahlen in großen Feldern abspeichern und die damit erforderlichen Grundrechenarten programmieren. Dies führt zu langen Programmlaufzeiten.

GIMPS (engl.: Great Internet Mersenne Prime Search) versucht daher, weltweit möglichst viele Computer an den Berechnungen zu beteiligen. Die dafür nötige Software (Prime95) wurde von George Woltman und Scott Kurowski erstellt und es gibt sie für eine Reihe von Computer-Plattformen (Windows, Unix, Linux …).

Jeder kann mitmachen, sofern er einen Rechner mit (zeitweise) freien CPU-Kapazitäten besitzt. Dazu muss man sich von der Website die Software herunterladen und dann installieren. Danach meldet man sich bei GIMPS und lässt sich eine Zahl geben, die man untersuchen soll. Wenn die Berechnungen erledigt sind (meist nach mehreren Monaten) meldet man das Ergebnis bei GIMPS zurück. Man bekommt dabei im Laufe der Computeranalyse auch Wahrscheinlichkeiten mitgeteilt: die Wahrscheinlichkeit, eine Primzahl zu finden (sehr klein, unter 1%); die Wahrscheinlichkeit, einen Faktor zu finden (größer). Diese Wahrscheinlichkeit soll die Erfolgsaussichten für das Finden einer Primzahl deutlich machen.

Liste aller bekannten Mersenne-Primzahlen

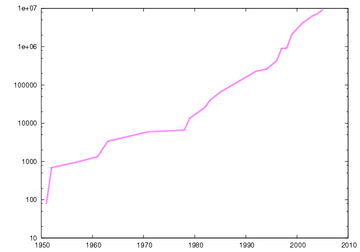Graph der Anzahl von Ziffern bei den größten bekannten Mersenne-Primzahlen im Verhältnis zum Jahr, ab 1950, der jüngsten Ära elektronischer Rechenmaschinen. Beachte: die vertikale Skala ist eine zweifach logarithmische Skala des Wertes der Mersenne-Primzahl.

Nr.	n	Anzahl Ziffern von M(n)	Jahr	Entdecker
1	2	1	-	-
2	3	1	-	-
3	5	2	-	-
4	7	3	-	-
5	13	4	1456	-
6	17	6	1555	Johann Scheubel
7	19	6	1555	Scheubel
8	31	10	1772	Leonhard Euler
9	61	19	1883	Iwan Michejowitsch Perwuschin
10	89	27	1911	Ralph E. Powers
11	107	33	1914	Powers
12	127	39	1876	Édouard Lucas
13	521	157	1952	Raphael M. Robinson
14	607	183	1952	Robinson
15	1279	386	1952	Robinson
16	2203	664	1952	Robinson
17	2281	687	1952	Robinson
18	3217	969	1957	Hans Riesel
19	4253	1281	1961	Alexander Hurwitz
20	4423	1332	1961	Hurwitz
21	9689	2917	1963	Donald B. Gillies
22	9941	2993	1963	Gillies
23	11.213	3376	1963	Gillies
24	19.937	6002	1971	Bryant Tuckerman
25	21.701	6533	1978	Landon Curt Noll, Laura Nickel
26	23.209	6987	1979	Noll
27	44.497	13.395	1979	David Slowinski, Harry Nelson
28	86.243	25.962	1982	Slowinski
29	110.503	33.265	1988	Walter Colquitt, Luther Welsh Jr.
30	132.049	39.751	1983	Slowinski
31	216.091	65.050	1985	Slowinski
32	756.839	227.832	1992	Slowinski, Paul Gage
33	859.433	258.716	1994	Slowinski, Paul Gage
34	1.257.787	378.632	1996	Slowinski, Paul Gage
35	1.398.269	420.921	1996	GIMPS / Joel Armengaud
36	2.976.221	895.932	1997	GIMPS / Gordon Spence
37	3.021.377	909.526	1998	GIMPS / Roland Clarkson
38	6.972.593	2.098.960	1999	GIMPS / Nayan Hajratwala
39	13.466.917	4.053.946	2001	GIMPS / Michael Cameron
40	20.996.011	6.320.430	2003	GIMPS / Michael Shafer
41?	24.036.583	7.235.733	2004	GIMPS / Josh Findley
42?	25.964.951	7.816.230	2005	GIMPS / Martin Nowak
43?	30.402.457	9.152.052	2005	GIMPS / Curtis Cooper, Steven Boone
44?	32.582.657	9.808.358	2006	GIMPS / Curtis Cooper, Steven Boone
45?	37.156.667	11.185.272	2008	GIMPS / Hans-Michael Elvenich
46?	42.643.801	12.837.064	2009	GIMPS / Odd M. Strindmo
47?	43.112.609	12.978.189	2008	GIMPS / Edson Smith

Bisher (Stand: 15. Juli 2010) ist unbekannt, ob es zwischen n=20.996.011 und n=43.112.609 neben den sieben bekannten Mersenne-Primzahlen noch weitere gibt; deshalb ist die Nummerierung ab Nr. 41 noch ungewiss (und mit einem '?' versehen).

Offene Fragen

Wie so oft in der Zahlentheorie gibt es auch zu Mersenne-Zahlen ungelöste Probleme, die sehr einfach zu formulieren sind:

• Gibt es unendlich viele Mersenne-Primzahlen? Man vermutet aufgrund von plausiblen Heuristiken, dass es etwa c·ln(x) viele Mersenne-Primzahlen M_p gibt mit p < x (für eine positive Konstante c). Trifft dies zu, so gibt es tatsächlich unendlich viele Mersenne-Primzahlen.

• Umgekehrt: gibt es unendlich viele Mersenne-Zahlen M_p mit p prim, die keine Primzahlen sind? Auch hier vermutet man als Antwort ja. Dies würde zum Beispiel aus der Vermutung, dass es unendlich viele Sophie-Germain-Primzahlen gibt, die kongruent 3 modulo 4 sind, folgen.

• Sind alle Mersenne-Zahlen M_p mit p prim quadratfrei, d. h. kommt in der Primfaktorzerlegung der Zahl jeder Primfaktor genau einmal vor? Man konnte bisher noch nicht einmal beweisen, dass dies für unendlich viele Mersenne-Zahlen gilt.

• Gilt die „neue Mersenne-Vermutung“? Die Folge von Mersenne-Primzahlen, die Mersenne angab, lässt vermuten, dass er meinte, dass eine Mersenne-Zahl M_p mit p prim genau dann prim ist, wenn p=2^k±1 oder p=4^k±3. Da diese Aussage nicht gilt, stellten P. Bateman, J. Selfridge und S. Wagstaff die neue Mersenne-Vermutung auf.

Diese besagt, dass aus zwei der folgenden drei Aussagen bereits die dritte folgt:

1. n = 2^k ± 1 oder n = 4^k ± 3,
2. 2ⁿ – 1 ist eine (Mersenne) Primzahl,
3. (2ⁿ+1)/3 ist eine Primzahl.

Siehe hierzu auch: die neue Mersenne-Vermutung (engl.)

• Sind alle Glieder der Folge C(0) = 2, C(k+1) = 2^C(k) – 1 Primzahlen? Die stärkere Vermutung, dass alle Zahlen M_Mp Primzahlen sind, für die M_p eine Primzahl ist, konnte inzwischen für p = 13 widerlegt werden. Diese letzteren Zahlen nennt man doppelte Mersenne-Zahlen. Auch hier ist noch nicht bekannt, ob es unendlich viele Primzahlen darunter gibt.

Einzelnachweise

1. ↑ Marin Mersenne: Cogitata Physico-Mathematica. In quibus tam naturae quàm artis effectus admirandi certissimis demonstrationibus explicantur. Paris: Bertier, 1644, Praefatio generalis, Nr. XIX.
2. ↑ Hudalrichus Regius: Vtrivsque Arithmetices epitome ex uarijs authoribus concinnata. Straßburg: Bartholomäus Grüninger, 1536, S. VIIIv-IXv, Kap. 6 (De perfecto [Über die vollkommenen Zahlen]).
3. ↑ Johann Scheubel: Das sibend, acht vnd neunt buch, des hochberümbten Mathematici Euclidis Megarensis, in welchen der operationen vnnd regulen aller gemainer rechnung, vrsach grund vnd fundament, angezaigt wirt, zu gefallen allen den, so die kunst der Rechnung liebhaben [...] auß dem latein ins teütsch gebracht, vnnd mit gemainen exemplen also illustrirt vnnd an tag geben, das sy ein yeder gemainer Rechner leichtlich verstehn, vnnd ime nutz machen kan. Augsburg: Valentin Ottmar, 1555, S. CCXXXI-CXXXIIII (Euklid IX, 36), hier S. CCXXXIII.
4. ↑ R. E. Powers: The Tenth Perfect Number. In: American Mathematical Monthly 18 (1911), Nr. 11, S. 195–197.
5. ↑ R. E. Powers: A Mersenne prime. In: Bulletin of the American Mathematical Society 20 (1914), S. 531; R. E. Powers: Certain composite Mersenne's numbers. In: Proceedings of the London Mathematical Society 15 (1916), Nr. 2, S. xxii; E. Fauquembergue: Nombres de Mersenne. In: Sphinx-Œdipe 9 (1914), S. 103-105; 15 (1920), S. 17-18. Vgl. Chris K. Caldwell: M₁₀₇: Fauquembergue or Powers?
6. ↑ D. H. Lehmer: Note on Mersenne Numbers. In: Bulletin of the American Mathematical Society 38 (1932), S. 383–384.
7. ↑ R. E. Powers: Note on a Mersenne Number. In: Bulletin of the American Mathematical Society 40 (1934), S. 883.
8. ↑ H. S. Uhler: A New Result Concerning a Mersenne Number. In: Mathematical Tables and other Aids to Computation 1 (1944), S. 333, 404. Vgl. Charles B. Barker: Proof that the Mersenne Number M167 is Composite. In: Bulletin of the American Mathematical Society 51, 1945, p. 389; H. S. Uhler: Note on the Mersenne Numbers M157 and M167. In: Bulletin of the American Mathematical Society 52 (1946), S. 178.
9. ↑ H. S. Uhler: A New Result Concerning a Mersenne Number. In: Mathematical Tables and other Aids to Computation 2 (1945), S. 94.
10. ↑ H. S. Uhler: On Mersenne's Number M199 and Lucas's Sequences. In: Bulletin of the American Mathematical Society 53 (1947), S. 163–164.
11. ↑ Vgl. H. S. Uhler: On All of Mersenne's Numbers Particularly M₁₉₃. In: Proceedings of the National Academy of Sciences of the United States of America 34 (1948), S. 102–103; H. S. Uhler: On Mersenne's Number M227 and Cognate Data. In: Bulletin of the American Mathematical Society 54 (1948), Nr. 4, S. 378–380; R. C. Archibald: Mersenne Numbers. In: Mathematical Tables and other Aids to Computation 3 (1949), S. 398.
12. ↑ Donald B. Gillies: Three New Mersenne Primes and a Statistical Theory. In: Mathematics of Computation 18 (1964), S. 93–97. Vgl. Bryant Tuckerman: Corrections. In: Mathematics of Computation 31 (1977), S. 1051.

Literatur

• Paulo Ribenboim: The new book of prime number records. 3rd edition. Springer, New York NY u. a. 1996, ISBN 0-387-94457-5 (Deutsch: Die Welt der Primzahlen. Geheimnisse und Rekorde. Auf den neuesten Stand gebracht von Wilfrid Keller. 2. vollständig überarbeitete und aktualisierte Auflage. Springer, Berlin u. a. 2011, ISBN 978-3-642-18078-1 (Springer-Lehrbuch)).

Weblinks

 Wiktionary: Mersenne-Primzahl – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

• Prime Mersenne Numbers – History, Theorems and Lists (englisch)
• Great Internet Mersenne Prime Search (GIMPS): englisch und deutsch
• Mersenne Primzahlen Bibliografie mit Links auf die Original-Veröffentlichungen (engl.)
• Wie eine neue Mersenne Primzahl entdeckt wurde – dpa-Hintergrundbericht in der taz
• Eric W. Weisstein: Mersenne-Primzahlen. In: MathWorld. (englisch)
• mprint5 – schnelle Berechnung der Mersenne-Primzahlen von dem Finnen Mikko Tommila
• Wiki über Mersenne-Primzahlen und deren Suche (engl.)