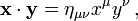Minkowski-Welt

Der Minkowski-Raum, benannt nach Hermann Minkowski, ist ein vierdimensionaler Raum, in dem sich die Relativitätstheorie elegant formulieren lässt. Minkowski führte ihn im Jahre 1907 zur Beschreibung der speziellen Relativitätstheorie ein. Er wird auch als Minkowski-Welt bezeichnet.

Drei seiner Koordinaten sind die des Euklidschen Raums; dazu kommt eine vierte Koordinate für die Zeit.

Der Minkowski-Raum ist ein reeller Vektorraum, aber kein Innenproduktraum, denn seine Bilinearform ist nicht positiv definit sondern kann auch negative Werte annehmen. Es hat die Form

$\mathbf{x\cdot y} = -x_0 y_0 + x_1 y_1 + x_2 y_2 + x_3 y_3$,

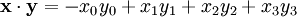wobei x₀=ct unter Verwendung der Lichtgeschwindigkeit c aus der Zeitkoordinate t hervorgeht. Statt der Signatur (-,+,+,+) wurde, vor allem in der älteren Literatur, oft auch die umgekehrte Signatur (+,-,-,-) gewählt; die Zeit wurde zuweilen als vierte statt als nullte Koordinate geführt. In der allgemeinen Relativitätstheorie wird die letztgenannte Signatur heute am häufigsten verwendet.

Alternativ kann man das innere Produkt auch als Wirkung des metrischen Tensors η_μν auffassen:

$\mathbf{x\cdot y} = \eta_{\mu\nu}x^\mu y^\nu\,,$

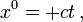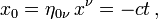
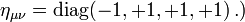indem man kontravariante und kovariante Vektorkomponenten unterscheidet ( z. B. $x^0=+ct\,,$ aber $x_0=\eta_{0\nu}\,x^\nu =-ct\,,$ $\eta_{\mu \nu}={\rm diag} (-1,+1,+1,+1)\,.)$ Dieser Formalismus eignet sich zur Verallgemeinerung in der allgemeinen Relativitätstheorie.

Weniger ausbaufähig ist eine andere, in manchen älteren, einführenden Lehrbüchern verwandte Notation: Man kann die gemischte Signatur des inneren Produkts durch Verwendung einer imaginären Zeitachse vermeiden: x₄=ict. Dies ergibt als Hauptvorteil, dass man nicht zwischen kontravarianten und kovarianten Komponenten unterscheiden muss, sondern wie in der üblichen, elementaren Vektorrechnung arbeitet. Hierbei fasst man den Minkowski-Raum formal als einen komplexen Innenproduktraum auf.

Aber auch ohne diesen Trick kann man zeigen, dass ein reeller Minkowski-Raum mit gemischter Signatur die wesentlichen Eigenschaften eines Innenproduktraums besitzt.

Für eine detailliertere Erläuterung des Minkowski-Raums siehe Lorentz-Transformation und Minkowski-Raum

Literatur

• Francesco Catoni: The mathematics of Minkowski space-time. Birkhäuser, Basel 2008, ISBN 978-3-7643-8613-9
• John W. Schutz: Independent axioms for Minkowski space-time. Longman, Harlow 1997, ISBN 0-582-31760-6
• Anthony C. Thompson: Minkowski geometry. Cambridge Univ. Press, Cambridge 1996, ISBN 0-521-40472-X

Weblinks