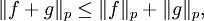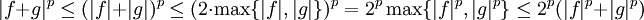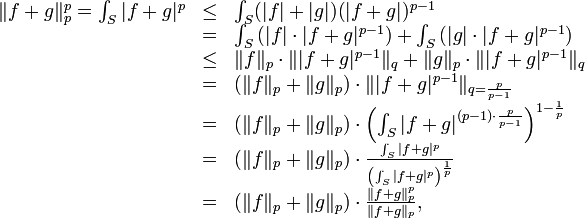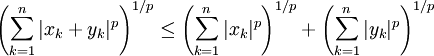Minkowski-Ungleichung — Die Minkowski Ungleichung (nach Hermann Minkowski) ist eine Aussage der Funktionalanalysis. Sie besagt, dass die Dreiecksungleichung in den Lp Räumen gilt. Inhaltsverzeichnis 1 Formulierung 2 Beweis 3 Spezialfall … Deutsch Wikipedia
Minkowski — ist der Familienname folgender Personen: Eugène Minkowski (1885–1972), russisch französischer Psychiater Hermann Minkowski (1864–1909), deutscher Mathematiker und Physiker Marc Minkowski (* 1962), französischer Dirigent Mieczyslaw Minkowski… … Deutsch Wikipedia
Minkowski-Kompaktum — Der Banach Mazur Abstand, benannt nach Stefan Banach und Stanisław Mazur, ist ein Begriff aus der mathematischen Theorie der Banachräume. Er definiert einen Abstand zwischen zwei isomorphen normierten Räumen und wird besonders für endlich… … Deutsch Wikipedia
Minkowski’s inequality — Minkovskio nelygybė statusas T sritis fizika atitikmenys: angl. Minkowski’s inequality vok. Minkowskische Ungleichung, f rus. неравенство Минковского, n pranc. inégalité de Minkowski, f … Fizikos terminų žodynas
Hölder-Ungleichung — In der mathematischen Analysis gehört die höldersche Ungleichung, benannt nach Otto Hölder, zusammen mit der Minkowski Ungleichung und der jensenschen Ungleichung zu den fundamentalen Ungleichungen für Lp Räume. Inhaltsverzeichnis 1 Aussage 1.1… … Deutsch Wikipedia
Höldersche Ungleichung — In der mathematischen Analysis gehört die höldersche Ungleichung, benannt nach Otto Hölder, zusammen mit der Minkowski Ungleichung und der jensenschen Ungleichung zu den fundamentalen Ungleichungen für Lp Räume. Inhaltsverzeichnis 1 Formulierung… … Deutsch Wikipedia
Hermann Minkowski — (* 22. Juni 1864 in Aleksotas, damals Russland (heute Kaunas, Litauen); † 12. Januar 1909 in Göttingen) war ein deutscher Mathematiker und Physike … Deutsch Wikipedia
Minkowskische Ungleichung — Minkovskio nelygybė statusas T sritis fizika atitikmenys: angl. Minkowski’s inequality vok. Minkowskische Ungleichung, f rus. неравенство Минковского, n pranc. inégalité de Minkowski, f … Fizikos terminų žodynas
inégalité de Minkowski — Minkovskio nelygybė statusas T sritis fizika atitikmenys: angl. Minkowski’s inequality vok. Minkowskische Ungleichung, f rus. неравенство Минковского, n pranc. inégalité de Minkowski, f … Fizikos terminų žodynas
Gemittelt — Mittelwerte treten in der Mathematik und insbesondere in der Statistik in inhaltlich unterschiedlichen Kontexten auf. In der Statistik ist ein Mittelwert ein sog. Lageparameter (Überbegriff Parameter (Statistik)), also ein aggregierender… … Deutsch Wikipedia
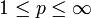 sowie
sowie 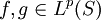 . Dann folgt
. Dann folgt 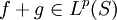 , und es gilt
, und es gilt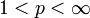 genau dann vorliegt, wenn f und g positiv linear abhängig sind (d.h. es gibt
genau dann vorliegt, wenn f und g positiv linear abhängig sind (d.h. es gibt 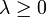 mit
mit 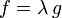 oder
oder 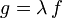 ).
).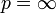 trivial. Es sei daher
trivial. Es sei daher 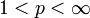 . Wegen
. Wegen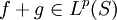 .
.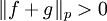 . Nach der hölderschen Ungleichung gilt
. Nach der hölderschen Ungleichung gilt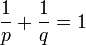 . Dies impliziert die Minkowski-Ungleichung nach Multiplikation beider Seiten mit
. Dies impliziert die Minkowski-Ungleichung nach Multiplikation beider Seiten mit 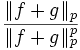 .
.
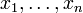 ,
, 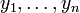 .
.