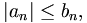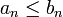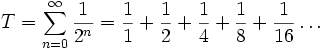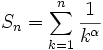- Minoranten-Kriterium
-
Das Majorantenkriterium ist ein mathematisches Konvergenzkriterium, also Mittel zur Entscheidung, ob eine unendliche Reihe konvergiert oder divergiert.
Inhaltsverzeichnis
Definition
Sei eine unendliche Reihe
mit reellen oder komplexen Summanden an gegeben. Gibt es nun eine konvergente unendliche Reihe
mit nichtnegativen reellen Summanden bn und gilt für alle n:
dann ist die Reihe S absolut konvergent. Man sagt, die Reihe S wird von T majorisiert oder T ist die Majorante von S.
Kehrt man diesen Schluss um, erhält man das Minorantenkriterium: Sind S und T Reihen mit nichtnegativen reellen Summanden an bzw. bn, und gilt
für fast alle n, dann folgt: Ist S divergent, dann ist auch T divergent.
Beweis
Konvergiert die Reihe
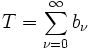 , dann gibt es zu jedem
, dann gibt es zu jedem  ein
ein 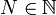 , so dass
, so dass 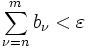 für alle
für alle 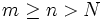 gilt (Cauchykriterium).
gilt (Cauchykriterium).Aus
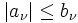 folgt
folgt 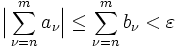 . Daraus folgt die (absolute!) Konvergenz von
. Daraus folgt die (absolute!) Konvergenz von 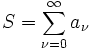 nach dem Cauchykriterium.
nach dem Cauchykriterium.Beispiel
ist konvergent. Wegen
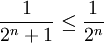 konvergiert somit auch die Reihe
konvergiert somit auch die Reihe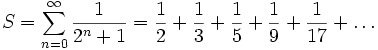 .
.
Anwendungen
Das Majorantenkriterium wird auch als allgemeinste Form eines Vergleichskriteriums 1. Art bezeichnet, alle weiteren ergeben sich durch das Einsetzen konkreter Reihen für
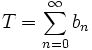 . Am prominentesten sind dabei das Wurzelkriterium und das Quotientenkriterium, in welchen die geometrische Reihe als Vergleichsreihe gewählt wird.
. Am prominentesten sind dabei das Wurzelkriterium und das Quotientenkriterium, in welchen die geometrische Reihe als Vergleichsreihe gewählt wird.
Ebenfalls lässt sich aus dem Majoranten- bzw. Minorantenkriterium das Cauchysche Verdichtungskriterium herleiten, mit dem sich beispielsweise zeigen lässt, dass die harmonische Reihekonvergent für α > 1 und divergent für
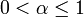 ist.
ist.Das Majorantenkriterium kann auf den Fall normierter Vektorräume ausgedehnt werden, es besagt dann, dass falls
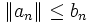 für fast alle n gilt, die Partialsummenfolge von
für fast alle n gilt, die Partialsummenfolge von 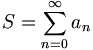 eine Cauchy-Folge ist. Ist der Raum vollständig, d.h. ein Banachraum, so konvergiert S, falls T konvergiert. Insbesondere folgt daraus der Fixpunktsatz von Banach, der in vielen konstruktiven Sätzen der Analysis benutzt wird.
eine Cauchy-Folge ist. Ist der Raum vollständig, d.h. ein Banachraum, so konvergiert S, falls T konvergiert. Insbesondere folgt daraus der Fixpunktsatz von Banach, der in vielen konstruktiven Sätzen der Analysis benutzt wird.Literatur
- Otto Forster: Analysis 1. Differential- und Integralrechnung einer Veränderlichen. 8. Aufl. Vieweg-Verlag, 2006. ISBN 3-8348-0088-0
Wikimedia Foundation.