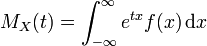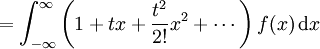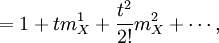- Momentenerzeugende Funktion
-
Mit der Momenterzeugenden Funktion kann das k-te Moment der Wahrscheinlichkeitsverteilung einer Zufallsvariablen ermittelt werden. In der Wahrscheinlichkeitstheorie ist die momenterzeugende Funktion einer Zufallsvariablen X definiert durch
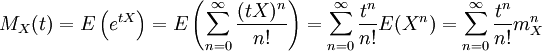 ,
,
falls deren Erwartungswerte E(Xn) existieren. Dabei sind
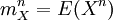 die Momente einer Wahrscheinlichkeitsverteilung.
die Momente einer Wahrscheinlichkeitsverteilung.Inhaltsverzeichnis
Für stetige Wahrscheinlichkeitsverteilung
Falls X eine stetige Wahrscheinlichkeitsdichte f(x) hat, dann ist die momenterzeugende Funktion durch
gegeben, wobei mi das i-te Moment ist. Der Ausdruck MX( − t) ist also gerade die zweiseitige Laplacetransformation des durch X festgelegten Wahrscheinlichkeitsmaßes.
Ursprung des Begriffs der momenterzeugenden Funktion
Die Bezeichnung momenterzeugend bezieht sich darauf, dass die k-te Ableitung von MX im Punkt 0 (Null) gleich dem k-ten Moment der Zufallsvariablen X ist:
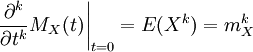 .
.
Durch die Angabe aller nicht verschwindenden Momente ist jede Wahrscheinlichkeitsverteilung vollständig festgelegt.
Verallgemeinerung auf l Zufallsvariablen
Für l Zufallsvariablen
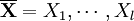 lässt sich die momenterzeugende Funktion wie folgt erweitern:
lässt sich die momenterzeugende Funktion wie folgt erweitern: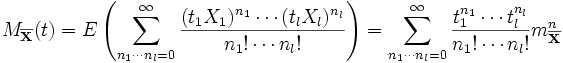 .
.
Bemerkungen
Zusammenhang mit der charakteristische Funktion
Die momenterzeugende Funktion steht in engem Zusammenhang mit der charakteristischen Funktion
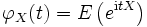 , die im wesentlichen die Inverse der Fourier-Transformierten des Wahrscheinlichkeitsmaßes darstellt.
, die im wesentlichen die Inverse der Fourier-Transformierten des Wahrscheinlichkeitsmaßes darstellt.Weitere erzeugende Funktionen
Zu den weiteren erzeugenden Funktionen zählt man die charakteristische Funktion, die wahrscheinlichkeitserzeugende Funktion und die kumulantenerzeugende Funktion als Logarithmus der momenterzeugenden Funktion.
Eindeutigkeitseigenschaft[1]
Ist die momenterzeugende Funktion einer Zufallsgröße X in einer Umgebung von 0 endlich, so bestimmt sie die Verteilung von X eindeutig. Formal bedeutet das:
Seien X und Y zwei Zufallsgrößen mit momenterzeugenden Funktionen MX und MY derart, dass es ein
 gibt mit
gibt mit 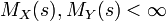 für alle
für alle 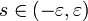 . Dann gilt PX = PY genau dann, wenn MX(s) = MY(s) für alle
. Dann gilt PX = PY genau dann, wenn MX(s) = MY(s) für alle 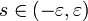 gilt.
gilt.Beispiele
Normalverteilung
Die Momenterzeugende Funktion einer normalverteilten Zufallsgröße
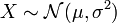 ist
ist 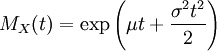 .
.Exponentialverteilung
Die Momenterzeugende Funktion einer exponentialverteilten Zufallsgröße mit Parameter λ ist
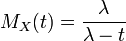
Einzelnachweise
- ↑ The Annals of Mathematical Statistics: J. H. Curtiss: A Note on the Theory of Moment Generating Functions , 16. Oktober 2008
Wikimedia Foundation.