Mutation von binären Zahlen

Die Artikel Evolutionsstrategie, Evolutionärer Algorithmus und Genetischer Algorithmus überschneiden sich thematisch. Hilf mit, die Artikel besser voneinander abzugrenzen oder zu vereinigen. Beteilige dich dazu an der Diskussion über diese Überschneidungen. Bitte entferne diesen Baustein erst nach vollständiger Abarbeitung der Redundanz. Sdo 23:29, 1. Jul. 2008 (CEST)

Genetische Algorithmen (GA) sind Algorithmen, die auch nicht analytisch lösbare Probleme behandeln können, indem sie wiederholt verschiedene „Lösungsvorschläge“ generieren, dabei verändern sowie miteinander kombinieren und einer Auslese unterziehen, so dass diese Lösungsvorschläge den gestellten Anforderungen immer besser entsprechen.

Genauer sind GA heuristische Optimierungsverfahren und gehören zu den Evolutionären Algorithmen. Sie werden vor allem für Probleme eingesetzt, für die eine geschlossene Lösung nicht oder nicht effizient berechnet werden kann, und stehen in Konkurrenz zu klassischen Suchstrategien wie dem A*-Algorithmus, der Tabu-Suche oder dem Gradientenverfahren.

Definition

Die Grundidee genetischer Algorithmen ist, ähnlich der biologischen Evolution, eine Menge (Population) von Lösungskandidaten (Individuen) zufällig zu erzeugen und diejenigen auszuwählen, die einem bestimmten Gütekriterium am besten entsprechen (Auslese). Deren Eigenschaften (Parameterwerte) werden dann leicht verändert (Mutation) und miteinander kombiniert (Rekombination), um eine neue Population von Lösungskandidaten (eine neue Generation) zu erzeugen. Auf diese wird wiederum die Auslese und Rekombination angewandt. Das wird viele Male wiederholt.

Im Gegensatz zur Genetischen Programmierung ist das Verfahren der Genetischen Algorithmen recht unflexibel, da meist nur die Parameter einer Gleichung oder eines in anderer Form vorgegebenen strukturierten Lösungsansatzes optimiert werden, anstatt jedes Individuum als eigenständiges Programm zu interpretieren.

Einige Anwendungsgebiete

• Optimierung
  • Finden des globalen Maximums/Minimums einer Funktion mehrerer Veränderlicher
  • Einstellen des Schwellenpotentialvektors sowie der Netztopologie von Neuronalen Netzen
• Genetische Programmierung zum Zwecke der automatischen Generierung von Computerprogrammen oder anderen Algorithmen, beispielsweise zur Planung von Bewegungsabläufen in Robotern
• Konstruktion von komplexen Bauteilen oder ganzen Systemen. Bisherige Anwendung im Brückenbau. GA dienen hier der Optimierung von Lage, Form und Gewicht der einzelnen Brückenbestandteile. Ähnliche Anwendung auch in der Konstruktion von Gussteilen.
• Erstellen von Fahr-, Stunden- und Raumplänen
• Lösung NP-schwerer Aufgaben (Problem des Handlungsreisenden, Rucksackproblem,...)
• Untersuchung des Fermatschen Satzes
• Technische Analyse im Finanzwesen

Praktisches Vorgehen

Der typische GA umfasst die folgenden Schritte:

1. Initialisierung: Erzeugen einer ausreichend großen Menge unterschiedlicher „Individuen“ (Lösungskandidaten). Diese bilden die erste Generation.
2. Evaluation: Für jeden Lösungskandidaten der aktuellen Generation wird anhand einer Zielfunktion (auch Fitness-Funktion genannt) ein Wert bestimmt, der seine Güte angibt.
3. Selektion: Zufällige Auswahl von Lösungskandidaten aus der aktuellen Generation. Dabei werden Lösungskandidaten mit besseren Zielfunktionswerten mit einer höheren Wahrscheinlichkeit ausgewählt.
4. Rekombination: die Daten (Genome) der ausgewählten Individuen werden gemischt und daraus neue Individuen erzeugt (Vermehrung)
5. Mutation: Zufällige Veränderung der neuen Individuen. (beachte: geeignete Diversifikation)
6. Aus den neuen Individuen und eventuell, je nach Gestaltung des Verfahrens, auch aus den Individuen der aktuellen Generation werden die Mitglieder der neuen Generation ausgewählt, die dann zur aktuellen wird.
7. Wenn ein Abbruchkriterium erfüllt ist, wird der beste gefundene Lösungskandidat als Ergebnis ausgegeben und der Algorithmus beendet. Sonst wird er mit Schritt 2 fortgesetzt.

Eine theoretische Untersuchung des Konvergenzverhaltens liefert der Schemasatz von John H. Holland.

Beispiele

„Festlegungen“ eines konkreten genetischen Algorithmus:

• Sei 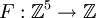$F:\mathbb{Z}^5 \to \mathbb{Z}$ eine Fitness-Funktion, die wie folgt definiert ist:

$\qquad \forall \; a,b,c,d,e \in \mathbb{Z} : \quad f(a,b,c,d,e) = |a-b| + |b-c |+ |c-d|+ |d-e| + |e-a|$

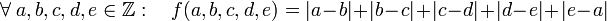
• Als Genom eines Individuums nehmen wir (hier) einfach die Variablen der Fitness-Funktion, also die Liste (a,b,c,d,e)
• Ziel ist es, die Fitness-Funktion f zu minimieren, also eine Eingabe zu finden, sodass die Funktion einen möglichst niedrigen Wert zurückliefert.
• Als Rekombination wählen wir ein einfaches Crossover mit 2 Eltern-Genomen, wobei die Eltern aus der alten Population zufällig gewählt werden:
  • Wir wählen (zufällig) eine Position $p \in \{ 0,1,2,3,4 \}$.
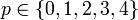  • Das Kind-Genom wird aus den beiden Eltern-Genomen zusammengesetzt, indem p viele vordere Allele des Genoms des einen Elternteils und 5 − p viele hintere Allele des Genoms des anderen Elternteils kopiert werden.
  • Sind beispielsweise die Eltern-Genome

G₀ = (18, − 3,5,9,8) und G₁ = (14,13,33,2,15) sowie p = 2, dann ist das Kind-Genom G_c = (18, − 3,33,2,15).

• Als Mutation wählen wir für jede Position

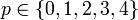$p \in \{ 0,1,2,3,4 \}$ im Genom eine einfache Addition an dieser Position um eine Zahl 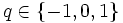$q \in \{ -1,0,1 \}$. Diese Mutation komme mit einer Wahrscheinlichkeit von 1% pro Generationswechsel und Position vor.

• Die Selektion sei wie folgt: Von der gemeinsamen Population von Eltern und Kindern werden die entsprechend der Fitness-Funktion besten ausgewählt, und zwar so viele, wie es Individuen in der ursprünglichen Eltern-Population gab.
• Startpopulation:
  • Sie bestehen aus 50 Individuen.
  • Jedes Individuum bekommt für jedes seiner Gene eine zufällige Zahl aus $\left[-50,50 \right] \cap \mathbb{Z}$ zugeordnet.
• Abbruchkriterium: Wir brechen das Berechnen der Generationenfolge ab, wenn sich über die letzten 10 Generationen der Durchschnitt der Fitness aller Individuen der jeweiligen Population nicht geändert hat.
• Ausgabe des genetischen Algorithmus ist das Genom eines besten Individuums in der letzten Population (die Population zu der Zeit, wann abgebrochen wurde).

Lässt man diesen genetischen Algorithmus laufen, so wird man nach etwa 70 Generationen ein Ergebnis (a,b,c,d,e) haben, für das gilt: a = b = c = d = e. Dieses Ergebnis ist in diesem konkreten Fall optimal. Man sieht, dass es viele gleichwertige Ergebnisse geben kann, so z. B. (4,4,4,4,4) oder ( − 21, − 21, − 21, − 21, − 21).

Mutation binärer Zahlen

Eine Mutation von binären Zahlen ist im Kontext eines genetischen Algorithmus eine spezielle Mutation, die für Genome ausgelegt ist, die selbst eine binäre Zahl sind.

Bevorzugung der niederwertigeren Bits Eine Variante von Mutation von binären Zahlen ist folgendes Verfahren:

• Man wähle eine Stelle i der binären Zahl Z₀, wobei die niederwertigen Stellen mit einer exponentiell höheren Wahrscheinlichkeit ausgewählt werden als die höherwertigen.
• Man invertiere das Bit an dieser Stelle der binären Zahl um: Z₁ = Z₀XOR2ⁱ.
• Die daraus neu entstehende Zahl ist das mutierte Genom.

Ein Beispiel zur Veranschaulichung - eine Mutation einer 8-Bit-Zahl:

11001100 - die Zahl vor der Mutation

11000100 - danach (eine Mutation an der 5. Stelle)

Dieses Verfahren funktioniert auch bei Gleitkommazahlen, wenn diese als Zahl ohne Exponenten-Information geschrieben wird (also 1100110000,00 statt $1{,}10011 \cdot 2^9$).

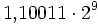Eine falsche Wahl der Mutationswahrscheinlichkeiten kann dazu führen, dass immer nur niederwertigen Stellen modifiziert werden, sodass die Mutationen letztendlich gar keinen nennenswerten Einfluss auf die Individuen oder den von ihnen abhängige Fitness-Funktions-Wert haben.

Vorteile

Genetische Algorithmen sind die schnellsten evolutionären Optimierungsverfahren, da die Individuen als diskrete Zahlenwerte in Binärform dargestellt werden und somit perfekt auf die aktuellen Rechnerplattformen zugeschnitten sind. Die gleichzeitige Verwendung mehrerer Individuen bietet zudem den Vorteil, hochgradig parallelisierbar zu sein.

Auch sind Genetische Algorithmen die einfachsten evolutionären Optimierungsverfahren, somit sind sie schnell zu implementieren und auf neue Probleme anzupassen.

Nachteile

Ein wichtiger Nachteil aller evolutionärer Optimierungsverfahren ist die Problematik, dass man nicht weiß, ob das erhaltene Ergebnis das Optimum der Fitnessfunktion darstellt. Es ist in der Praxis sehr schwer, geeignete Rekombinations- und Mutationsoperatoren zu finden, die für das Optimierungsproblem geeignet sind. Daher werden oft allgemeine Operatoren verwendet, welches zu einer längeren Laufzeit des Algorithmus führt.

Siehe auch

• Memetischer Algorithmus

Literatur

• David E. Goldberg, Genetic Algorithms in Search, Optimization, and Machine Learning, Addison-Wesley, 1989, ISBN 0-201-15767-5
• Ingo Rechenberg, Evolutionsstrategie '94, Frommann Holzboog, 1994, ISBN 3-7728-1642-8
• Poli, R., Langdon, W. B., McPhee, N. F. (2008), A Field Guide to Genetic Programming, freely available via Lulu.com.

Weblinks

• Einführung genetischer Algorithmen mit Anwendungsbeispiel, Steffen Harbich, 2007
• http://fog.neopages.org/tutorials.php Schritt für Schritt Anleitung für einen genetischen Algorithmus (auf Englisch)
• Wikiversity-Kurs Genetische Algorithmen.
• JGAP Freies Java Framework zur Implementierung genetischer Algorithmen, unterstützt auch die Genetische Programmierung; sehr viele Unit Tests zur Qualitätssicherung, umfangreiche Javadoc-Documentation
• HeuristicLab: Freies .NET Environment für heuristische Optimierung (genetische Algorithmen, Evolutionsstrategien, Nachbarschaftssuche, etc.)
• Informationen zum Thema Genetische Algorithmen
• Global Optimization Algorithms - Theory and Application