Eulersche Winkel

Eulersche Winkel oder auch Eulerwinkel sind eine Möglichkeit zur Beschreibung der Orientierung (Winkellage) von Objekten im dreidimensionalen Raum. Es handelt sich um drei Winkel, welche jeweils eine Drehung (Rotation) um bestimmte Achsen beschreiben und so eine Transformation zwischen zwei (kartesischen) Koordinatensystemen, dem Laborsystem und dem körperfesten System, definieren.

Definition

Eulersche Winkel in x-Konvention.
(Die Winkel α,β und γ entsprechen in den nebenstehenden Formeln den Größen Ψ,Θ und Φ)

Es existieren verschiedene Definitionen für die Eulerwinkel, die sich in der Wahl der Drehachsen unterscheiden. Von insgesamt 12 gleichwertigen möglichen Beschreibungen haben sich die unten angegebenen etabliert. Die angegebenen zugehörigen Drehmatrizen transformieren die Koordinaten des Körpers, der rotiert wird.

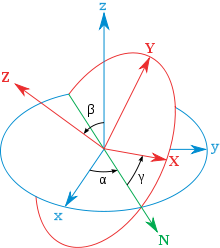
„x-Konvention“ (Z, X’, Z’’)

Zuerst wird um einen Winkel Ψ um die z-Achse des globalen Koordinatensystems (Z) gedreht. Es folgt eine Rotation um den Winkel Θ um die neue x-Achse (X') und schließlich um den Winkel Φ um die nach den beiden vorherigen Drehungen erhaltene z-Achse Z''.

$\begin{align} M_{zxz} & = \begin{pmatrix} \cos \Psi & - \sin \Psi & 0 \\ \sin \Psi & \cos \Psi & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 \\ 0 & \cos \Theta & - \sin \Theta \\ 0 & \sin \Theta & \cos \Theta \end{pmatrix} \begin{pmatrix} \cos \Phi & - \sin \Phi & 0 \\ \sin \Phi & \cos \Phi & 0 \\ 0 & 0 & 1 \end{pmatrix}\\ & = \begin{pmatrix} \cos \Psi \cos \Phi - \sin \Psi \cos \Theta \sin \Phi & - \cos \Psi \sin \Phi - \sin \Psi \cos \Theta \cos \Phi & \sin \Psi \sin \Theta \\ \sin \Psi \cos \Phi + \cos \Psi \cos \Theta \sin \Phi & \cos \Psi \cos \Theta \cos \Phi - \sin \Psi \sin \Phi & - \cos \Psi \sin \Theta \\ \sin \Theta \sin \Phi & \sin \Theta \cos \Phi & \cos \Theta \end{pmatrix} \end{align}$

„y-Konvention“ (Z, Y’, Z’’)

Zuerst wird um einen Winkel Ψ um die z-Achse des globalen Koordinatensystems (Z) gedreht. Es folgt eine Rotation um den Winkel Θ um die neue y-Achse (Y') und schließlich um den Winkel Φ um die nach den beiden vorherigen Drehungen erhaltene z-Achse Z''.

$\begin{align} M_{zyz} & = \begin{pmatrix} \cos \Psi & - \sin \Psi & 0 \\ \sin \Psi & \cos \Psi & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} \cos \Theta & 0 & \sin \Theta \\ 0 & 1 & 0 \\ - \sin \Theta & 0 & \cos \Theta \end{pmatrix} \begin{pmatrix} \cos \Phi & - \sin \Phi & 0 \\ \sin \Phi & \cos \Phi & 0 \\ 0 & 0 & 1 \end{pmatrix} \\ & = \begin{pmatrix} - \sin \Psi \sin \Phi + \cos \Psi \cos \Theta \cos \Phi & - \sin \Psi \cos \Phi - \cos \Psi \cos \Theta \sin \Phi & \cos \Psi \sin \Theta \\ \cos \Psi \sin \Phi + \sin \Psi \cos \Theta \cos \Phi & \cos \Psi \cos \Phi - \sin \Psi \cos \Theta \sin \Phi & \sin \Psi \sin \Theta \\ - \sin \Theta \cos \Phi & \sin \Theta \sin \Phi & \cos \Theta \end{pmatrix} \end{align}$

Da die resultierenden Matrizen Rotationsmatrizen sind, wird die Rücktransformation durch die Transponierte dargestellt. Z. B.:$M_{zyz}^{-1}=M_{zyz}^T$.

Luftfahrtnorm (DIN 9300) (Yaw-Pitch-Roll, Z, Y’, X’’)

→ Hauptartikel: Roll-Nick-Gier-Winkel

Lagewinkel-Drehung vom erdfesten Koordinatensystem (englisch world frame, Index g) ins körperfeste Koordinatensystem (englisch body frame, Index f)

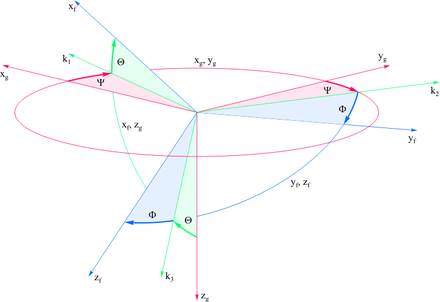
In der Luftfahrtnorm ist die Transformation des erdfesten bzw. „geodätischen“ Labor-Systems (englisch world frame, Index g) in das flugzeug- bzw. körperfeste System (englisch body frame, Index f) über die drei Lagewinkel Ψ, Θ und Φ definiert:

• Der Gierwinkel (englisch yaw angle) Ψ, auch Steuerkurs (englisch heading) oder Azimut (englisch azimuth angle) genannt, dreht in der x_g-y_g-Ebene um die z_g-Achse, wodurch die x_g-Achse in die Knotenachse k₁ und die y_g-Achse in die Knotenachse k₂ überführt wird. Hauptwertebereich: $- \pi < \Psi \le \pi$.

• Der Nickwinkel (englisch pitch angle) Θ, auch Längsneigung (englisch inclination angle) genannt, dreht in der x_f-z_g-Ebene um die (zuvor entstandene) k₂-Achse, wodurch die k₁-Achse in die x_f-Achse und die z_g-Achse in die Knotenachse k₃ überführt wird. Hauptwertebereich: $- \frac{\pi}{2} \le \Theta \le \frac{\pi}{2}$.

• Der Rollwinkel (englisch roll angle) Φ, auch Querneigung oder Hängewinkel (englisch bank angle) genannt, dreht in der y_f-z_f-Ebene um die (zuvor entstandene) x_f-Achse, wodurch die (in der ersten Teildrehung entstandene) k₂-Achse schließlich in die y_f-Achse und die (in der zweiten Teildrehung entstandene) k₃-Achse in die z_f-Achse überführt wird. Hauptwertebereich: $- \pi < \Phi \le \pi$.

Lagewinkel-Drehung vom erdfesten ins flugzeugfeste Koordinatensystem. Roll-Nick-Gier ZYX

Die Transformationsmatrix setzt sich dann aus den drei Einzeldrehmatrizen für die jeweiligen Winkel zusammen. Dabei ist die Drehreihenfolge von rechts nach links zu lesen; also in der Reihenfolge $\Psi \rightarrow \Theta \rightarrow \Phi$:

$\begin{align} M_{fg} & = \begin{pmatrix} 1 & 0 & 0 \\ 0 & \cos \Phi & \sin \Phi \\ 0 & - \sin \Phi & \cos \Phi \end{pmatrix} \begin{pmatrix} \cos \Theta & 0 & - \sin \Theta \\ 0 & 1 & 0 \\ \sin \Theta & 0 & \cos \Theta \end{pmatrix} \begin{pmatrix} \cos \Psi & \sin \Psi & 0 \\ - \sin \Psi & \cos \Psi & 0 \\ 0 & 0 & 1 \end{pmatrix} \\ & = \begin{pmatrix} \cos \Theta \cos \Psi & \cos \Theta \sin \Psi & - \sin \Theta \\ \sin \Phi \sin \Theta \cos \Psi - \cos \Phi \sin \Psi & \sin \Phi \sin \Theta \sin \Psi + \cos \Phi \cos \Psi & \sin \Phi \cos \Theta \\ \cos \Phi \sin \Theta \cos \Psi + \sin \Phi \sin \Psi & \cos \Phi \sin \Theta \sin \Psi - \sin \Phi \cos \Psi & \cos \Phi \cos \Theta \end{pmatrix} \end{align}$

Neben der hier gezeigten (ZY'X'')-Konvention sind weitere Varianten im Gebrauch, sehr häufig Roll-Pitch-Yaw (XY'Z''). Dabei ist lediglich die Reihenfolge der Rotationsmatrizen bei der Multiplikation zu ändern, um die gesamte Transformationsmatrix zu erhalten, bei Roll-Pitch-Yaw also M_fg = R_z(Ψ)R_y(Θ)R_x(Φ)

Beispiel

Der Gewichtsvektor hat beispielsweise im erdfesten Koordinatensystem nur eine z-Komponente (in Richtung Erdmittelpunkt):

$G_g = \begin{pmatrix} 0 \\ 0 \\ mg \end{pmatrix}$

Die Transformation ins flugzeugfeste Koordinatensystem geschieht dann durch Linksmultiplikation des erdfesten Gewichtsvektors G_g mit der Transformationsmatrix M_fg:

$\begin{align} G_f &= M_{fg}G_g \\ & = \begin{pmatrix} \cos \Theta \cos \Psi & \cos \Theta \sin \Psi & - \sin \Theta \\ \sin \Phi \sin \Theta \cos \Psi - \cos \Phi \sin \Psi & \sin \Phi \sin \Theta \sin \Psi + \cos \Phi \cos \Psi & \sin \Phi \cos \Theta \\ \cos \Phi \sin \Theta \cos \Psi + \sin \Phi \sin \Psi & \cos \Phi \sin \Theta \sin \Psi - \sin \Phi \cos \Psi & \cos \Phi \cos \Theta \end{pmatrix} \begin{pmatrix} 0 \\ 0 \\ mg \end{pmatrix} \\ & = \begin{pmatrix} \ldots & \ldots & - \sin \Theta \\ \ldots & \ldots & \sin \Phi \cos \Theta \\ \ldots & \ldots & \cos \Phi \cos \Theta \end{pmatrix} \begin{pmatrix} 0 \\ 0 \\ mg \end{pmatrix}\\ & = \begin{pmatrix} -\sin \Theta \\ \sin \Phi \cos \Theta \\ \cos \Phi \cos \Theta \end{pmatrix} mg \end{align}$

Physikalisch richtig wirkt das Gewicht also bei vorhandenem Nickwinkel Θ beispielsweise auch in die negative x_f-Richtung, also im Flugzeug nach hinten.

Herleitung im allgemeinen Fall

Für eine beliebige Wahl der Drehachsenreihenfolge kann die sich ergebende Drehmatrix durch die Zuhilfenahme des folgenden Zusammenhangs einfach hergeleitet werden:

Die Drehmatrizen um die globalen Achsen sind bekannt. Wenn nun um eine bereits verdrehte Achse erneut gedreht werden soll, dann entspricht das der Drehmatrix um die entsprechende globale Achse, allerdings in einer transformierten Vektorbasis. Die Transformationsmatrix (Basiswechselmatrix) ist dabei gerade die vorhergehende Drehung.

Seien A und B zwei Drehmatrizen um die beiden globalen Achsen G und H. Zur Berechnung der Drehmatrix zu der Reihenfolge $(G,H^\prime)$ beobachtet man, dass die Drehmatrix für die zweite Drehung um H der basistransformierten Matrix $\tilde B = A B A^{-1}$ entsprechen muss. Dadurch erhält man für die resultierende Gesamtdrehmatrix $C = \tilde B A = A B A^{-1} A = A B$. Für eine größere Anzahl von Drehungen erfolgt der Nachweis analog.

Durch diese Darstellung ergibt sich, dass sich die Drehmatrix für eine beliebige Drehreihenfolge in nacheinander verdrehten Achsen durch die einfache Multiplikation von Drehmatrizen um globale Koordinatenachsen ergibt – allerdings in umgekehrter Reihenfolge.

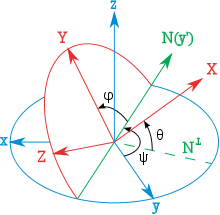
Ergebnis, Interpretation

Das erhaltene Koordinatensystem mit den Achsen X'', Y'' und Z'' ist das sogenannte körperfeste System. Die Winkel ϕ und θ geben dabei die Lage der Z''-Achse gegenüber dem körperfesten System an („Drehung“ und „Kippung“); der Winkel ψ beschreibt die Eigendrehung des Körpers um sie. Dem entsprechen folgende Namenskonventionen:

• Flugsteuerung (Rollwinkel, Nickwinkel, Gierwinkel)
• Kreiseltheorie: Präzession, Nutation und Spin oder Eigenrotation
• Azimut, Höhenwinkel oder Elevation und Rotation

Mathematische Eigenschaften

Die Abbildung, die den Euler-Winkeln die zugehörige Drehmatrix zuordnet, besitzt kritische Punkte, in denen diese Zuordnung nicht lokal umkehrbar ist und man von einem sogen. „Gimbal Lock“ spricht. Im Fall der og. x- oder y-Konvention tritt dieser stets dann auf, wenn der zweite Rotationswinkel gleich null wird und der Drehvektor der ersten Drehung damit derselbe ist wie der Drehvektor der zweiten Drehung. Das aber bedeutet, dass es für eine Rotation um die z-Achse beliebig viele Eulerwinkel mit α = Z + Z' gibt.

Bei der Definition der Lagewinkel nach der Luftfahrtnorm liegen die kritischen Punkte bei $\textstyle\Theta = \pm \frac{\pi}{2}$.

Nachteile, Alternativen

Zur Darstellung von Drehungen haben Eulerwinkel mehrere Nachteile:

• Die oben erwähnte Singularität führt dazu, dass eine einzige Drehung durch unterschiedliche Eulerdrehungen ausgedrückt werden kann. Dies führt zu einem Phänomen, das als Gimbal Lock bekannt ist.
• Die korrekte Kombination von Drehungen im Euler-System ist nicht intuitiv anzugeben, da sich die Drehachsen verändern.

Andere Möglichkeiten, die Orientierung zu beschreiben und teils diese Nachteile zu umgehen, sind Rotationsmatrizen oder Quaternionen.

Anwendungen

In der Theoretischen Physik werden die eulerschen Winkel zur Beschreibung des Starren Körpers benutzt. Eine praktische Anwendung ergibt die bekannte kardanische Aufhängung ^[1] der technischen Mechanik.

In der Kristallographie werden die eulerschen Winkel zur Beschreibung der Kreise des Röntgendiffraktometers und zur Beschreibung der Orientierungsdichteverteilungsfunktion von Texturen verwendet.

In der Astronomie sind die eulerschen Winkel unter anderen Bezeichnungen als Bahnelement eines Objekts geläufig.

In der Computergrafik werden die eulerschen Winkel zur Beschreibung der Orientierung eines Objektes verwendet.

In der Festkörper-NMR werden die eulerschen Winkel zur theoretischen Beschreibung und zur Simulation von Spektren benutzt.

Weblinks

 Commons: Euler angles – Album mit Bildern und/oder Videos und Audiodateien

 Wikibooks: Die Mechanik starrer Körper, Die eulerschen Winkel – Lern- und Lehrmaterialien

• Eric W. Weisstein: Euler Angles. In: MathWorld. (englisch)

Einzelnachweise

1. ↑ Der Zusammenhang zwischen den eulerschen Winkeln und der kardanischen Aufhängung ist u.a. in Kapitel 11.7 des folgenden Buches dargestellt: U. Krey, A. Owen: Basic Theoretical Physics - A Concise Overview. Springer-Verlag, Berlin 2007.