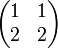Nullteilerfrei

In der abstrakten Algebra ist ein Nullteiler eines kommutativen Ringes R ein vom Nullelement 0 verschiedenes Element a, für das es ein vom Nullelement 0 verschiedenes Element b gibt, so dass ab = 0.

Definition

Ist R ein Ring und 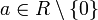$a \in R\setminus \{0\}$, dann unterscheidet man zwischen:

• Linksnullteiler: Es gibt ein Element 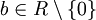$b \in R\setminus \{0\}$, so dass ab = 0.
• Rechtsnullteiler: Es gibt ein Element 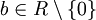$b \in R\setminus \{0\}$, so dass ba = 0.
• (zweiseitiger) Nullteiler: a ist sowohl Links- als auch Rechtsnullteiler.
• Linksnichtnullteiler: a ist kein Linksnullteiler.
• Rechtsnichtnullteiler: a ist kein Rechtsnullteiler.
• (zweiseitiger) Nichtnullteiler: a ist weder Links- noch Rechtsnullteiler.

In nichtkommutativen Ringen müssen Linksnullteiler keine Rechtsnullteiler sein und umgekehrt, bei kommutativen Ringen hingegen fallen alle sechs Begriffe schlicht zu Nullteiler und Nichtnullteiler zusammen.

Ist 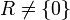$R \neq \{0\}$, dann ist 0 stets Nullteiler, und man nennt von 0 verschiedene Links-, Rechts- oder zweiseitige Nullteiler echt. Ein Ring ohne echte Links- und ohne echte Rechtsnullteiler heißt nullteilerfrei.

Ein nullteilerfreier, kommutativer Ring mit Einselement 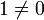$1 \neq 0$ heißt Integritätsring.

Beispiele

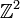Der Ring $\mathbb{Z}$ der ganzen Zahlen ist nullteilerfrei, der Ring $\mathbb{Z}^2$ (mit komponentenweiser Addition und Multiplikation) enthält die Nullteiler (0,1) und (1,0), denn $(0, 1) \cdot (1, 0) = (0, 0)$.

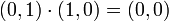Jeder Körper ist nullteilerfrei.

Der Restklassenring 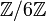$\mathbb{Z}/6\mathbb{Z}$ hat die Nullteiler 2, 3 und 4, denn $2 \cdot 3 \equiv 4 \cdot 3 \equiv 0 \mod 6$.

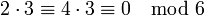Allgemein ist für eine natürliche Zahl n > 1 der Restklassenring 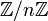$\mathbb{Z}/n\mathbb{Z}$ genau dann nullteilerfrei (sogar ein Körper), wenn n eine Primzahl ist.

Der Ring der reellen 2x2-Matrizen enthält den Nullteiler

$\begin{pmatrix} 1 & 1 \\ 2 & 2 \end{pmatrix}$

denn

$\begin{pmatrix} 1 & 1 \\ 2 & 2 \end{pmatrix} \cdot \begin{pmatrix} 1 & 1 \\ -1 & -1 \end{pmatrix} = \begin{pmatrix} 2 & -1 \\ 2 & -1 \end{pmatrix} \cdot \begin{pmatrix} 1 & 1 \\ 2 & 2 \end{pmatrix} = \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix}.$

Allgemein sind die Nullteiler im Ring der $n\times n$ Matrizen über einem Körper oder Integritätsring genau die Matrizen mit Determinante 0 (hier gibt es trotz fehlender Kommutativität keinen Unterschied zwischen Links- und Rechtsnullteilern).

Eigenschaften

In Ringen ist ein Element genau dann Links-, Rechts- oder zweiseitiger Nichtnullteiler, wenn es Links-, Rechts- bzw. zweiseitig kürzbar ist.

Idempotente Elemente ungleich 1 eines Rings sind Nullteiler, denn aus a² = a folgt 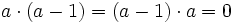$a \cdot (a - 1) = (a - 1) \cdot a = 0$. Nilpotente Elemente ungleich 0 (x mit xⁿ = 0 für ein $n \in \mathbb{N}$) sind trivialerweise Nullteiler.

Nullteiler sind keine Einheiten, denn wäre a invertierbar und ab = 0, dann wäre $0= a^{-1} \cdot 0 = a^{-1}ab = b$.

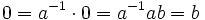In einem nichtkommutativen Ring mit Einselement (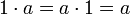$1 \cdot a = a \cdot 1 = a$ für alle a) gilt diese Aussage nur so: Ein Linksnullteiler hat kein Linksinverses. Jedoch kann ein Linksnullteiler ein Rechtsinverses haben. Analoges gilt für Rechtsnullteiler. (Ein beidseitiger Nullteiler hat demnach auch hier kein Inverses.)

Ist a ein Linksnullteiler, dann ist offensichtlich für jedes b das Produkt ba ebenfalls ein Linksnullteiler oder gleich null. Das Produkt ab muss aber kein Links- oder Rechtsnullteiler sein (siehe dazu das Beispiel des Matrixrings R im Artikel Einheit (Mathematik), dessen Elemente A und B einseitige Nullteiler sind, die jeweils einseitige Inverse voneinander sind, da AB = E die Einheitsmatrix ist).