Nilpotenz

Nilpotenz ist ein Begriff aus der Ringtheorie, einem Teilgebiet der Mathematik: Ein Element x eines Rings wird als nilpotent bezeichnet, wenn eine positive natürliche Zahl n existiert, so dass xⁿ = 0. Ein Ideal I von R wird als nilpotent bezeichnet, wenn eine positive natürliche Zahl n existiert, so dass Iⁿ = 0.

Beispiele

• Diese Definition lässt sich insbesondere auf quadratische Matrizen anwenden. Beispielsweise ist die Matrix

$A = \begin{pmatrix} 0&1&0\\ 0&0&1\\ 0&0&0\end{pmatrix}$

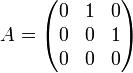
nilpotent, weil A³ = 0.

Für spezielle Eigenschaften nilpotenter Matrizen siehe den Artikel nilpotente Matrix.

• Im Restklassenring 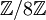$\mathbb{Z} / 8\mathbb{Z}$ sind die Restklassen von 0, 2, 4 und 6 nilpotent, da jeweils ihre dritte Potenz kongruent zu 0 modulo 8 ist. In diesem Ring ist jedes Element entweder nilpotent oder Einheit.

• Im Restklassenring 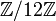$\mathbb{Z} / 12\mathbb{Z}$ sind die nilpotenten Elemente genau die Restklassen von 0 und 6.

• Das Nullelement eines Ringes ist stets nilpotent, da 0¹ = 0 ist.

Eigenschaften

Die Menge aller nilpotenten Elemente eines kommutativen Ringes bildet ein Ideal, das so genannte Nilradikal.

Der Durchschnitt aller Primideale in einem kommutativen Ring mit 1 ist genau das Nilradikal.

Sei im folgenden R ein Ring, a ein nilpotentes Element von R und n die kleinste natürliche Zahl mit aⁿ = 0.

• Ist 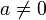$a \neq 0$, dann ist n > 1 und a ist Nullteiler, denn aa^{n − 1} = 0 und $a^{n-1} \neq 0$.

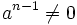Ist zusätzlich R ein Ring mit 1, dann gilt:

• a ist nicht invertierbar (bzgl. der Multiplikation), denn aus ab = 1 für ein Ringelement b folgt der Widerspruch 0 = aⁿb = a^{n − 1} (n war minimal gewählt!).
• 1-a ist invertierbar, denn es gilt (1 − a)(1 + a + a² + ... + a^{n − 1}) = 1 − aⁿ = 1 = (1 + a + a² + ... + a^{n − 1})(1 − a).
• Ist b eine Einheit von R, dann ist auch b + a invertierbar, was man durch Betrachtung der Darstellung als 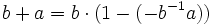$b+a = b\cdot (1-(-b^{-1}a))$ sieht.

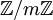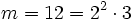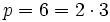Sei R ein Restklassenring $\mathbb{Z} / m\mathbb{Z}$ und p das Produkt aller Primteiler von m, d. h. aller Primzahlen die in der Primfaktorzerlegung (PFZ) von m auftreten. Z. B. für $m=12=2^2\cdot 3$ ist $p=6 = 2\cdot 3$. Dann sind die nilpotenten Elemente von R genau die Restklassen von ganzen Zahlen, die Vielfache von p sind. Die Beweisidee ist folgende: Ist k der größte Exponent, der in der PFZ vom m auftritt, dann ist p^k ein Vielfaches von m; jede Zahl, für die eine Potenz ein Vielfaches vom m ist, muss bereits selbst jeden Primteiler von m besitzen.