Kürzbarkeit — ist eine Eigenschaft von Elementen einer algebraischen Struktur. Inhaltsverzeichnis 1 Kürzbare/reguläre Elemente 1.1 Definition 1.2 Bemerkung 1.3 Beispiel … Deutsch Wikipedia
Halbgruppe — In der Mathematik ist eine Halbgruppe eine algebraische Struktur bestehend aus einer Menge mit einer inneren zweistelligen Verknüpfung, die dem Assoziativgesetz genügt (also ein assoziatives Magma). Sie ist eine Verallgemeinerung einer Gruppe.… … Deutsch Wikipedia
Regulär — hat in verschiedenen Bereichen der Mathematik verschiedene Bedeutungen: In der abstrakten Algebra heißt ein Element einer algebraischen Struktur mit einer zweistelligen Operation regulär, wenn es kürzbar ist. Eine Halbgruppe heißt regulär, wenn… … Deutsch Wikipedia
Ideal (Mathematik) — In der abstrakten Algebra ist ein Ideal eine Teilmenge einer algebraischen Struktur mit mindestens einer multiplikativen zweistelligen Operation, die abgeschlossen bezüglich Produkten mit Elementen aus der gesamten Struktur ist. Die Ideale… … Deutsch Wikipedia
Idealsystem — In der abstrakten Algebra ist ein Ideal eine Teilmenge einer algebraischen Struktur mit mindestens einer multiplikativen zweistelligen Operation, die abgeschlossen bezüglich Produkten mit Elementen aus der gesamten Struktur ist. Die Ideale… … Deutsch Wikipedia
Idealtheorie — In der abstrakten Algebra ist ein Ideal eine Teilmenge einer algebraischen Struktur mit mindestens einer multiplikativen zweistelligen Operation, die abgeschlossen bezüglich Produkten mit Elementen aus der gesamten Struktur ist. Die Ideale… … Deutsch Wikipedia
X-Ideal — In der abstrakten Algebra ist ein Ideal eine Teilmenge einer algebraischen Struktur mit mindestens einer multiplikativen zweistelligen Operation, die abgeschlossen bezüglich Produkten mit Elementen aus der gesamten Struktur ist. Die Ideale… … Deutsch Wikipedia
Idealoperator — In der abstrakten Algebra ist ein Ideal eine Teilmenge einer algebraischen Struktur mit mindestens einer multiplikativen zweistelligen Operation, die abgeschlossen bezüglich Produkten mit Elementen aus der gesamten Struktur ist. Die Ideale… … Deutsch Wikipedia
Injektivität — Eine injektive Funktion; X ist die Definitionsmenge und Y die Zielmenge. (Die Bildmenge besteht hier aus den Elementen A, B und D) Injektivität oder Linkseindeutigkeit ist eine Eigenschaft einer mathematischen Funktion bzw. Relation. Sie besagt,… … Deutsch Wikipedia
Nullteilerfrei — In der abstrakten Algebra ist ein Nullteiler eines kommutativen Ringes R ein vom Nullelement 0 verschiedenes Element a, für das es ein vom Nullelement 0 verschiedenes Element b gibt, so dass ab = 0. Definition Ist R ein Ring und , dann… … Deutsch Wikipedia
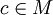 heißt linkskürzbar oder linksregulär, wenn für alle
heißt linkskürzbar oder linksregulär, wenn für alle 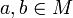 gilt:
gilt: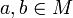 gilt:
gilt: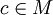 heißt zweiseitig kürzbar bzw. zweiseitig regulär oder einfach nur kürzbar bzw. regulär, wenn c links- und rechtskürzbar ist.
heißt zweiseitig kürzbar bzw. zweiseitig regulär oder einfach nur kürzbar bzw. regulär, wenn c links- und rechtskürzbar ist.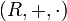 ist ein Element genau dann kürzbar, wenn es ein Nichtnullteiler ist.
ist ein Element genau dann kürzbar, wenn es ein Nichtnullteiler ist.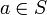 kürzbar ist.
kürzbar ist.
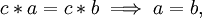
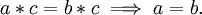
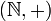 oder mit der üblichen Multiplikation
oder mit der üblichen Multiplikation 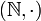 ist eine kürzbare Halbgruppe.
ist eine kürzbare Halbgruppe.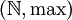 oder mit dem
oder mit dem 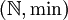 ist keine kürzbare Halbgruppe.
ist keine kürzbare Halbgruppe.