PageRank

Der PageRank-Algorithmus ist ein Verfahren, eine Menge verlinkter Dokumente, wie beispielsweise das World Wide Web, anhand ihrer Struktur zu bewerten bzw. zu gewichten. Dabei wird jedem Element ein Gewicht, der PageRank, aufgrund seiner Verlinkungsstruktur zugeordnet. Der Algorithmus wurde von Larry Page (daher der Name PageRank) und Sergei Brin an der Stanford University entwickelt und von dieser zum Patent angemeldet.^[1] Er diente der Suchmaschine Google des von Brin und Page gegründeten Unternehmens Google Inc. als Grundlage für die Bewertung von Seiten.

Der PageRank-Algorithmus ist eine spezielle Methode, die Linkpopularität einer Seite bzw. eines Dokumentes festzulegen. Das Grundprinzip lautet: Je mehr Links auf eine Seite verweisen, umso höher ist das Gewicht dieser Seite. Je höher das Gewicht der verweisenden Seiten ist, desto größer ist der Effekt. Das Ziel des Verfahrens ist es, die Links dem Gewicht entsprechend zu sortieren, um so eine Ergebnisreihenfolge bei einer Suchabfrage herzustellen, d.h. Links zu wichtigeren Seiten weiter vorne in der Ergebnisliste anzuzeigen.

Der PageRank-Algorithmus bildet einen zufällig durch das Netz surfenden Benutzer nach. Die Wahrscheinlichkeit, mit der dieser auf eine Webseite stößt, korreliert mit dem PageRank.

Der PageRank-Algorithmus

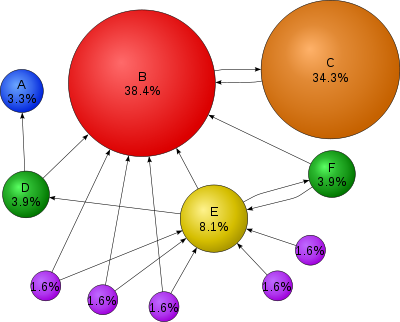Visualisierung des PageRank für einen einfachen Graphen mit Dämpfungsfaktor d = 0,85 nach dem Zufallssurfer-Modell. Die Größe der Kreise entspricht der jeweils angegebenen Wahrscheinlichkeit in Prozent, mit dem sich ein Surfer auf dieser Seite befindet. So wird Seite C nur von einer einzigen, aber sehr wichtigen Seite verlinkt und hat infolgedessen einen höheren PageRank als Seite E, obwohl diese von insgesamt sechs Seiten verlinkt wird. Da Seite A keine anderen Seiten referenziert, wurden bei der Berechnung des PageRanks Links zu allen vorhandenen Seiten hinzugefügt.

Das Prinzip des PageRank-Algorithmus ist, dass jede Seite ein Gewicht (PageRank) besitzt, das umso größer ist, je mehr Seiten (mit möglichst hohem eigenem Gewicht) auf diese Seite verweisen. Das Gewicht PR_i einer Seite i berechnet sich also aus den Gewichten PR_j der auf i verlinkenden Seiten j. Verlinkt j auf insgesamt C_j verschiedene Seiten, so wird das Gewicht von PR_j anteilig auf diese Seiten aufgeteilt. Folgende rekursive Formel kann als Definition des PageRank-Algorithmus angesehen werden:

$P\!R_i = \frac {1-d} {N} + d \, \sum_{\forall j \in \{(j,i)\}} {\frac {P\!R_j} {C_j}}$

Dabei ist N die Gesamtanzahl der Seiten und d ein Dämpfungsfaktor zwischen 0 und 1, mit dem ein kleiner Anteil des Gewichts (1 − d) einer jeden Seite abgezogen und gleichmäßig auf alle vom Algorithmus erfassten Seiten verteilt wird. Dies ist notwendig, damit das Gewicht nicht zu Seiten „abfließt“, die auf keine andere Seite verweisen. Oft wird die obige Formel auch ohne den Normierungsfaktor 1 / N angegeben.

Die Gleichung kann sowohl als Eigenvektorproblem der Matrix

$M_{\mathrm{EV} \,ij} = \frac {1-d} {N} + d \, T_{ij} \ ,$

$T_{ij} = \begin{cases} 1 / C_j, & \mbox{falls Seite }j\mbox{ zu Seite }i\mbox{ linkt} \\ 0, & \mbox{sonst} \end{cases}$

als auch (für d < 1) als Lösung des linearen Gleichungssystems

$M_{ij}\, P\!R_j = \frac {1-d} {N}$

mit

$M_{ij} = \delta_{ij} - d \, T_{ij}$

interpretiert werden, wobei δ_ij das Kronecker-Delta bezeichnet. Die Lösung des linearen Gleichungssystems

$P\!R_i = \frac {1-d} {N} \sum_j {M^{-1}}_{ij}$

kann analytisch oder numerisch erfolgen. Für d < 1 ist die Lösung des Gleichungssystems eindeutig. Durch Verwendung der Jacobi-Iteration zur numerischen Lösung ergibt sich obige rekursive Gleichung. Andere numerische Verfahren zur Matrixinvertierung, wie das Minimale-Residuum-Verfahren oder das Gauß-Seidel-Verfahren, konvergieren jedoch in der Regel schneller.

Der heute von Google verwendete Algorithmus hat vermutlich nicht mehr exakt diese Form, geht aber auf diese Formel zurück. Alternative Algorithmen sind das Verfahren der Hubs und Authorities von Jon Kleinberg, der Hilltop- und der TrustRank-Algorithmus.

Zufallssurfer-Modell

Normiert man den PageRank auf 1, so kann man das Gewicht einer Seite als Wahrscheinlichkeit interpretieren, dass ein zufälliger Surfer (siehe Zufallspfad) sich auf dieser Seite befindet. Ein zufälliger Surfer bewegt sich durch das Netz, indem er mit der Wahrscheinlichkeit d zufällig einen der ausgehenden Links der aktuellen Seite wählt. Mit Wahrscheinlichkeit 1 − d wählt er eine beliebige neue Seite. Hat eine Seite keine ausgehenden Links, können Links zu allen anderen vorhandenen Seiten hinzugefügt werden. Hierdurch wird erreicht, dass die Summe der PageRank-Werte aller Seiten gleich (und nicht kleiner) Eins ist.

Toolbar- und Verzeichnis-Werte

Informationen über den PageRank lassen sich aus der Google Toolbar und dem Google-Verzeichnis entnehmen. Der von Google in der Toolbar angezeigte PageRank liegt zwischen 0 und 10. Der im Google-Verzeichnis angegebene Wert lag bis Anfang 2008 zwischen 0 und 7, entspricht inzwischen aber dem in der Toolbar angezeigten Wert. Die angezeigten Werte bilden den realen PageRank auf einer logarithmischen Skala ab und geben das Ergebnis als gerundeten ganzzahligen Wert wieder.

Der in der Google-Toolbar angezeigte PageRank wurde früher alle dreißig Tage aktualisiert. Inzwischen wird das Intervall zwischen den Updates sehr unregelmäßig durchgeführt, die Intervalllänge schwankt dabei zwischen etwas weniger als dreißig bis zu über hundert Tagen.

Den höchsten PageRank von 10 erreichen nur sehr wenige Seiten, darunter google.com. Der deutsche Anbieter google.de hat nur einen Pagerank von acht, wikipedia.org von neun.

Manipulation

Aufgrund der wirtschaftlichen Bedeutung ist es inzwischen zu gezielten Manipulationen und Fälschungen gekommen. So wurde das System in der Praxis von Suchmaschinenoptimierern durch Spamming in Gästebüchern, Blogs und Foren, dem Betreiben von Linkfarmen und anderen unseriösen Methoden unterlaufen. Hierzu gehört unter anderem die Möglichkeit, den in der Toolbar angezeigten PageRank einer niedrig eingestuften Seite durch Weiterleitung auf eine bestehende Seite mit hohem PageRank zu spiegeln. Die Weiterleitung bewirkt ein Kopieren der Anzeige des hohen PageRanks der Zielseite mit dem folgenden Update. Wird die Weiterleitung anschließend entfernt, so wird dem Besucher für die Dauer des dann laufenden Intervalls der eigentlichen Seiteninhalt in Verbindung mit dem gespiegelten PageRank präsentiert. Der eigentliche PageRank-Wert und das Ranking im Suchalgorithmus ist hiervon unberührt, lediglich die Anzeige wird manipuliert. Dies kann beispielsweise in betrügerischer Absicht dafür genutzt werden, beim Verkauf der Domain oder von Links einen höheren Preis zu erzielen.

Anfang 2005 implementierte Google mit rel="nofollow" ein neues Attribut für Verweise, als Versuch, gegen Spam vorzugehen. Links, die mit diesem Attribut versehen werden, werden nicht für die PageRank-Berechnung berücksichtigt. Durch Kennzeichnung ausgehender Links kann so beispielsweise dem Gästebuch-, Blog- und Forum-Spamming entgegengewirkt werden. Allerdings ist diese Methode umstritten, da zum einen nicht alle Suchmaschinen das Attribut beachten und zum anderen die Links zwar nicht für die PageRank-Berechnung berücksichtigt werden, die verlinkten Seiten jedoch von den meisten Suchmaschinen weiterhin gecrawlt werden.

Geschichte

Die Idee des PageRank-Algorithmus stammt ursprünglich aus der Soziometrie und lässt sich in der Fachliteratur erstmalig 1953 bei Katz nachweisen. Bereits 1949 verwendete Seeley das Verfahren zur Erklärung des Zustandekommens des Status eines Individuums, allerdings gibt es in seiner Beschreibung noch keine Normierung auf die Anzahl der ausgehenden Kanten und keinen Dämpfungsterm. Letzterer wurde 1965 von Charles H. Hubbell eingeführt.

Kritik

Die Nachteile von PageRank im Überblick:

• Finanzkräftige Seitenbetreiber können sich Backlinks erkaufen und werden dadurch in Suchergebnissen höher positioniert. Dies führt dazu, dass statt qualitativ hochwertigem Inhalt oft die finanziellen Möglichkeiten über die Reihenfolge der Suchergebnisse entscheiden.
• Webmaster sehen oft im PageRank das einzige Bewertungskriterium für den Linktausch. Der Inhalt der verlinkten Seiten gerät in den Hintergrund.
• Der PageRank liefert keinen Beitrag zur qualitativen Messung von Websites.

Siehe auch

• Click Popularity
• Sponsorenlink
• Natural Listings

Einzelnachweise

1. ↑ Patent US6285999: Method for node ranking in a linked database. Angemeldet am 10. Januar 1997, Erfinder: Lawrence Page.

Literatur

• Amy N Langville und Carl D. Meyer: Google's pagerank and beyond: the science of search engine rankings, Princeton, N.J: Princeton University Press 2006. ISBN 978-1-4008-3032-9 (sample chapter)
• Arvind Arasu, Junghoo Cho, Hector Garcia-Molina, Andreas Paepcke und Sriram Raghavan: Searching the Web, Technical Report, Stanford University, USA, 2000 (online)
• Sergei Brin, Lawrence Page: The Anatomy of a Large-Scale Hypertextual Web Search Engine. In: Computer Networks and ISDN Systems 1998
• Charles H. Hubbell: An input-output approach to clique identification. In: Sociometry, Nummer 28, Seite 377-399, 1965
• Leo Katz: A new status index derived from sociometric analysis. In: Psychometrika, Nummer 18(1), Seite 39-43, 1953 [1]
• J. Seeley: The net of reciprocal influence: A problem in treating sociometric data, Canadian Journal of Psychology, 3, 234-240, 1949.

Weblinks

• eFactory: Erläuterungen und Berechnungsbeispiele zum PageRank-Verfahren
• Franz Embacher (Universität Wien): Bewertung von Webseiten durch Google
• Suchmaschinen-Doktor: Der PageRank-Algorithmus - Geschichte, Mathematik, Beispiele und Erweiterungen
• Links zum Thema PageRank im Open Directory Project