- Partitionsfunktion
-
Die Partitionsfunktionen geben die Anzahl der Möglichkeiten an, natürliche Zahlen in Summanden zu zerlegen. Üblicherweise betrachtet man die Zerlegungen ohne Berücksichtigung der Reihenfolge. Es gibt eine Reihe von Funktionen, bei denen an die Summanden zusätzliche Bedingungen gestellt werden, so z. B. dass jeder Summand nur einmal vorkommen darf.
Die Partitionsfunktion P(n), manchmal auch p(n) (Folge A000041 in OEIS) ist die einfachstmögliche Zerlegungsfunktion.
Inhaltsverzeichnis
Beispielwerte
Beispielwerte von p(n) und zugehörige Partitionen n p(n) Partitionen 0 1 (leere Summe) 1 1 (1) 2 2 (1+1), (2) 3 3 (1+1+1), (1+2), (3) 4 5 (1+1+1+1), (1+1+2), (2+2), (1+3), (4) 5 7 (1+1+1+1+1), (1+1+1+2), (1+2+2), (1+1+3), (2+3), (1+4), (5) 6 11 (1+1+1+1+1+1), (1+1+1+1+2), (1+1+2+2), (2+2+2), (1+1+1+3), (1+2+3), (3+3), (1+1+4), (2+4), (1+5), (6) Die Werte steigen danach schnell an (siehe Folge A000041 in OEIS):
- p(7) = 15
- p(8) = 22
- p(9) = 30
- p(10) = 42
- p(100) = 190.569.292
- p(200) = 3.972.999.029.388
- p(1000) = 24.061.467.864.032.622.473.692.149.727.991 ≈ 2,4 × 1031
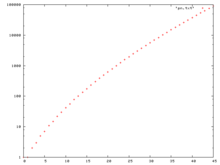
Asymptotisches Verhalten
Für große Werte von n gibt die Formel
einen guten Näherungswert für p(n). Insbesondere bedeutet dies, dass die Anzahl der Dezimalstellen von p(n) etwa proportional zur Quadratwurzel aus n ist: p(100) hat 9 Stellen (
 ), p(1000) hat 32 Stellen (
), p(1000) hat 32 Stellen ( ).
).p(4n) hat etwa doppelt so viele Stellen wie p(n).
p(k,n)
Dies ist eine Abwandlung der Partitionsfunktion, in der verlangt wird, dass der kleinste Summand größergleich k ist. Die "normale" Partitionsfunktion ist somit p(n) = p(1,n)
Beispielwerte
- p(1, 4) = 5
- p(2, 8) = 7
- p(3, 12) = 9
- p(4, 16) = 11
- p(5, 20) = 13
- p(6, 24) = 16
z. B.
-
Beispielwerte von p(k,n) p(k,n) k 1 2 3 4 5 6 7 8 9 10 n 1 1 2 2 1 3 3 1 1 4 5 2 1 1 5 7 2 1 1 1 6 11 4 2 1 1 1 7 15 4 2 1 1 1 1 8 22 7 3 2 1 1 1 1 9 30 8 4 2 1 1 1 1 1 10 42 12 5 3 2 1 1 1 1 1
Berechnung von p(n)
Eine erzeugende Funktion für p(n) ist:
Eine direkte Berechnung liefert die Formel
mit
und
die Hans Rademacher, aufbauend auf Erkenntnissen von Ramanujan und Godfrey Harold Hardy, fand.
Eine algebraische, geschlossene Form von p(n), die ohne unendliche Reihenentwicklung auskommt, wurde 2011 von Jan Hendrik Bruinier und Ken Ono veröffentlicht.[1][2] Genauer gesagt geben Bruinier und Ono eine Funktion P(n) an, so dass sich für jede natürliche Zahl n eine endliche Anzahl algebraischer Zahlen
 mit
mitfinden lassen. Darüber hinaus gilt, dass auch alle Werte P(αi) algebraisch sind.
Eigenschaften
wobei
 die Gaußklammer ist.
die Gaußklammer ist.Es gilt
- p(k,n) = 0, wenn k > n
- p(k,n) = 1, wenn k = n
- p(k,n) = p(k + 1,n) + p(k,n − k) sonst
Kongruenzen
Folgende Kongruenzen gehen auf Ramanujan zurück:
A. O. L. Atkin fand folgende Kongruenz:
Siehe auch
- Partition (Mengenlehre)
- Kombinatorik
- Pentagonalzahlensatz
- Der englische Begriff partition function wird in der Physik mit Zustandssumme übersetzt.
Weblinks
- http://mathworld.wolfram.com/PartitionFunctionP.html
- http://mathworld.wolfram.com/PartitionFunctionQ.html
Einzelnachweise
- ↑ J. H. Bruinier, K. Ono: An algebraic formula for the partition function, 2011.
- ↑ sueddeutsche.de: Eulers Erbe -- Mathematiker feiern Entdeckung in der Zahlentheorie , bezogen am 29. Januar 2011.
Wikimedia Foundation.




![A_k(n) = \!\!\!\!\sum_{0\le m < k \atop \operatorname{ggT} (m,k)=1}\!\!\!\!\exp \left\{
\frac{\pi i}{k} \left[ s(m,k) - 2 nm \right] \right\}.](6/9f6d5e4ce8b6d65a2ea98eff7e1721d9.png)




