- Zerlegung (Mathematik)
-
In der Mengenlehre ist eine Partition (auch Zerlegung oder Klasseneinteilung) einer Menge M eine Menge P, deren Elemente nichtleere, disjunkte Teilmengen von M sind, so dass jedes Element von M in genau einem Element von P enthalten ist.
Inhaltsverzeichnis
Beispiele
Die Mengenfamilie
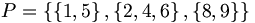 ist eine Partition der Menge
ist eine Partition der Menge 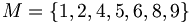 aber keine Partition von
aber keine Partition von 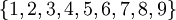 , da 3 und 7 nicht in den Teilmengen von P vorkommen.
, da 3 und 7 nicht in den Teilmengen von P vorkommen.Die Mengenfamilie
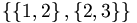 ist keine Partition von irgend einer Menge, da {1,2} und {2,3} beide die 2 enthalten, also nicht disjunkt sind.
ist keine Partition von irgend einer Menge, da {1,2} und {2,3} beide die 2 enthalten, also nicht disjunkt sind.Die Partitionen von {1, 2, 3} sind
Anzahl der Partitionen einer endlichen Menge
Die Anzahl der möglichen Partitionen einer n-elementigen Menge nennt man Bellsche Zahl Bn (nach Eric Temple Bell). Die ersten Bellzahlen sind
Partitionen und Äquivalenzrelationen
Ist eine Äquivalenzrelation ~ auf der Menge M gegeben, dann bildet die Menge der Äquivalenzklassen eine Partition von M, die meist als
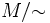 geschrieben wird.
geschrieben wird.Ist umgekehrt eine Partition P von M gegeben, dann können wir eine Äquivalenzrelation definieren durch:
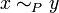 genau dann, wenn ein Element A in P existiert, in dem x und y enthalten sind. Als Formel lautet die Definition:
genau dann, wenn ein Element A in P existiert, in dem x und y enthalten sind. Als Formel lautet die Definition:Es ergibt sich die Gleichheit der Partitionen
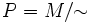 bzw. der Relationen
bzw. der Relationen 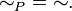 Damit sind Äquivalenzrelationen und Partitionen im Grunde gleichwertig.
Damit sind Äquivalenzrelationen und Partitionen im Grunde gleichwertig.Beispiel
Für eine feste natürliche Zahl m heißen ganze Zahlen x,y kongruent modulo m, wenn ihre Differenz x − y durch m teilbar ist. Kongruenz ist eine Äquivalenzrelation und wird mit
 bezeichnet. Die entsprechende Partition der Menge der ganzen Zahlen ist die Partition nach den Restklassen ganzer Zahlen modulo m, sie hat die Form
bezeichnet. Die entsprechende Partition der Menge der ganzen Zahlen ist die Partition nach den Restklassen ganzer Zahlen modulo m, sie hat die Formwobei
die einzelnen Restklassen bezeichnet, also die Untermengen der Zahlen gleichen Restes bezüglich m. (Man beachte, dass diese Notation für Restklassen nicht allgemein üblich ist, sie wurde nur gewählt, um die obige allgemeine Konstruktion zu illustrieren.)
Vergleich von Partitionen: Der "Partitionsverband"
Sind P und Q zwei Partitionen einer Menge M, dann nennen wir P feiner als Q, falls jedes Element von P Teilmenge eines Elements von Q ist. Anschaulich heißt das, dass jedes Element von Q selbst durch Elemente von P partitioniert wird.
Die Relation "feiner als" ist eine Halbordnung auf dem System aller Partitionen von X, und dieses System wird dadurch sogar zu einem Verband.
Siehe auch
Einzelnachweise
Wikimedia Foundation.

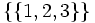
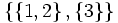
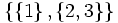
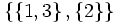
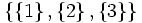

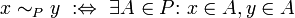
![\mathbb Z/{\equiv}=\{ [0]_\equiv , [1]_\equiv , \ldots , [m - 1]_\equiv \},](/pictures/dewiki/49/1bc673e5c8d9cf07bf266c079080d366.png)
![[k]_\equiv = \{\ldots,k-2m,k-m,k,k+m,k+2m,\ldots\}](/pictures/dewiki/48/0560b9bdcd59b302fb8ff6c0c440d826.png)