Auffälligkeit (Informationstheorie)

Die Auffälligkeit ist ein Maß für den Beitrag eines Zeichens an der Gesamtentropie eines Systems, das um 1965 von dem deutschen Kybernetiker Helmar Frank eingeführt wurde.

Definition

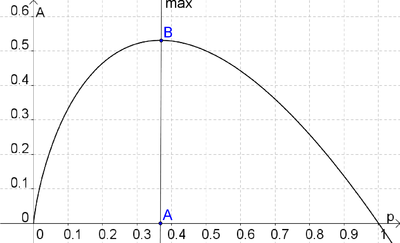
Die Funktion $A_z = - p_z \cdot \log_2{p_z}$

Bei der Untersuchung der von Shannon eingeführten Entropie konzentrierte sich Frank auf den Term, der den Beitrag einzelner Wahrscheinlichkeiten zur Gesamtentropie liefert. Dieser Beitrag ist das Produkt aus der Wahrscheinlichkeit p eines Ereignisses und seines Informationsgehaltes (Überraschungswertes) I(p) = − log ₂p:

$A_z = - p_z \cdot \log_2{p_z}$

Das Maximum dieser Funktion beträgt etwa $0{,}530\,737\,8$ bei:

$p_\mathrm{max} = \tfrac{1}{\mathrm e} \approx 0{,}367\,879\,44$.

(e - Eulersche Zahl)

Bei der Untersuchung zur Bedeutung dieser Funktion zog Frank, aufbauend auf den Arbeiten von Wilhelm Fucks, Parallelen zur menschlichen Wahrnehmung. Er definierte die Auffälligkeit eines Zeichens als seinen Beitrag zur Gesamtunsicherheit des Systems (Entropie)^[1].

Interpretation

$A_z = - p_z \cdot \log_2{p_z}$ mit Goldenem Schnitt

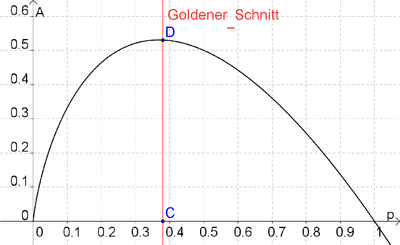
Frank und andere Wissenschaftler ^{[2] [3]} zogen Parallelen zwischen den Verhältnissen, die sich durch das Maximum der Auffälligkeit und den Goldenen Schnitt ergeben:

Maximum der Auffälligkeit:

$V_m = \frac{1 - \frac{1}{e}}{\frac{1}{ \mathrm e}} = \mathrm e - 1 \approx 1{,}71828$

Goldener Schnitt:

$\Phi = \frac{1 + \sqrt{5}}{2} \approx 1{,}618034$

Daraus schlossen sie, das die Auffälligkeit eine informationstheoretische Erklärung für einen Aspekt des ästhetischen Empfindens ist.

Einzelnachweise

1. ↑ Helmar G. Frank, Brigitte S. Meder: Einführung in die kybernetische Pädagogik, DTV Deutscher Taschenbuch, 1984, ISBN 3423041080
2. ↑ Horst Völz: Computer und Kunst, Reihe akzent 87. 2. Aufl. Urania-Verlag Leipzig Jena - Berlin 1990 (ab Seite 14 der PDF-Version) ISBN 3332002201
3. ↑ André Frank Zimpel: Der zählende Mensch. Was Emotionen mit Mathematik zu tun haben, Vandenhoeck & Ruprecht, 2008, ISBN 3525315422

Literatur

• Helmar G. Frank, Herbert W. Franke: Ästhetische Information. Estetika informacio. Eine Einführung in die kybernetische Ästhetik, Kopäd Verlag, 2002, ISBN 3929061821