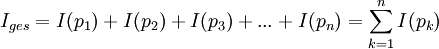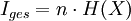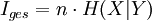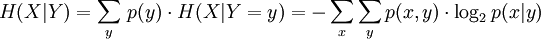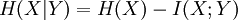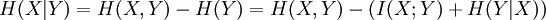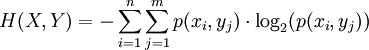Überraschungswert

Der Begriff der Information, wie er in der Informationstheorie nach Shannon^[1] verwendet wird, ist streng von dem gewöhnlichen Gebrauch dieses Begriffes zu unterscheiden. Insbesondere darf darin die Information nicht mit dem Begriff der Bedeutung gleichgesetzt werden. In Shannons Theorie können z. B. zwei Nachrichten, von denen eine von besonderer Bedeutung ist, während die andere nur "Unsinn" darstellt, genau die gleiche Menge an Information enthalten. Für den einfachen Fall, in dem nur zwischen zwei möglichen Nachrichten zu wählen ist, wird dabei willkürlich festgelegt, dass die Information, die mit dieser Situation verbunden ist, gleich 1 ist. Die beiden Nachrichten, zwischen denen bei einer solchen Auswahl entschieden werden soll, können dabei völlig beliebig sein. Eine Nachricht könnte z. B. der Text der Bibel sein und die andere Nachricht der einzelne Buchstabe "A". Diese beiden Nachrichten könnten dann beispielsweise durch die Symbole 0 und 1 codiert werden.

Allgemeiner wird durch eine beliebige Nachrichtenquelle eine Folge von Auswahlvorgängen aus einer Menge von elementaren Zeichen vorgenommen, wobei diese ausgewählte Folge dann die eigentliche Nachricht darstellt. Hierbei ist leicht einzusehen, dass die Wahrscheinlichkeiten der Zeichen bei der Erzeugung der Nachricht von besonderer Wichtigkeit sind. Denn wenn die aufeinanderfolgenden Zeichen ausgewählt werden, ist diese Auswahl, zumindest vom Standpunkt des Kommunikationssystems aus, von dieser Wahrscheinlichkeit bestimmt. Diese Wahrscheinlichkeiten sind in den meisten Fällen sogar voneinander abhängig, d. h. sie hängen von den vorangegangenen Auswahlereignissen ab. Ist z. B. das letzte Wort einer Wortfolge der Artikel "die", dann ist die Wahrscheinlichkeit dafür, dass als nächstes Wort wieder ein Artikel oder ein Verb auftritt, sehr gering.

Ein Maß, welches in besonderer Weise den natürlichen Anforderungen genügt, die man an dieses Informationsmaß stellt, entspricht genau dem, welches in der statistischen Physik als Entropie bekannt geworden ist. Wie dieses Informationsmaß von den entsprechenden Wahrscheinlichkeiten abhängt, wird im folgenden Abschnitt erklärt.

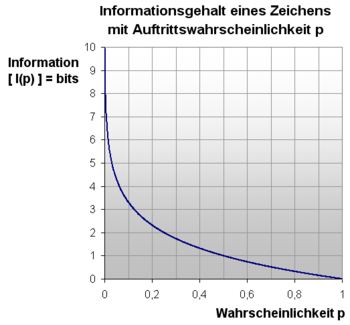
Der Informationsgehalt (oder auch Überraschungswert) einer Nachricht ist eine logarithmische Größe, die angibt, wie viel Information in dieser Nachricht übertragen wurde. Dieser Begriff wurde von Claude Shannon erstmals in seiner Informationstheorie formalisiert: Der Informationsgehalt eines Zeichens ist seine statistische Signifikanz. Er bezeichnet also die minimale Anzahl von Bits, die benötigt werden, um ein Zeichen (also eine Information) darzustellen oder zu übertragen. Wichtig ist dabei, dass dies nicht unbedingt der Anzahl der tatsächlich empfangenen Bits (der Datenmenge) entspricht, da der Informationsgehalt vom semantischen Kontext abhängig ist. Daher wird der Informationsgehalt mit einer anderen Einheit, dem Shannon (sh), gemessen.

Formal werden die zu übertragenden Informationen als Zeichen bezeichnet. Dabei steht nur ein endlicher Zeichenvorrat zur Verfügung, Zeichen können aber beliebig kombiniert werden. Die minimale Anzahl von Bits, die für die Darstellung oder Übertragung eines Zeichens benötigt werden, hängt nun von der Wahrscheinlichkeit ab, mit der ein Zeichen auftritt: für Zeichen, die häufig auftreten, verwendet man weniger Bits als für Zeichen, die selten verwendet werden. Datenkompressionstechniken machen sich das zu Nutze, insbesondere die Entropiekodierung, die Arithmetische Kodierung und die Huffman-Kodierung. Ein ähnliches Verfahren wird zum Ausbalancieren von Binärbäumen verwendet.

Je kleiner die Auftretenswahrscheinlichkeit eines Zeichens ist, desto höher ist sein Informationsgehalt. Andersrum ist der Informationsgehalt eines Zeichens sehr gering, wenn es sehr oft vorkommt.

Falls beide (alle) Zeichen gleich oft vorkommen, wird der mögliche Informationsgehalt eines Zeichens minimal.

Der Informationsgehalt eines Zeichens ist definiert durch $I(p(x)) = \log_a (\textstyle \frac{1}{p(x)}) = -\log_a( p(x))$.
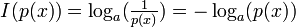a entspricht dabei der Anzahl der möglichen Zustände einer Nachrichtenquelle.

Im folgenden Text sei a=2, wodurch das Ergebnis in Bit geliefert wird. Analog zur Basis 2 lässt sich a für alle anderen Werte berechnen.

Die Anzahl der benötigten Bits (der Informationsgehalt I in Shannon) die mindestens nötig ist, um ein einzelnes Zeichen x mit der Auftretenswahrscheinlichkeit p = p(x) zu kodieren, berechnet sich folgend:

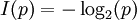$I(p) = -\log_{2}({p}) \,$   mit   $\,[I] = \mathrm{bit}$

Grundsätzlich wird der Informationsgehalt für statistisch unabhängige (unvorhersehbare/zufällige) Ereignisse und statistisch abhängige (vorhersehbare/gebundene/kontext-abhängige) Ereignisse unterschiedlich berechnet.

Informationsgehalt statistisch unabhängiger Ereignisse

Sei x₁x₂...x_n eine Folge von n statistisch unabhängig aufeinanderfolgenden Ereignissen. Der Informationsgehalt I_ges berechnet sich dann aus der Summe der Informationsgehalte jedes einzelnen Zeichens x_i mit der Auftretenswahrscheinlichkeit p_i = p(x_i).

$I_{ges} = I(p_1) + I(p_2) + I(p_3) + ... + I(p_n) = \sum_{k=1}^{n}{I(p_k)}$

Ebenso lässt sich der Informationsgehalt mit der Entropie H(X) (mittlerer Informationsgehalt eines Zeichens) berechnen.

$I_{ges} = n\cdot H(X)$

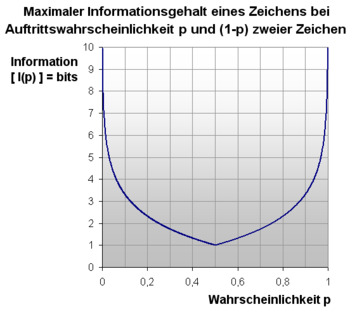
Bei einer Gleichverteilung der Wahrscheinlichkeiten p=p(x_i)=p(x_i+1) für alle Zeichen x_i aus dem Alphabet Z lässt sich die Gesamtinformation auch über die maximale Entropie bzw. die Alphabetsgröße |Z| berechnen:

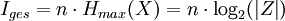$I_{ges} = n\cdot H_{max}(X)= n\cdot \log_{2}({|Z|})$  bzw.  $n\cdot I(p)$

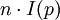
Bei der Gleichverteilung gilt immer: $p=\textstyle \frac{1}{|Z|}$

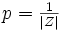
Der Informationsgehalt der beiden Quellen „01010101...“ und „10010110...“ ist aus der Betrachtung von statistisch unabhängigen Ereignissen nach obiger Formel gleich. Zu erkennen ist, dass die Zeichen der ersten Quelle durch eine sich wiederholende Struktur geordnet sind. Deshalb würde man intuitiv in der ersten Kette weniger Information als in der zweiten Kette vermuten. Bei der Betrachtung als statistisch unabhängiges Ereignis wird aber jedes Zeichen einzeln betrachtet und nicht der eventuelle Zusammenhang mehrerer Zeichen berücksichtigt.

Eine andere Definition der Information eines Zeichens liefert die bedingte Entropie. Bei ihr wird das Auftreten vorangegangener Zeichen berücksichtigt. Die aufeinanderfolgenden Zeichen werden in diesem Fall als statistisch abhängige Ereignisse betrachtet.

Informationsgehalt statistisch abhängiger Ereignisse

Bei statistisch abhängigen Ereignissen kennt man den Kontext der Ereignisse genauer und kann daraus Schlussfolgerungen ziehen, die den Informationsgehalt beeinflussen. Dabei können meistens die folgenden Ereignisse durch Ausschlussverfahren und Bindungen ‚erraten‘ werden. Ein Beispiel für statistisch abhängige Ereignisse ist ein Text in der deutschen Sprache: das 'c' tritt meistens paarweise mit einem 'h' oder 'k' auf. Andere Buchstaben unterliegen ebenfalls solchen paarweisen Bindungen.

Hierzu wird ähnlich wie bei statistisch unabhängigen Ereignissen der durchschnittliche und kontextsensitive Informationsgehalt eines Zeichens mit der Anzahl der vorhandenen Zeichen multipliziert:

$I_{ges} = n\cdot H(X|Y)$

Die bedingte Entropie berechnet sich folgend:

$H(X|Y)=\sum_{y}{\,}{p(y) \cdot H(X|Y = y )} = -\sum_{x}^{}\sum_{y}^{} p(x,y) \cdot \log_{2}{p(x|y)}$

Bedingte Entropie als Differenz von Quell-Information und Transinformation:

$H(X|Y) = H(X) - I(X;Y) \,$  

Interpretation: Seien X und Y zwei stationär abhängige Quellen. H(X) sei die stationär betrachtete Quell-Entropie. I(X; Y) ist die Transinformation, die Information die von X nach Y fließt, also die Menge an Information von der man von X auf Y schließen kann. Ist diese Information hoch, so ist auch die Abhängigkeit von X und Y hoch. Dementsprechend ist die über X nach einer Beobachtung Y nicht so hoch, da man nicht sehr viel neue Information über Y erhält.

Bedingte Entropie als Gesamtinformation abzüglich der Entropie von H(Y):

$H(X|Y) = H(X,Y) - H(Y) = H(X,Y) - ( I(X;Y) + H(Y|X) ) \,$  

Interpretation: Im statistisch abhängigen Fall zieht man von der Gesamtinformation (Verbundentropie) die gemeinsame Information (= I(X;Y)) von X und Y ab. Außerdem soll auch die neue Information, die Y mit sich bringt nicht mit eingerechnet werden, denn man möchte am Ende nur die Menge an Information von X herausbekommen, die X alleine beinhaltet. Deshalb rechnet man: H(X|Y) = H(X,Y) - I(X;Y) - H(Y|X)

Bemerkung: Die Information von statistisch abhängigen Ereignissen ist immer kleiner gleich der von statistisch unabhängigen Ereignissen, da wie folgt gilt: H(X|Y) ≤ H(X)

Verbundwahrscheinlichkeit H(X,Y)

Gibt es n mögliche Ereignisse x und m mögliche Ereignisse y, so ist die Verbundwahrscheinlichkeit p(y_j,x_i) die Wahrscheinlichkeit dafür, dass je ein Ereignis x_i paarweise mit einem Ereignis y_j auftritt.

Die Wahrscheinlichkeit, dass das Ereignis x_i paarweise mit dem Ereignis y_j auftritt ist $p(x_i) = \sum_{j=1}^{m}{p(x_i, y_j)}$.

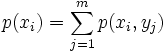Mit der bedingten Wahrscheinlichkeit ergibt sich die Verbundwahrscheinlichkeit dann zu $p(x_i, y_j) = p(x_i) \cdot p(y_j | x_i) = p(y_j) \cdot p(x_i | y_j) \,$.

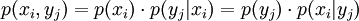Der mittlere Informationsgehalt der Verbundentropie je Ereignispaar statistisch abhängiger Ereignisse ist somit definiert durch:

$H(X,Y) = -\sum_{i=1}^{n} \sum_{j=1}^{m}{p(x_i,y_j)} \cdot \log_2( p(x_i,y_j))$

Bemerkungen

Informationsgehalt analoger Signale

Der Informationsgehalt analoger Signale kann berechnet werden, indem die zeitkontinuierlichen Signale mit einem A/D-Wandler in diskrete Werte überführt werden. Dann gilt der gleiche Formalismus, wie oben angegeben.

Die entscheidenden Kenngrößen sind hier die Bandbreite und das Signal-Rausch-Verhältnis. Dies ist vor allem dann relevant, wenn man sich wie in der Nachrichtentechnik dafür interessiert, Information über ein analoges Signal zu transportieren, da ja ein Signal keinesfalls mehr Information transportieren kann als es enthält.

Beispiele für statistisch unabhängige Ereignisse

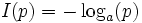$I(p) = -\log_{a}({p}) \,$  für  a = 2

In den folgenden Beispielen sei die Basis vom Logarithmus 2. Somit erhält man als Ergebnis die Einheit Bit

Beispiel 1

An einer Quelle tritt ein Zeichen x mit der Wahrscheinlichkeit p(x)=0,0625 auf. Für die maximale Effizienz zur Übertragung in einem Kanal ist eine Information von I(p(x)) = I(0,0625) = 4 bit für jedes Zeichen x notwendig sind.

Beispiel 2

Gegeben sei eine Zeichenkette „Mississippi“. Sie besteht aus n = 11 Zeichen.

Alphabet Z = {i,M,p,s} mit den Auftretenswahrscheinlichkeiten p(i)= 4/11; p(M)=1/11; p(p)=2/11; p(s)=4/11

Gesamtinformation: $I_{ges} = \sum_{i=1}^{n} I({p(z_i)}) = \sum_{i=1}^{11} I({p(z_i)})$

$\, = 4\cdot I(p(i)) + 1 \cdot I(p(M)) + 2 \cdot I(p(p)) + 4 \cdot I(p(s))\,$

$= 4\cdot 1,46\,\mathrm{bit} + 1\cdot 3,46\,\mathrm{bit} + 2\cdot 2,46\,\mathrm{bit} + 4\cdot 1,46\,\mathrm{bit}$

$= 5,84 \,\mathrm{bit} + 3,46 \,\mathrm{bit} + 4,92\,\mathrm{bit} + 5,84\,\mathrm{bit} = 20,05\,\mathrm{bit}$

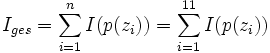
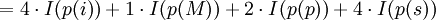
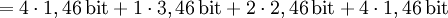
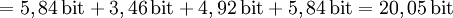
Daraus folgt die Gesamtbitanzahl von 21 bit, die notwendig ist, um das Wort „Mississippi“ binär optimal zu kodieren.

Beispiel 3

Alphabet Z = {a, b}  mit  p(a) = 0,01 und  p(b) = 0,99. Die Zeichenkette bestehe aus 100 Zeichen.

I(p(a)) = 6,64 bit (seltenes Auftreten ⇒ hohe Information im Falle des Auftretens)

I(p(b)) = 0,01 bit (häufiges Auftreten ⇒ wenig Information im Falles des Auftretens)

Gesamtinformation: I_ges = 1⋅I(p(a)) + 99⋅I(p(b)) = 8,07 bit

Damit folgt eine Gesamtinformation von 9 bit.

Man könnte auch sagen, dass der Informationsgehalt eines Zeichens umgekehrt proportional zum Logarithmus der Wahrscheinlichkeit ist, mit der man es erraten kann (der Entropie). Der Informationsgehalt ist also ein Maß für die maximale Effizienz, mit der eine Information übertragen werden kann.

Ein alternatives Maß für den Informationsgehalt einer Zeichenkette ist die Kolmogorov-Komplexität bzw. der algorithmische Informationsgehalt: er ist definiert als die Länge des kürzesten Programmes, das diese Zeichenkette erzeugen kann. Ein weiterer Ansatz ist die so genannte Algorithmische Tiefe, die besagt, wie aufwändig es ist, eine bestimmte Nachricht zu erzeugen. Gregory Chaitin ist ebenfalls über die Shannonsche Definition der Entropie einer Information hinausgegangen (siehe Algorithmische Informationstheorie).

In diesem Zusammenhang spielen auch die Kreuzentropie sowie die Kullback-Leibler-Divergenz als Maße für die durch eine schlechte Kodierung ausgelösten Verschwendungen von Bits eine Rolle.

Originalarbeiten und Belege

1. ↑ C. E. Shannon, Bell Syst. Techn. J. 30 (1951) 50

Siehe auch

Entropie, Blockentropie, Entropieschätzung, Datenmenge, Negentropie, Bedeutsamkeit, Informationsqualität, Algorithmische Informationstheorie, Kolmogorov-Komplexität, Überraschung, Auffälligkeit