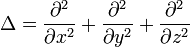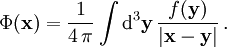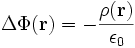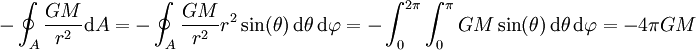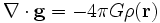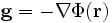Poisson Gleichung

Die Poisson-Gleichung (nach Siméon Denis Poisson) beschreibt ein Randwertproblem, bei welchem die Ableitungen eines Vektorfeldes auf der Oberfläche eines Volumens gegeben sind. Anwendung findet diese beispielsweise in der Elektrostatik (Gaußsches Gesetz). Ebenso kann man das Gravitationspotential einer gegebenen Massenverteilung bestimmen.

Mathematische Formulierung

Die Poisson-Gleichung lautet allgemein:

$\left(\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}+\frac{\partial^2}{\partial z^2}\right)\,\Phi(x,y,z) = -f(x,y,z)\,.$

Bei Angabe der Funktionswerte oder der Normalenableitung der Funktion Φ auf dem Rand des Gebietes ist die Lösung eindeutig und hängt stetig von den Randwerten und von f ab.

Der Differentialoperator in der Poisson-Gleichung

$\Delta =\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}+\frac{\partial^2}{\partial z^2}$

ist der Laplace-Operator. Die homogene Poisson-Gleichung, $\Delta \Phi = 0\,,$ heißt Laplace-Gleichung.

Der Poisson-Gleichung genügen beispielsweise das elektrostatische Potential und das Gravitationspotential. Dabei ist f proportional zur elektrischen Ladungsdichte beziehungsweise zur Massendichte.

Für eine räumlich beschränkte Ladungsdichte f ist die Lösung der Poisson-Gleichung Φ, die für große Abstände gegen Null geht, das Integral

$\Phi(\mathbf x)=\frac 1 {4\,\pi} \int \mathrm d^3 \mathbf y \, \frac{f(\mathbf y)}{|\mathbf x - \mathbf y |}\,.$

Jede Ladung 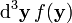$\mathrm d^3 \mathbf y \,f(\mathbf y)$ am Ort 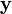$\mathbf y$ im kleinen Gebiet der Größe 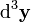$\mathrm d^3 \mathbf y$ trägt additiv zum Potential am Ort 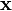$\mathbf x$ mit ihrem Coulomb-Potential (oder Kepler-Potential) 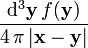$\frac{\mathrm d^3 \mathbf y\,f(\mathbf y)}{4\,\pi\,|\mathbf x - \mathbf y |}$ bei.

Anwendungen in der Physik

Elektrostatik

Da das elektrische Feld ein konservatives Feld ist, kann es über den Gradienten eines Potentials 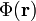$\Phi(\mathbf r)$ ausgedrückt werden, mit

$\mathbf E(\mathbf r)=-\nabla \Phi(\mathbf r)$.

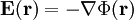Mit Anwendung eines weiteren Nabla-Operators ergibt sich

$\nabla \mathbf E(\mathbf r)= -\Delta \Phi(\mathbf r)$.

Gemäß der ersten Maxwellgleichung gilt jedoch auch

$\nabla \mathbf E(\mathbf r)=\frac{\rho(\mathbf r)}{\epsilon_0}$,

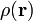wobei $\rho(\mathbf r)$ die Ladungsdichte und ε₀ die Permittivität sind.

Damit folgt für die Poisson-Gleichung des elektrischen Feldes

$\Delta \Phi(\mathbf r)=-\frac{\rho(\mathbf r)}{\epsilon_0}$

Gravitation

Die Gravitationsbeschleunigung ergibt sich aus dem Gravitationsgesetz zu

$\mathbf g=-\frac{GM}{r^2}\frac{\mathbf r}{r}$.

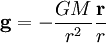Der Fluss durch die Oberfläche eines beliebigen Volumens ist dann

$\oint_A \mathbf g \, \mathrm d \mathbf A = -\oint_A \frac{GM}{r^2}\frac{\mathbf r}{r} \, \mathbf n \, \mathrm d A = -\oint_A \frac{GM}{r^2}\frac{\mathbf r}{r} \frac{\mathbf r}{r} \mathrm d A = -\oint_A \frac{GM}{r^2} \mathrm d A$,

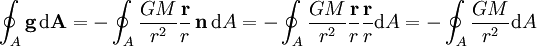wobei 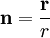$\mathbf n=\frac{\mathbf r}{r}$ der Normalenvektor ist. In Kugelkoordinaten gilt

$dA=r^2 \sin(\theta) \, \mathrm d\theta \, \mathrm d \varphi$,

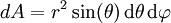woraus folgt

$-\oint_A \frac{GM}{r^2} \mathrm d A = -\oint_A \frac{GM}{r^2} r^2 \sin(\theta)\, \mathrm d\theta \, \mathrm d \varphi=-\int_0^{2\pi}\int_0^{\pi} GM \sin(\theta)\, \mathrm d\theta \, \mathrm d \varphi= -4 \pi G M$

Aus einer durch eine Massendichte 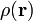$\rho(\mathbf r)$ beschriebene Massenverteilung ergibt sich die Gesamtmasse zu

$M=\int_V \rho(\mathbf r) \mathrm d V$.

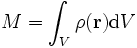Damit folgt

$-4 \pi G M = -4 \pi G \int_V \rho(\mathbf r) \mathrm d V$.

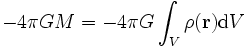Mit dem Satz von Gauß ergibt sich für das Integral jedoch auch

$\oint_A \mathbf g \, \mathrm d \mathbf A=\int_V \nabla \cdot \mathbf g\, \mathrm d V$,

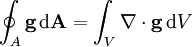und somit

$\int_V \nabla \cdot \mathbf g\, \mathrm d V = -4 \pi G \int_V \rho(\mathbf r) \mathrm d V$.

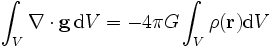Da die Form des Volumens beliebig ist, müssen die Integranden gleich sein, sodass

$\nabla \cdot \mathbf g = -4 \pi G \rho(\mathbf r)$

ist. Die Gravitation stellt ein konservatives Kraftfeld dar, sodass die Beziehung

$\mathbf g = -\nabla \Phi(\mathbf r)$

gilt. Damit ergibt sich die Poisson-Gleichung der Gravitation zu

$\nabla (\nabla \Phi(\mathbf r)) = \Delta \Phi(\mathbf r)= 4 \pi G \rho(\mathbf r)$,

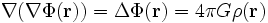wobei sich das Minuszeichen weghebt.

Quellen

• Richard Courant und David Hilbert, Methoden der mathematischen Physik, Band 1, Springer Verlag, 1968 (zuerst 1924)

Weblinks

Norbert Dragon, Stichworte und Ergänzungen zu Rechenmethoden der Physik