- Poisson-Verteilung
-
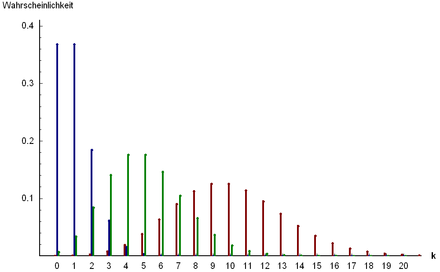
Die Poisson-Verteilung (benannt nach dem Mathematiker Siméon Denis Poisson) ist eine diskrete Wahrscheinlichkeitsverteilung, die beim mehrmaligen Durchführen eines Bernoulli-Experiments entsteht. Letzteres ist ein Zufallsexperiment, das nur zwei mögliche Ergebnisse besitzt (z. B. „Erfolg“ und „Misserfolg“). Führt man ein solches Experiment sehr oft durch und ist die Erfolgswahrscheinlichkeit gering, so ist die Poisson-Verteilung eine gute Näherung für die entsprechende Wahrscheinlichkeitsverteilung. Die Poisson-Verteilung wird deshalb manchmal als die Verteilung der seltenen Ereignisse bezeichnet (siehe auch Gesetz der kleinen Zahlen). Zufallsvariablen mit einer Poisson-Verteilung genügen dem Poisson-Prozess.
Die mit Pλ bezeichnete Wahrscheinlichkeitsverteilung wird durch den Parameter
 bestimmt, der gleichzeitig Erwartungswert und Varianz der Verteilung ist. Sie ordnet den natürlichen Zahlen
bestimmt, der gleichzeitig Erwartungswert und Varianz der Verteilung ist. Sie ordnet den natürlichen Zahlen  die Wahrscheinlichkeiten wie folgt zu:
die Wahrscheinlichkeiten wie folgt zu:wobei e die Eulersche Zahl (Basis der natürlichen Exponentialfunktion), λ eine reelle positive Zahl und k! die Fakultät von k bezeichnet.
Die Poisson-Verteilung liefert also Voraussagen über die Anzahl (k) des Eintretens voneinander unabhängiger Ereignisse, die in zufälliger Sequenz innerhalb eines bestimmten Intervalls auftreten, wenn aus vorangehender Beobachtung bereits bekannt ist, wie viele Ereignisse man im Mittel innerhalb dieses Intervalls erwartet (λ). Sie ist ein Spezialfall der Panjer-Verteilung.
Poisson veröffentlichte 1837 seine Gedanken zu dieser Verteilung zusammen mit seiner Wahrscheinlichkeitstheorie in dem Werk „Recherches sur la probabilité des jugements en matières criminelles et en matière civile“ („Untersuchungen zur Wahrscheinlichkeit von Urteilen in Straf- und Zivilsachen“).
Erweiterungen der Poisson-Verteilung wie die Verallgemeinerte Poisson-Verteilung und die Gemischte Poisson-Verteilung werden vor allem im Bereich der Versicherungsmathematik angewendet.
Inhaltsverzeichnis
- 1 Herleitung
- 2 Eigenschaften
- 3 Beziehung zu anderen Verteilungen
- 4 Anwendungsbeispiele
- 5 Zufallszahlen
- 6 Literatur
- 7 Weblinks
Herleitung
Die Poisson-Verteilung ergibt sich einerseits als Grenzfall der Binomial-Verteilung, andererseits lässt sie sich aus grundlegenden Prozesseigenschaften (poissonsche Annahmen) ableiten. Wenn diese Eigenschaften einem Geschehen in guter Näherung zugeordnet werden können, wird die Ereignishäufigkeit Poisson-verteilt sein.
Man betrachtet ein Raum- oder Zeitkontinuum w (das Bernoulli-Experiment wird sehr oft, sozusagen an jedem Punkt des Kontinuums durchgeführt), 'auf' dem zählbare Ereignisse mit konstanter mittlerer Anzahl g pro Einheitsintervall stattfinden. Nun richtet man den Blick auf ein 'genügend' kleines Kontinuumsintervall Δw, das je nach Experiment einen Bereich, ein Zeitintervall, eine abgegrenzte Strecke, Fläche oder Volumen darstellen kann. Was sich dort ereignet, bestimmt die globale Verteilung auf dem Kontinuum.
Die drei poissonschen Annahmen lauten:
- Innerhalb des Intervalls [w,w + Δw] gibt es höchstens ein Ereignis und beliebig viele Momente, in denen nichts geschieht (Seltenheit).
- Die Wahrscheinlichkeit, ein Ereignis im Intervall zu finden, ist proportional zur Länge des Intervalls Δw (g ist konstant und damit auch unabhängig von w).
- Das Eintreten eines Ereignisses im Intervall Δw wird nicht beeinflusst von Ereignissen, die in der Vorgeschichte stattgefunden haben (Geschichtslosigkeit).
Mit Annahme 1 und 2 ist die Wahrscheinlichkeit, ein Ereignis im Intervall Δw zu finden, gegeben als
sowie die Wahrscheinlichkeit eines leeren Intervalls durch
Nach Annahme 3 ist die Wahrscheinlichkeit eines leeren Intervalls Δw unabhängig vom Auftreten irgendwelcher Ereignisse im Bereich w davor. So berechnet man die Wahrscheinlichkeit für kein Ereignis bis zum Punkt w + Δw zu
Das ergibt näherungsweise die Differentialgleichung
 mit der Lösung
mit der Lösungunter der Randbedingung P0(0) = 1. Ebenso findet man die Wahrscheinlichkeit für m Ereignisse bis zum Punkt w + Δw
Jedes angehängte Intervall Δw darf nach Annahme 1 nur entweder kein oder ein Ereignis enthalten. Die entsprechende Differentialgleichung
 hat die Lösung
hat die Lösung .
.
Identifiziert man nun in diesem Ausdruck, der die Wahrscheinlichkeit des Eintretens von m Ereignissen im Kontinuumsbereich w beschreibt, die Parameter
 mit λ und m mit k, stimmt er mit der Formel der Poisson-Verteilung überein. Die Zahl λ ergibt sich in vielen Aufgabenstellungen als Produkt einer Rate (Anzahl von Ereignissen pro Einheitsintervall) und einem Vielfachen des Einheitsintervalls.
mit λ und m mit k, stimmt er mit der Formel der Poisson-Verteilung überein. Die Zahl λ ergibt sich in vielen Aufgabenstellungen als Produkt einer Rate (Anzahl von Ereignissen pro Einheitsintervall) und einem Vielfachen des Einheitsintervalls.Eigenschaften
- Die Poisson-Verteilung Pλ wird durch den Parameter λ vollständig charakterisiert.
- Die Poisson-Verteilung ist stationär, das heißt nicht von der Zeit abhängig.
- In einem Poisson-Prozess ist die zufällige Anzahl der Ereignisse bis zu einem bestimmten Zeitpunkt poissonverteilt, die zufällige Zeit bis zum n-ten Ereignis Erlang-verteilt.
Einfache rekursive Berechnung
Zuerst bestimmt man Pλ(0) = e − λ, dann ergeben sich nacheinander
 Mit wachsendem i werden dabei die Wahrscheinlichkeiten größer, solange i < λ ist. Wird i > λ, schrumpfen sie.
Mit wachsendem i werden dabei die Wahrscheinlichkeiten größer, solange i < λ ist. Wird i > λ, schrumpfen sie.Näherung
Falls bei der Berechnung von
 der Taschenrechner streikt wegen zu großer Werte von λ und k, dann hilft folgende mit der Stirlingformel erhaltene Näherung weiter:
der Taschenrechner streikt wegen zu großer Werte von λ und k, dann hilft folgende mit der Stirlingformel erhaltene Näherung weiter:Verteilungsfunktion
Die Verteilungsfunktion F(x) der Poisson-Verteilung lautet
und gibt die Wahrscheinlichkeit dafür, höchstens n Ereignisse zu finden, wo man λ im Mittel erwartet. Q(a,x) ist die regularisierte Gammafunktion der unteren Grenze.
Erwartungswert, Varianz, Moment
λ ist zugleich Erwartungswert, Varianz und auch drittes zentriertes Moment
 , denn
, dennErwartungswert
Varianz
Alternative Berechnung von Erwartungswert und Varianz
Seien
 unabhängige bernoulliverteilte Zufallsvariablen mit
unabhängige bernoulliverteilte Zufallsvariablen mit  und sei
und sei  . Für
. Für  gilt
gilt  .
.Variationskoeffizient
Aus Erwartungswert und Varianz erhält man sofort den Variationskoeffizienten
 .
.
Schiefe und Wölbung
Die Schiefe ergibt sich zu
 .
.
Die Wölbung lässt sich ebenfalls geschlossen darstellen als
 .
.
Charakteristische Funktion
Die charakteristische Funktion hat die Form
 .
.
Erzeugende Funktion
Für die erzeugende Funktion erhält man
- mX(s) = eλ(s − 1).
Momenterzeugende Funktion
Die momenterzeugende Funktion der Poisson-Verteilung ist
 .
.
Reproduktivität
Die Poisson-Verteilung ist reproduktiv, d.h. die Summe X1 + X2 zweier stochastisch unabhängiger Poisson-verteilter Zufallsvariablen X1 und X2 mit den Parametern λ1 und λ2 ist wieder Poisson-verteilt mit dem Parameter λ1 + λ2. Denn es gilt:
Dies lässt sich auch auf mehrere stochastisch unabhängige Poisson-verteilte Zufallsvariablen
 verallgemeinern. Hier ist
verallgemeinern. Hier ist  .
.Nach einem Satz des sowjetischen Mathematikers D. A. Raikow gilt auch die Umkehrung: Ist eine Poisson-verteilte Zufallsvariable X die Summe von zwei unabhängigen Zufallsvariablen X1 und X2, dann sind die Summanden X1 und X2 ebenfalls Poisson-verteilt. Eine Poisson-verteilte Zufallsvariable lässt sich also nur in Poisson-verteilte unabhängige Summanden zerlegen. Dieser Satz ist ein Analogon zu dem Satz von Cramér für die Normalverteilung.
Die Poisson-Verteilung ist unendlich teilbar.
Symmetrie
Die Poisson-Verteilung Pλ hat für kleine Mittelwerte λ eine stark asymmetrische Gestalt. Für größer werdende Mittelwerte wird Pλ symmetrischer und lässt sich für λ > 30 in guter Näherung durch die Gauß-Verteilung darstellen.
Beziehung zu anderen Verteilungen
Beziehung zur Binomialverteilung
Die Wahrscheinlichkeitsdichte der Binomialverteilung
 lautet
lautetDie Poisson-Verteilung lässt sich aus der Binomialverteilung herleiten. Sie ist die Grenzverteilung der Binomialverteilung bei sehr kleinen Anteilen der interessierten Merkmale und sehr großem Stichprobenumfang:
 und
und  unter der Nebenbedingung, dass das Produkt np = λ konstant ist. λ ist dann für alle in der Grenzwertbildung betrachteten Binomialverteilungen wie auch für die resultierende Poisson-Verteilung der Erwartungswert.
unter der Nebenbedingung, dass das Produkt np = λ konstant ist. λ ist dann für alle in der Grenzwertbildung betrachteten Binomialverteilungen wie auch für die resultierende Poisson-Verteilung der Erwartungswert.Der Wert einer Poisson-verteilten Zufallsvariable an der Stelle k ist der Grenzwert
 einer Binomialverteilung mit
einer Binomialverteilung mit  an der Stelle k:
an der Stelle k:Beziehung zur Normalverteilung
Für große λ kann die Poisson-Verteilung durch die Gaußsche Normalverteilung mit μ = λ und σ2 = λ angenähert werden:
Beziehung zur Erlang-Verteilung
- In einem Poisson-Prozess genügt die zufällige Anzahl der Ereignisse in einem festgelegten Intervall der Poisson-Verteilung
 . Der zufällige Abstand (Strecke oder Zeit) bis zum Eintreffen des n-ten Ereignis hingegen ist
. Der zufällige Abstand (Strecke oder Zeit) bis zum Eintreffen des n-ten Ereignis hingegen ist  Erlang-verteilt. Man sagt auch, dass die Poisson-Verteilung und die Erlang-Verteilung zueinander konjugierte Verteilungen sind. Im Fall n = 1 geht diese Erlang-Verteilung in eine Exponentialverteilung über
Erlang-verteilt. Man sagt auch, dass die Poisson-Verteilung und die Erlang-Verteilung zueinander konjugierte Verteilungen sind. Im Fall n = 1 geht diese Erlang-Verteilung in eine Exponentialverteilung über  . Dabei bezeichnet g die Zahl der erwarteten Ereignisse pro Einheitsintervall.
. Dabei bezeichnet g die Zahl der erwarteten Ereignisse pro Einheitsintervall.  ist dann die Verteilungsdichte des Abstands x, der bis zum Eintreffen des nächsten Ereignisses vergehen wird, wie auch des Abstandes zwischen zwei aufeinanderfolgen Ereignissen.
ist dann die Verteilungsdichte des Abstands x, der bis zum Eintreffen des nächsten Ereignisses vergehen wird, wie auch des Abstandes zwischen zwei aufeinanderfolgen Ereignissen. - Für die Verteilungsfunktionen der Erlang-Verteilung und der Poisson-Verteilung gilt
- FErlang(n + 1) + FPoisson(n) = 1.
Beziehung zur Exponentialverteilung
Der Abstand (räumlich oder zeitlich) bis zum ersten zufälligen Ereignis sowie der Abstand zwischen zwei aufeinanderfolgenden Ereignissen eines Poisson-Prozesses mit dem Parameter
 ist
ist  exponentialverteilt.
exponentialverteilt.Anwendungsbeispiele
Die Poisson-Verteilung ist eine typische Verteilung für die Zahl von Phänomenen, die innerhalb einer Einheit auftreten.
So wird sie häufig dazu benutzt, zeitliche Ereignisse zu beschreiben. Gegeben sind ein zufälliges Ereignis, das durchschnittlich einmal in einem zeitlichen Abstand t1 stattfindet, sowie ein zweiter Zeitraum t2, auf den dieses Ereignis bezogen werden soll.
Die Poisson-Verteilung Pλ(k) mit λ = t2 * 1 / t1 gibt die Wahrscheinlichkeit an, dass im Zeitraum t2 genau k Ereignisse stattfinden. Anders ausgedrückt ist λ die mittlere Auftretenshäufigkeit eines Ereignisses.
Kaufhauskunden
Ein Kaufhaus wird an einem Samstag durchschnittlich alle 10 Sekunden (t1) von einem Kunden betreten. Werden nun im Takt von einer Minute bzw. 60 Sekunden die Personen gezählt, so würde man im Mittel 6 Personen erwarten (λ = 6 Personen/Minute), die das Kaufhaus betreten. P6(k) gibt die Wahrscheinlichkeit dafür an, dass in der nächsten Minute (t2) genau k Kunden das Kaufhaus betreten.
P6(k) k Wahrscheinlichkeit in % Summe in % 0 0,25 0,25 1 1,49 1,74 2 4,46 6,20 3 8,92 15,12 4 13,39 28,51 5 16,06 44,57 6 16,06 60,63 7 13,77 74,40 8 10,33 84,72 9 6,88 91,61 10 4,13 95,74 11 2,25 97,99 12 1,13 99,12 13 0,52 99,64 14 0,22 99,86 15 0,09 99,95 Mit einer Wahrscheinlichkeit von rund 4,5 % betreten genau 2 Personen in einer Minute das Kaufhaus. Mit einer Wahrscheinlichkeit von fast 92 % treten 0 bis 9 Personen (aufsummiert) ein. Die Wahrscheinlichkeit, dass mehr als 9 Personen in einer Minute eintreten, ist folglich 8 %.
Die Werte in der mittleren Spalte ergeben sich jeweils aus dem darüberliegenden Wert, multipliziert mit 6/k.
Radioaktiver Zerfall
In der Natur folgt zum Beispiel die Anzahl radioaktiver Zerfälle einzelner Atome in einem gegebenen Zeitintervall, dessen Dauer die Annahme einer konstanten Zerfallswahrscheinlichkeit rechtfertigt, der Poisson-Statistik. Umgekehrt sind dementsprechend die Zeiten zwischen einzelnen Zerfallsereignissen exponentialverteilt.
Zählexperiment
Die Messung einer poisson-verteilten Anzahl von Ereignissen wird bei häufiger Wiederholung um den gemessenen Mittelwert
 mit Standardabweichung
mit Standardabweichung  streuen. Wird nur einmal (ohne Wiederholen des Experiments) gezählt, dient das Ergebnis
streuen. Wird nur einmal (ohne Wiederholen des Experiments) gezählt, dient das Ergebnisals bester Schätzer für Mittelwert (n) der zugrunde liegenden Poisson-Verteilung sowie Unsicherheit
 (Standardabweichung) der erhaltenen Anzahl. Um hier relative Genauigkeit von 1 % zu erzielen, braucht man also 'hohe Stastistik' von über 10000 Ereignissen!
(Standardabweichung) der erhaltenen Anzahl. Um hier relative Genauigkeit von 1 % zu erzielen, braucht man also 'hohe Stastistik' von über 10000 Ereignissen!Blitzeinschläge
Die Blitzhäufigkeit in Deutschland beträgt 10 Einschläge pro km² = 0,1 Einschläge pro ha und Jahr. Wie groß ist die Wahrscheinlichkeit, dass es in einer Parzelle von 1 ha zu k Blitzeinschlägen in einem Jahr kommt?
λ = 0,1 Einschläge pro Hektar und Jahr.
- P0,1(k = 0) (kein Einschlag im betrachteten Jahr): 90 %
- P0,1(k = 1) (ein Einschlag im betrachteten Jahr): 9 %
- P0,1(k = 2) (zwei Einschläge im betrachteten Jahr): 0,5 %
- P0,1(k = 3) (drei Einschläge im betrachteten Jahr): 0,02 %
Statistisch ist es nicht verwunderlich, wenn ein Blitz innerhalb von 200 Jahren zweimal am gleichen Ort einschlägt, wobei es außerordentlich unwahrscheinlich ist, den Ort voraussagen zu können (Siehe hierzu auch Geburtstagsparadoxon).
Verstreute Reiskörner
Das Bild rechts zeigt N = 66 Reiskörner, die zufällig auf n = 49 Quadrate verteilt wurden. Die Felder enthalten
 Reiskörner. Der Vergleich zwischen Experiment und berechneter Poisson-Verteilung P(X = k), wobei λ = N / n = 66 / 49 = 1,35 Reiskörner/Quadrate ist, zeigt eine gute Übereinstimmung:
Reiskörner. Der Vergleich zwischen Experiment und berechneter Poisson-Verteilung P(X = k), wobei λ = N / n = 66 / 49 = 1,35 Reiskörner/Quadrate ist, zeigt eine gute Übereinstimmung:k gezählt 
0
15
12,7
1
15
17,2
2
11
11,6
3
5
5,2
4
1
1,7
5
2
0,5
Die Wahrscheinlichkeit, dass ein bestimmtes Feld leer bleibt, ist etwa 26 %:

Sportergebnisse
Die (zeitliche) Konstanz der Ereigniswahrscheinlichkeit - eine wesentliche Voraussetzung für die Anwendung der Poissonstatistik (siehe oben unter Poissonsche Annahmen) - ist bei Sportergebnissen natürlich höchstens näherungsweise gegeben. Es wirken viele im Einzelnen nicht isolierbare Einflüsse zusammen und ergeben eine Wahrscheinlichkeit für Punkte oder Tore, die man ohne besseres Wissen eben als konstant annimmt. Auch ob z.B. Tore unabhängig voneinander fallen, ist fraglich. Das Zutreffen dieser Annahmen lässt sich aber im Nachhinein an der Übereinstimmung von Daten und Poissonverteilung testen. Hier gibt es einen 'Spielraum' und keine Eindeutigkeit.
In vielen Sportarten geht es zum Siegen in einem Wettbewerb darum, innerhalb eines bestimmten Zeitraums mehr zählende Ereignisse zu erwirken, als der Gegner.
Die durchschnittliche Anzahl von Toren pro Spiel und Mannschaft betrug während der Gruppenphase der Fußball-Weltmeisterschaft 2010 der Herren in Südafrika 1,05 (101 Tore in 48 Spielen). Mit diesem Wert können mit Hilfe der Poisson-Verteilung die Verteilung der Tore und die Verteilung der Endergebnisse der Begegnungen berechnet werden. Die Wahrscheinlichkeit für ein bestimmtes Endergebnis ergibt sich hierbei aus dem Produkt der Wahrscheinlichkeiten der beiden Gegner für die entsprechenden Torerfolge. Auch hier ist die Summe aller Wahrscheinlichkeiten 100 %.
Die folgende Tabelle zeigt die berechneten Anteile der Endergebnisse auf der linken Seite und die tatsächlichen Anteile der Endergebnisse auf der rechten Seite. Die Übereinstimmung ist gut, und die Abweichungen zwischen tatsächlichen und berechneten Ergebnissen für einen bestimmten Spielendstand sind weit unten im einstelligen Prozentbereich. Ein Spiel entspricht einem Anteil von 1/48 (= 2,083 %) aller Spiele. In nur einem Fall (Endergebnis 0:1) beträgt die Abweichung zwischen der Berechnung und der tatsächlichen Anzahl von Spielen 2 (oder 3,81 %), in allen anderen Fällen ist sie maximal eins.
Tore
(Parameter k)berechnet 0 1 2 3 4 geschossen 0 1 2 3 4 Differenz 0 1 2 3 4 P
(λ = 1,05)35 % 37 % 19 % 7 % 2 % 0 35 % 12 % 13 % 7 % 2 % 1 % 13 % 17 % 6 % 4 % 0 % -1 % -4 % 1 % -2 % 1 % 1 37 % 13 % 14 % 7 % 2 % 1 % 10 % 13 % 8 % 2 % 0 % 3 % 1 % -1 % 0 % 1 % 2 19 % 7 % 7 % 4 % 1 % 0 % 6 % 6 % 4 % 0 % 0 % 1 % 1 % 0 % 1 % 0 % 3 7 % 2 % 2 % 1 % 0 % 0 % 0 % 2 % 2 % 0 % 0 % 2 % 0 % -1 % 0 % 0% 4 2 % 1 % 1 % 0 % 0 % 0 % 2 % 2 % 0 % 0 % 0 % -1 % -1 % 0 % 0 % 0 % 5 0 % 0 % 0 % 0 % 0 % 0 % 0 % 0 % 0 % 0 % 0 % 0 % 0 % 0 % 0 % 0 % 6 0 % 0 % 0 % 0 % 0 % 0 % 0 % 0 % 0 % 0 % 0 % 0 % 0 % 0 % 0 % 0 % 7 0 % 0 % 0 % 0 % 0 % 0 % 2 % 0 % 0 % 0 % 0 % -2 % 0 % 0 % 0 % 0 % Grenzwertüberschreitung
Die Anzahl nup poissonverteilter Ereignisse, die mit vorgegebener Wahrscheinlichkeit p < 1 nicht überschritten wird, lässt sich aus der Inversion der Verteilungsfunktion berechnen:
Nun ist keine elementare Form der Inversion der Verteilungsfunktion, bezogen auf ihr erstes Argument, bekannt. Außer dem punktweisen Berechnen der Inversion gibt es aber noch folgende Möglichkeit:
Man findet für λ > 0,15, dass zum Beispiel folgende Ausdrücke der Verteilungsfunktion kaum (< 1 %) von λ abhängen:
Allgemein liegt für hohe Werte von p > 0,9 die Verteilungsfunktion
 sehr nahe bei p, wobei xp das einseitige Quantil der Standardnormalverteilung darstellt und xp als Funktion der Wahrscheinlichkeit p durch
sehr nahe bei p, wobei xp das einseitige Quantil der Standardnormalverteilung darstellt und xp als Funktion der Wahrscheinlichkeit p durch  bestimmt ist. Die rechte Seite der Gleichung für xp entsteht aus der Umkehrfunktion des Fehlerintegrals Φ(xp). Eine auch für den Taschenrechner geeignete Näherung (bei p > 0,95 besser als 0,5 %) liefert
bestimmt ist. Die rechte Seite der Gleichung für xp entsteht aus der Umkehrfunktion des Fehlerintegrals Φ(xp). Eine auch für den Taschenrechner geeignete Näherung (bei p > 0,95 besser als 0,5 %) liefert  mit
mit 
Der Ansatz für g(λ) in
 ist zunächst motiviert durch die Tatsache, dass die Poisson-Verteilung für große λ in eine Normalverteilung mit Obergrenze
ist zunächst motiviert durch die Tatsache, dass die Poisson-Verteilung für große λ in eine Normalverteilung mit Obergrenze  übergeht. Das zusätzliche
übergeht. Das zusätzliche  verbessert die Konstanz der Verteilungsfunktion bei kleinem λ.
verbessert die Konstanz der Verteilungsfunktion bei kleinem λ.Für Mittelwerte λ < 0,15 wird mit Wahrscheinlichkeit p = 0,99 (99 %) maximal 1 Ereignis auftreten. Ist λ größer, dann berechnet sich die mit Wahrscheinlichkeit p zu erwartende größte Häufigkeit von Ereignissen nup in guter Näherung aus der einfachen Formel
Bei deutlich nicht ganzzahligem Ergebnis empfiehlt es sich aufzurunden. Damit wird bei vielfachen Wiederholungen (oder anders formuliert: auf lange Sicht) die Wahrscheinlichkeit, mit der Zahl der Ereignisse unter der Grenze zu bleiben, etwas erhöht. Mit p = 0,95 (entspricht xp = 1,645) und λ = 6 sind also nicht mehr als nup = 10 Ereignisse zu erwarten.
Zufallszahlen
Zufallszahlen zur Poisson-Verteilung werden üblicherweise mit Hilfe der Inversionsmethode erzeugt.
Literatur
- Erich Härtter: Wahrscheinlichkeitsrechnung für Wirtschafts- und Naturwissenschaftler. Vandenhoeck und Ruprecht, Göttingen 1974, ISBN 3-525-03114-9
- Frodesen, Skjeggestad, Tofte: Probability and Statistics in Particle Physics, Universitetsforlaget, Bergen - Oslo - Tromsö
Weblinks
 Wikibooks: Poissonverteilung (für Anfänger) – Lern- und Lehrmaterialien
Wikibooks: Poissonverteilung (für Anfänger) – Lern- und Lehrmaterialien- Universität Konstanz – Interaktive Animation
- StatWiki – Herleitung der momenterzeugenden Funktion
- PoissonDiagrammer – Programm zum zeichnen der Poisson-Verteilung(auch für hohe Erwartungswerte)
Diskrete univariate VerteilungenDiskrete univariate Verteilungen für endliche Mengen:
Benford | Bernoulli | beta-binomial | binomial | kategorial | hypergeometrisch | Rademacher | Zipf | Zipf-MandelbrotDiskrete univariate Verteilungen für unendliche Mengen:
Boltzmann | Conway-Maxwell-Poisson | negativ binomial | erweitert negativ binomial | Compound-Poisson | diskret uniform | discrete-Phase-Type | Gauss-Kuzmin | geometrisch | logarithmisch | parabolisch-fraktal | Poisson | Poisson-Gamma | Skellam | Yule-Simon | Zeta
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
Poisson Verteilung — Die Poisson Verteilung ist eine diskrete Wahrscheinlichkeitsverteilung, die beim mehrmaligen Durchführen eines Bernoulli Experiments entsteht. Letzteres ist ein Zufallsexperiment, das nur zwei mögliche Ergebnisse besitzt (z. B. „Erfolg“ und… … Deutsch Wikipedia
Poisson-Verteilung — I Poisson Verteilung [pwa sɔ̃ ; nach S. D. Poisson], Grenzfall der Binomialverteilung B (n, p), bei der die Wahrscheinlichkeit p eines bestimmten Ereignisses sehr klein, die Anzahl n der unabhängigen Wiederholungen aber sehr groß ist (»Gesetz… … Universal-Lexikon
Poisson-Verteilung — Puasono skirstinys statusas T sritis Standartizacija ir metrologija apibrėžtis Retų įvykių skirstinys. atitikmenys: angl. Poisson distribution vok. Poissonsche Verteilung, f; Poisson Verteilung, f rus. распределение Пуассона, n pranc.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
Poisson-Verteilung — Puasono skirstinys statusas T sritis fizika atitikmenys: angl. Poisson distribution vok. Poissonsche Verteilung, f; Poisson Verteilung, f rus. распределение Пуассона, n pranc. distribution de Poisson, f … Fizikos terminų žodynas
Gemischte Poisson-Verteilung — Die gemischte Poisson Verteilung ist eine diskrete Wahrscheinlichkeitsverteilung, die als allgemeiner Ansatz für die Schadenzahlverteilung in der Versicherungsmathematik zu finden ist. Sie verallgemeinert die Poisson Verteilung.… … Deutsch Wikipedia
Verallgemeinerte Poisson-Verteilung — Die verallgemeinerte Poisson Verteilung ist eine diskrete Wahrscheinlichkeitsverteilung, die vor allem in der Versicherungsmathematik verwendet wird. Im Vergleich zur Poisson Verteilung besitzt sie zwei Parameter, ist dadurch wesentlich flexibler … Deutsch Wikipedia
Poisson — ist der Name von David Poisson (* 1982), französischer Skirennläufer Georges Poisson (* 1924), Architektur und Literaturhistoriker Jeanne Antoinette Poisson, marquise de Pompadour (1721–1764), „Madame de Pompadour“ Siméon Denis Poisson… … Deutsch Wikipedia
Poisson — [pwa sɔ̃], Siméon Denis, französischer Mathematiker und Physiker, * Pithiviers (Département Loiret) 21. 6. 1781, ✝ Paris 25. 4. 1840; ab 1800 an der École Polytechnique (1806 Professor). Poisson stellte eine von der laplaceschen abweichende… … Universal-Lexikon
Poisson-Prozess — [pwa sɔ̃ ; nach S. D. Poisson], punktueller stochastischer Prozess, bei dem die Wahrscheinlichkeit eines Ereignisses innerhalb eines beliebigen Zeitintervalls durch die Poisson Verteilung gegeben ist; die Wahrscheinlichkeiten in nicht… … Universal-Lexikon
Poisson Statistik — Die Poisson Verteilung ist eine diskrete Wahrscheinlichkeitsverteilung, die beim mehrmaligen Durchführen eines Bernoulli Experiments entsteht. Letzteres ist ein Zufallsexperiment, das nur zwei mögliche Ergebnisse besitzt (z. B. „Erfolg“ und… … Deutsch Wikipedia