- Polygonmethode
-
Mit Thiessen-Polygonen bzw. Voronoi-Diagramm oder Dirichlet-Zerlegung wird eine Zerlegung des Raumes in Regionen bezeichnet, die durch eine vorgegebene Menge an Punkten des Raumes, hier als Zentren bezeichnet, bestimmt werden. Jede Region wird durch genau ein Zentrum bestimmt und umfasst alle Punkte des Raumes, die in Bezug zur euklidischen Metrik näher an dem Zentrum der Region liegen, als an jedem anderen Zentrum. Aus allen Punkten, die mehr als ein nächstgelegenes Zentrum besitzen und somit die Grenzen der Regionen bilden, entsteht das Voronoi-Diagramm. Derartige Regionen werden auch als Voronoi-Regionen bezeichnet.
Voronoi-Diagramme werden in verschiedensten wissenschaftlichen Bereichen wie der Biologie, Chemie, Meteorologie, Kristallographie und anderen wissenschaftlichen Disziplinen wie der Algorithmischen Geometrie und der Materialwissenschaft verwendet. Obwohl 1644 schon durch Descartes in seinem Buch Principia Philosophiae erwähnt, erfuhren sie erstmals durch Dirichlet und Voronoi eine genauere mathematische Analyse.[1] Voronoi-Diagramme können durchaus auch als Zerlegung hochdimensionaler Räume verwendet werden. In der Literatur ist die Definition meist auf den zweidimensionalen reellen Raum beschränkt.
Inhaltsverzeichnis
Definition
Die Thiessen-Polygone oder das Voronoi-Diagramm besteht aus dem gesamten Raum abzüglich der Voronoi-Regionen, welche in Bezug auf den euklidischen Abstand aus allen Punkten des Raumes entsteht, die näher am korrespondierenden Zentrum liegen als an allen anderen Zentren. Diese können im zweidimensionalen als Schnitt mehrerer offener Halbebenen betrachtet werden, welche wiederum durch einen Bisektor zwischen je zwei Punkten der Zentren begrenzt werden.
Formal ist eine Voronoi-Region VR(p,S) des Punktes
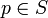 , wobei S eine vorgegebene Menge an Punkten des
, wobei S eine vorgegebene Menge an Punkten des 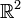 ist, gegeben durch
ist, gegeben durch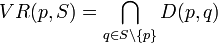 ,
,wobei D(p,q) als offene Halbebene definiert ist und durch
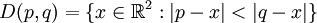
gegeben ist. Sind nun alle Voronoi-Regionen durch
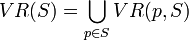
gegeben, erhält man das Voronoi-Diagramm durch
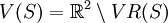
Informell bedeutet das, dass genau die Grenzen der Regionen, welche selbst nicht zu diesen dazu gehören, das Diagramm bzw. die Polygone bilden. Die resultierenden Polygone können in Voronoi-Kanten (Kanten des Polygons) und Voronoi-Knoten (Ecken des Polygons) eingeteilt werden.
Dualität
Das Voronoi-Diagramm verhält sich dual zur Delaunay-Triangulation und wird zur Konstruktion einer entsprechend triangulisierten Oberfläche verwendet. Um die Delaunay-Triangulation zu berechnen, wird der entsprechende duale Graph zum Voronoi-Diagramm gebildet. Dies geschieht, indem die Zentren der Polygone derart miteinander verbunden werden, so dass zu jeder Voronoi-Kante eine orthogonale Linie eingezeichnet wird, die die entsprechenden zwei Zentren miteinander verbindet (siehe Abbildung).
Polygon-Methode
Thiessen-Polygone werden unter anderem bei der kartographischen Darstellung von Messwerten eingesetzt. Die Polygon-Methode ist ein nichtstatistisches (d.h. vergleichsweise einfaches) Interpolationsverfahren der Geostatistik zur einfachen Darstellung der räumlichen Verteilung georeferenzierter Messdaten.
Als Grundannahme gilt, dass die Ähnlichkeit des unbekannten Wertes eines Punktes in der Fläche zum bekannten Messwert mit der Entfernung von diesem abnimmt, die Daten also umso unähnlicher sind, je weiter sie auseinander liegen. Dieser Zusammenhang wird bei der Polygon-Methode dadurch zum Ausdruck gebracht, dass jeder Messwert für ein ihn umgebendes Thiessen-Polygon homogenisiert wird, also alle Schätzwerte innerhalb dieses Polygons identisch zum jeweiligen Messwert sind.
Das Verfahren bildet insofern eine schlechte Näherung an die beobachtbare Realität, da an den Polygongrenzen scharfe Wertesprünge auftreten; fließende Übergänge zwischen zwei Messwerten können mit dieser Methode also nicht dargestellt werden.
Weblinks
- Applet zur Berechnung und Visualisierung der konvexen Hülle, Delaunay-Triangulation und des Voronoi-Diagramms im Raum
- MathWorld (englisch)
- Eine ganze Website zu Voronoi-Diagrammen (englisch)
- Java-Applet für Voronoi-Diagramme
- Weiteres Java-Applet
- Zelluläre Raumstruktur, mit Hilfe von Voronoi generiert (englisch)
- Java-Applet, das die Konstruktion eines Voronoi-Diagramms im Sweep-Line-Verfahren demonstriert
- [1]
- Konstruktion abstrakter Voronoi-Diagramme in O(n log n), Ronny Harbich, 2007
Einzelnachweise
- ↑ Prof. Dr. Rolf Klein, Algorithmische Geometrie, Springer Verlag (2005), ISBN 978-3-540-20956-0
Wikimedia Foundation.


