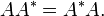- Quasinormaler Operator
-
In der Funktionalanalysis verallgemeinert der normale Operator den Begriff der normalen Matrix aus der linearen Algebra. Ist X ein Hilbertraum, so heißt ein Operator
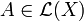 normal, falls er mit seiner Adjungierten
normal, falls er mit seiner Adjungierten 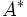 kommutiert, d.h. wenn
kommutiert, d.h. wennDabei bezeichnet
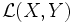 die Menge aller stetigen linearen Abbildungen von X nach Y und
die Menge aller stetigen linearen Abbildungen von X nach Y und 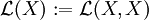 die Menge der stetigen Endomorphismen von X.
die Menge der stetigen Endomorphismen von X.Eigenschaften
Sei
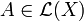 ein normaler Operator. Dann gilt:
ein normaler Operator. Dann gilt: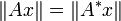 für alle
für alle 
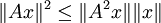 für alle
für alle 
- Operatornorm = Spektralradius, d.h.:
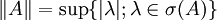
- Die von A erzeugte C*-Algebra und die von A erzeugte Von-Neumann-Algebra sind kommutativ. Dieser Sachverhalt ermöglicht einen Funktionalkalkül.
- Die Diagonalisierbarkeit normaler Matrizen in der linearen Algebra verallgemeinert sich auf normale Operatoren in Form des Spektralsatzes.
- Eine Klassifikation normaler Operatoren besteht bzgl. unitärer Äquivalenz modulo kompakter Operatoren, indem man zur Calkin-Algebra übergeht, die im endlich-dimensionalen Fall {0} ist. Das ist im Artikel zur Calkin-Algebra ausgeführt.
Verwandte Begriffe
Ein Operator
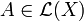 heißt
heißt- quasinormal, falls
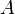 mit
mit 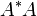 vertauscht, das heißt
vertauscht, das heißt 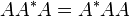 .
. - subnormal, falls es einen Hilbertraum Y gibt, so dass X unterraum von Y ist, und einen normalen Operator
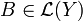 , so dass
, so dass 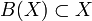 und
und 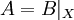
- hyponormal, falls
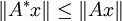 für alle
für alle  .
. - paranormal, falls
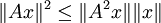 für alle
für alle  .
. - normaloid, falls Operatornorm = Spektralradius, d.h.:
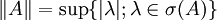 .
.
Es gelten folgende Implikationen:
normal
 quasinormal
quasinormal  subnormal
subnormal  hyponormal
hyponormal  paranormal
paranormal  normaloid.
normaloid.Literatur
- Harro Heuser: Funktionalanalysis. B.G. Teubner, Stuttgart (1986), 3-519-22206-X.
Wikimedia Foundation.