Aussagenverknüpfung

In der (formalen) Logik bezeichnet man eine Aussage V, die mit Hilfe von Formulierungen wie „und“, „oder“, „wenn–dann“ und „es ist nicht der Fall, dass“ aus anderen Aussagen zusammengesetzt ist, als komplexe Aussage, zusammengesetzte Aussage oder als Aussagenverknüpfung (Verknüpfung von Aussagen, logische Verknüpfung). Die Formulierungen, mit deren Hilfe Aussagen zu komplexen Aussagen verbunden werden, werden als Junktoren, Konnektive, Verknüpfungszeichen oder ebenfalls als Aussagenverknüpfung beziehungsweise Logische Verknüpfung bezeichnet. Eine Aussage, die nicht aus anderen Aussagen zusammengesetzt ist, wird atomare Aussage genannt.

Beispiel: Wenn Anna Urlaub hat, dann fährt sie ans Meer.

Im einfachsten Fall, insbesondere in der klassischen Aussagenlogik lässt sich die Bedeutung eines Junktors durch eine Wahrheitswertetabelle definieren. Für den Fall, dass zwei Aussagen, A und B, verknüpft werden, gibt es genau 16 verschiedene Möglichkeiten, eine Verknüpfung zu definieren. In der folgenden Tabelle sind alle 16 möglichen Verknüpfungen von $V 1$ bis $V 16$ aufgeführt:

V 1

V 2

V 3

V 4

V 5

V 6

V 7

V 8

V 9

V 10

V 11

V 12

V 13

V 14

V 15

V 16

Die einzelnen Verknüpfungen haben alle besondere Namen, die in der weiteren Tabelle dargestellt sind:

Verknüpfung	Formel	Name
$V 1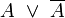$	$A ~ \or ~ \overline{A}$	Tautologie
$V 2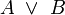$	$A ~ \or ~ B$	(einschließende) Disjunktion, Adjunktion
$V 3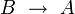$	$B ~\rightarrow ~ A$	Konversion
$V 4$	A	Identität von A
$V 5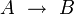$	$A ~\rightarrow ~ B$	materiale Implikation, Konditional Subjunktion
$V 6$	B	Identität von B
$V 7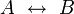$	$A ~\leftrightarrow ~ B$	Bikonditional, Bijunktion
$V 8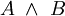$	$A ~ \and ~ B$	Konjunktion
$V 9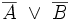$	$~ \overline{A} ~ \or ~ \overline{B}$	Sheffer-Funktion
$V 10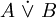$	$A ~ \dot\or ~ B$	ausschließende Disjunktion, XOR
$V 11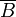$	$\overline{B}$	Negation von B
$V 12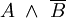$	$A ~ \and ~ \overline{B}$	Nur A
$V 13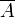$	$\overline{A}$	Negation von A
$V 14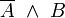$	$~ \overline{A} ~ \and ~ B$	Nur B
$V 15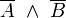$	$~ \overline{A} ~ \and ~ \overline{B}$	Peirce-Funktion, NOR
$V 16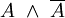$	$A ~ \and ~ \overline{A}$	Kontradiktion

Es ist möglich, einzelnen Verknüpfungen durch andere auszudrücken; zum Beispiel lässt sich die Konjunktion 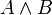$A \and B$ durch Disjunktion und Negation als 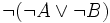$\neg (\neg A \or \neg B)$ ausdrücken. Wenn eine Menge von Verknüpfungen in der Lage ist, alle anderen Verknüpfungen auszudrücken, dann heißt diese Menge funktional vollständig. Tatsächlich ist es möglich ist, alle Verknüpfungen allein mit Hilfe einer einzigen Verknüpfung darzustellen, und zwar mit der Verknüpfung $V 9$ (Shefferfunktion, NAND), aber auch mit der Verknüpfung $V 15$ (Peirce-Funktion, NOR).

Wikimedia Foundation.

Игры ⚽ Поможем написать реферат

Schlagen Sie auch in anderen Wörterbüchern nach:

Aussage (Logik) — Eine Aussage im aristotelischen Sinn ist ein sprachliches Gebilde, von dem es sinnvoll ist zu fragen, ob es wahr oder falsch ist (so genanntes Aristotelisches Zweiwertigkeitsprinzip). Es ist nicht erforderlich, sagen zu können, ob das Gebilde… … Deutsch Wikipedia
Ausdruck (Logik) — Eine Aussage im aristotelischen Sinn ist ein sprachliches Gebilde, von dem es sinnvoll ist zu fragen, ob es wahr oder falsch ist (so genanntes Aristotelisches Zweiwertigkeitsprinzip). Es ist nicht erforderlich, sagen zu können, ob das Gebilde… … Deutsch Wikipedia
Logische Aussage — Eine Aussage im aristotelischen Sinn ist ein sprachliches Gebilde, von dem es sinnvoll ist zu fragen, ob es wahr oder falsch ist (so genanntes Aristotelisches Zweiwertigkeitsprinzip). Es ist nicht erforderlich, sagen zu können, ob das Gebilde… … Deutsch Wikipedia
Logischer Ausdruck — Eine Aussage im aristotelischen Sinn ist ein sprachliches Gebilde, von dem es sinnvoll ist zu fragen, ob es wahr oder falsch ist (so genanntes Aristotelisches Zweiwertigkeitsprinzip). Es ist nicht erforderlich, sagen zu können, ob das Gebilde… … Deutsch Wikipedia
Junktor — Junktoren (von lat. iungere „verknüpfen, verbinden“) sind Verknüpfungen zwischen Aussagen innerhalb der Aussagenlogik, also logische Operatoren. Sie werden auch Konnektive, Konnektoren, Satzoperatoren, Satzverknüpfer, Satzverknüpfungen,… … Deutsch Wikipedia
Adjungiert — Das Wort Adjunktion (lat. adiunctio Anknüpfung , Hinzufügung , vereinigende Verknüpfung ) wird in der Mathematik in verschiedenen Zusammenhängen benutzt: Die älteste mathematische Verwendung ist die wörtliche in der Logik: adiunctio , also… … Deutsch Wikipedia
Atom (Logik) — Als atomare Aussagen (auch Atomaussagen, Aussagenatom, Atome, Primaussagen, einfache Aussage, unzusammengesetzte Aussage, elementare Aussage, Elementaraussage, elementarer Satz, Elementarsatz, Atomsatz) werden in der mathematischen oder formalen… … Deutsch Wikipedia
Atomare Aussage — Als atomare Aussagen (auch Atomaussagen, Aussagenatom, Atome, Primaussagen, einfache Aussage, unzusammengesetzte Aussage, elementare Aussage, Elementaraussage, elementarer Satz, Elementarsatz, Atomsatz) werden in der mathematischen oder formalen… … Deutsch Wikipedia
Adjunktion — Das Wort Adjunktion (lat. adiunctio Anknüpfung , Hinzufügung , vereinigende Verknüpfung ) wird in der Mathematik in verschiedenen Zusammenhängen benutzt: Die älteste mathematische Verwendung ist die wörtliche in der Logik: adiunctio , also… … Deutsch Wikipedia
Antezedens und Sukzedens — Eine Implikation (von lat. implicare, „einwickeln“) bezeichnet: bildungssprachlich die Einbeziehung einer Sache in eine andere; ein mitgemeinter, aber nicht explizit ausgedrückter Bedeutungsinhalt. In der Logik die Verknüpfung von Aussagen a und… … Deutsch Wikipedia

Academic dictionaries and encyclopedias

Aussagenverknüpfung

Schlagen Sie auch in anderen Wörterbüchern nach:

Share the article and excerpts

Academic dictionaries and encyclopedias

Deutsch Wikipedia

Aussagenverknüpfung

Schlagen Sie auch in anderen Wörterbüchern nach:

Share the article and excerpts

Direct link