- Funktionale Vollständigkeit
-
Junktoren (von lat. iungere „verknüpfen, verbinden“) sind Verknüpfungen zwischen Aussagen innerhalb der Aussagenlogik, also logische Operatoren. Sie werden auch Konnektive, Konnektoren, Satzoperatoren, Satzverknüpfungen, Aussagenverknüpfer, logische Bindewörter, Verknüpfungszeichen oder Funktoren genannt und als logische Partikel klassifiziert.
Sprachlich wird zwischen der jeweiligen Verknüpfung selbst (zum Beispiel der Konjunktion) und dem sie bezeichnenden Wort beziehungsweise Sprachzeichen (zum Beispiel dem Wort „und“ beziehungsweise dem Zeichen „∧“) oft nicht unterschieden.
In Programmiersprachen werden ebenfalls aussagenlogische Junktoren verwendet, die sich aber in wesentlichen Punkten von den üblichen aussagenlogischen Junktoren unterscheiden. Sie werden dort überwiegend als logische Operatoren bezeichnet.
Inhaltsverzeichnis
Extensionale Junktoren
Man nennt einen Junktor wahrheitsfunktional oder extensional, wenn der Wahrheitswert eines durch ihn gebildeten zusammengesetzten Satzes eindeutig durch die Wahrheitswerte seiner Teilsätze bestimmt ist. Ein logisches System, das ausschließlich extensionale Junktoren umfasst, heißt extensional. Die klassische Logik ist extensional.
Für eine genauere Definition von Extensionalität siehe Extensionalitätsprinzip.
Wahrheitstafeln
Eine Methode, den Wahrheitswertverlauf extensionaler Junktoren in einer Logik mit endlich vielen Wahrheitswerten übersichtlich darzustellen, sind die sogenannten Wahrheitstafeln. Bei diesen wird für eine mittels des Junktors aus einfachen Einzelaussagen gebildete zusammengesetzte Gesamtaussage für jede mögliche Zuordnung von Wahrheitswerten zu den Einzelaussagen der Wahrheitswert der Gesamtaussage angegeben. Für einen zweistelligen Junktor einer zweistelligen Logik könnte eine Wahrheitstafel wie folgt aussehen:
Wahrheitstafel für einen zweistelligen Junktor einer zweiwertigen Logik A B A op B W W Wahrheitswert von „A op B“, wenn sowohl A als auch B wahr ist W F Wahrheitswert von „A op B“, wenn A wahr und B falsch ist F W Wahrheitswert von „A op B“, wenn A falsch und B wahr ist F F Wahrheitswert von „A op B“, wenn sowohl A als auch B falsch ist Stelligkeit
Die Anzahl der Aussagen, die (beziehungsweise mit denen sich) ein Junktor zu einer neuen Aussage verknüpft, nennt man seine Stelligkeit: Ein einstelliger Junktor verbindet sich mit einer einzigen Aussage zu einer neuen Aussage, zweistellige Junktoren verbinden sich mit zwei Aussagen zu einer neuen Aussage und so weiter. Allgemein verbindet ein n-stelliger Junktor sich mit n Aussagen zu einer neuen.
Die Stelligkeit ist nicht zu verwechseln mit der Wertigkeit, d. h. mit der Frage, wieviele Wahrheitswerte zugelassen werden (vgl. Bivalenzprinzip).
In der klassischen Logik ist der wichtigste einstellige Junktor die Negation und sind wichtige zweistellige Junktoren (oft werden nur diese beiden verwendet) die Konjunktion und die Disjunktion. Ebenso lassen sich klassische drei- und mehrstellige Junktoren auf Kombinationen ein- und zweistelliger Junktoren zurückführen.
Junktoren der klassischen Aussagenlogik
Allgemein gibt es für eine m-wertige Logik, d. h. für eine Logik mit endlich vielen Wahrheitswerten, deren Anzahl m ist,
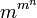 n-stellige wahrheitsfunktionale Junktoren. Für die zweiwertige Aussagenlogik gibt es also
n-stellige wahrheitsfunktionale Junktoren. Für die zweiwertige Aussagenlogik gibt es also 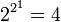 einstellige Junktoren und
einstellige Junktoren und 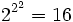 zweistellige Junktoren. Schon für die dreiwertige Aussagenlogik gibt es
zweistellige Junktoren. Schon für die dreiwertige Aussagenlogik gibt es 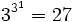 einstellige und
einstellige und 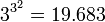 zweistellige Junktoren.
zweistellige Junktoren.Die sechzehn zweistelligen Junktoren der zweiwertigen Logik sind in nachfolgender Tabelle dargestellt.
-
Junktorentafel der zweistelligen Junktoren Nummer Wahrheitswerte Name Symbole 0 F F F F Kontradiktion 
1 W F F F Konjunktion 
2 F W F F Postsektion  ,
, 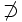
3 W W F F Präpendenz 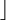
4 F F W F Präsektion 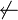 ,
, 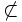
5 W F W F Postpendenz 
6 F W W F Kontravalenz 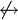 ,
, 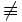 ,
, 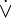 ,
, 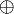
7 W W W F Disjunktion 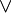
8 F F F W Peirce-Funktion 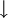
9 W F F W Bikonditional 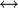
10 F W F W Postnonpendenz 
11 W W F W Replikation 
12 F F W W Pränonpendenz 
13 W F W W Konditional 
14 F W W W Sheffer-Funktion 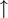
15 W W W W Tautologie 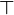
Reduzierbarkeit der Junktorenmenge, funktionale Vollständigkeit und Sheffer-Operatoren
Einzelne Junktoren lassen sich durch andere Junktoren ausdrücken, z. B. kann man für die klassische Logik das Konditional
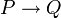 durch die Disjunktion
durch die Disjunktion 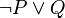 ausdrücken. Allgemein heißt eine Menge von Junktoren bezogen auf ein logisches System funktional vollständig oder semantisch vollständig, wenn mit Hilfe der betroffenen Konnektive alle anderen Konnektive des logischen Systems ausgedrückt werden können. Für die klassische Aussagenlogik sind zum Beispiel die Junktorenmengen {
ausdrücken. Allgemein heißt eine Menge von Junktoren bezogen auf ein logisches System funktional vollständig oder semantisch vollständig, wenn mit Hilfe der betroffenen Konnektive alle anderen Konnektive des logischen Systems ausgedrückt werden können. Für die klassische Aussagenlogik sind zum Beispiel die Junktorenmengen { ,
, 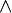 }, {
}, { ,
, 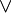 } und {
} und { ,
,  } funktional vollständig. Das bedeutet, dass sich alle Junktoren der klassischen Aussagenlogik wahlweise auf Negation und Konjunktion, auf Negation und Disjunktion oder auf Negation und Konditional zurückführen lassen. Häufig verwendete Junktorenmengen sind {
} funktional vollständig. Das bedeutet, dass sich alle Junktoren der klassischen Aussagenlogik wahlweise auf Negation und Konjunktion, auf Negation und Disjunktion oder auf Negation und Konditional zurückführen lassen. Häufig verwendete Junktorenmengen sind { ,
, 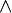 ,
, 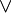 }, {
}, {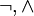 }, {
}, {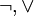 } und {
} und {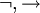 }.
}.Wenn sich mit einem Junktor allein, d. h. ganz ohne Hinzunahme weiterer Junktoren alle anderen Junktoren ausdrücken lassen, dann wird dieser Junktor Sheffer-Operator oder Shefferfunktion (nach Henry Maurice Sheffer) genannt. Für die klassische Aussagenlogik gibt es genau zwei Sheffer-Operatoren: den Shefferstrich, auch NAND genannt {
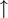 }, und den Peirce-Operator, auch NOR genannt {
}, und den Peirce-Operator, auch NOR genannt {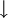 }.
}.Die Frage, welche der theoretisch möglichen Junktoren man für ein logisches System verwenden soll, ist – natürlich über die Anforderung funktionaler Vollständigkeit hinaus – rein pragmatischer Natur. In der klassischen Aussagenlogik (vgl. klassische Logik) sind die folgenden Junktoren am gebräuchlichsten (bezogen auf zwei Aussagen A und B):
- die Negation
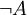 entspricht einer Verneinung
entspricht einer Verneinung - die materiale Implikation, auch Subjunktion oder Konditional genannt,
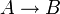 , entspricht der hinreichenden Bedingung „(Schon) wenn A, dann B“
, entspricht der hinreichenden Bedingung „(Schon) wenn A, dann B“ - das Bikonditional, auch Bisubjunktion oder Äquivalenz genannt,
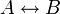 , entspricht einer hinreichenden und notwendigen Bedingung, „B genau dann, wenn A“
, entspricht einer hinreichenden und notwendigen Bedingung, „B genau dann, wenn A“ - die Konjunktion
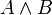 , das logische Und: „Sowohl A als auch B“
, das logische Und: „Sowohl A als auch B“ - die Disjunktion
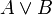 , das einschließende Oder: „Entweder A oder B oder beide“
, das einschließende Oder: „Entweder A oder B oder beide“
Intensionale Junktoren
Junktoren, bei denen der Wahrheitswert eines aus ihnen gebildeten Satzes nicht eindeutig von den Wahrheitswerten ihrer Teilsätze bestimmt ist, heißen intensionale Junktoren. Intensional sind z. B. die einstelligen Modaloperatoren „es ist notwendig, dass“ und „es ist möglich, dass“ (siehe Modallogik): Dass eine Aussage wahr ist, bedeutet intuitiv noch nicht, dass diese Aussage auch notwendig ist; und dass eine Aussage falsch ist, bedeutet noch nicht, dass sie unmöglich ist. Wahrheitsfunktional lässt sich den Modalitäten daher wohl nicht beikommen.
Ein anderes Beispiel ist die intuitionistische Logik, in der die in der klassischen Logik vorkommenden Konnektive auf andere Weise und nicht wahrheitsfunktional interpretiert werden.
Zur Interpretation intensionaler Junktoren benötigt man komplexere Mechanismen als die extensionalen Wahrheitstabellen. Die erste bedeutende formale Semantik intensionaler Junktoren ist wohl die von Saul Aaron Kripke ursprünglich zur Interpretation der Modallogik entwickelte Kripke-Semantik (siehe Modallogik). Kripke-Semantik eignet sich auch zur Interpretation intuitionistischer Logik.
Siehe auch: Philosophische Logik in Logik.
Beispiele
- Wahrheitstafel für den Konjunktor in der zweiwertigen klassischen Logik
A B 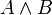
wahr wahr wahr wahr falsch falsch falsch wahr falsch falsch falsch falsch - Wahrheitstafel für den Disjunktor in der zweiwertigen klassischen Logik
A B 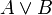
wahr wahr wahr wahr falsch wahr falsch wahr wahr falsch falsch falsch - Wahrheitstafel für die materiale Implikation in der zweiwertigen klassischen Logik
A B 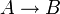
wahr wahr wahr wahr falsch falsch falsch wahr wahr falsch falsch wahr - Wahrheitstafel für den Konjunktor in der dreiwertigen Logik Ł3 von Jan Łukasiewicz (1920)
A B 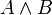
1 1 1 1 0,5 0,5 1 0 0 0,5 1 0,5 0,5 0,5 0,5 0,5 0 0 0 1 0 0 0,5 0 0 0 0 - Wahrheitstafel für den Konjunktor in der dreiwertigen Logik B3 von Dimitri Analtoljewitsch Bočvar (1938)
A B 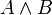
1 1 1 1 0,5 0,5 1 0 0 0,5 1 0,5 0,5 0,5 0,5 0,5 0 0,5 0 1 0 0 0,5 0,5 0 0 0 In der Dialogischen Logik: Opponent Proponent 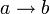
a? (Die Subjunktionsbehauptung wird angegriffen nach der Subjunktionsregel: Die voranstehende Pa wird behauptet.) b (Als Verteidigung wird das nachstehende b genannt, dies kann durch eine Übernahme des a der vorigen Zeile verteidigt werden. Es kann – je nach Regelsatz – auch erst die Aussage a angegriffen werden.) -
Wikimedia Foundation.
