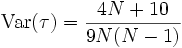Rangkorrelation nach Spearman

Ein Rangkorrelationskoeffizient ist ein parameterfreies Maß für Korrelationen, das heißt, er misst, wie gut eine beliebige monotone Funktion den Zusammenhang zwischen zwei Variablen beschreiben kann, ohne irgendwelche Annahmen über die Wahrscheinlichkeitsverteilung der Variablen zu machen.

Anders als Pearsons Korrelationskoeffizient, benötigt er weder die Annahme, dass die Beziehung zwischen den Variablen linear ist, noch ist es erforderlich, dass die Variablen auf einer Intervallskala gemessen werden. Er kann für Variablen benutzt werden, die auf Ordinalskalenniveau gemessen werden.

Der Rangkorrelationskoeffizient ist robust gegenüber Ausreißern und ist auch für nichtlineare Zusammenhänge verwendbar.

Es gibt zwei bekannte Rangkorrelationskoeffizienten: Spearmans Rangkorrelationskoeffizient und Kendalls Tau. Während Spearmans Rho von einer Gleichabständigkeit (= Äquidistanz) der Skalenwerte/Ränge ausgeht, basiert Tau rein auf ordinaler Information. Das ist z. B. bei den oft genutzten Likert-Skalen von Bedeutung . Zur Ermittlung der Übereinstimmung zwischen mehreren Beobachtern (Interrater-Reliabilität) auf Ordinalskalenniveau wird dagegen auf den mit den Rangkorrelationskoeffizienten verwandten Konkordanzkoeffizient W nach Kendall zurückgegriffen.

Konzept

Wir beginnen mit N Paaren von Messungen (x_i,y_i). Das Konzept der nichtparametrischen Korrelation besteht darin, den Wert x_i einer jeden Messung durch den Rang relativ zu allen anderen x_j in der Messung zu ersetzen, also 1,2,3,...,N. Nach dieser Operation stammen die Werte von einer wohlbekannten Verteilung, nämlich einer Gleichverteilung von Zahlen zwischen 1 bis N. Falls die x_i alle unterschiedlich sind, kommt jede Zahl genau einmal vor. Falls manche x_i identische Werte haben, wird ihnen der Mittelwert der Ränge zugewiesen, die sie erhalten hätten, wenn sie leicht unterschiedlich gewesen wären. Dieser gemittelte Rang ist manchmal eine ganze Zahl, manchmal ein „halber“ Rang. In allen Fällen ist die Summe aller zugewiesener Ränge gleich der Summe aller Zahlen von 1 bis N, nämlich N(N + 1) / 2.

Anschließend wird genau dieselbe Prozedur mit den y_i durchgeführt und jeder Wert durch seinen Rang unter allen y_j ersetzt.

Durch das Ersetzen der Originalwerte in Ränge geht Information verloren. Die Anwendung bei intervallskalierten Daten kann aber dennoch sinnvoll sein, da eine nichtparametrische Korrelation robuster ist als die lineare Korrelation, widerstandsfähiger gegen ungeplante Fehler und Ausreißerwerte in den Daten, genau wie der Median robuster ist als der Mittelwert. Liegen als Daten nur Rangreihen, also Daten auf Ordinalniveau vor, gibt es zudem keine Alternative zu Rangkorrelationen.

Spearmans Rangkorrelationskoeffizient

Spearmans Rangkorrelationskoeffizient ist benannt nach Charles Spearman und wird oft mit dem griechischen Buchstaben ρ (rho) oder – in Abgrenzung zum Pearson’schen Produkt-Moment-Korrelationskoeffizienten als r_s bezeichnet.

Im Prinzip ist ρ ein Spezialfall des Pearsons Produkt-Moment Korrelationskoeffizienten, bei dem die Daten in Ränge konvertiert werden, bevor der Korrelationskoeffizient berechnet wird:

$r_s = \frac{\sum_{i}(rg(x_i)-\overline{rg}_x)(rg(y_i)-\overline{rg}_y)} {\sqrt{\sum_{i}(rg(x_i)-\overline{rg}_x) ^2}\sqrt{\sum_{i}(rg(y_i)-\overline{rg}_y)^2}}$.

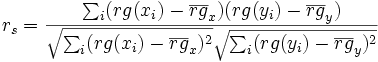mit:

rg(x) = Rang von x

In der Praxis wird meistens eine einfachere Formel zur Berechnung von ρ benutzt.

Die Rohdaten werden in Ränge konvertiert und die Differenz d_i zwischen den Rängen beider Variablen werden für jede Beobachtung berechnet. ρ ist dann gegeben durch:

$r_s = 1 - \frac{6 \sum_{i} d_i^2} { n \cdot (n^2 - 1)} \qquad \text{mit} \quad d_i = rg(x_i)-rg(y_i)$,

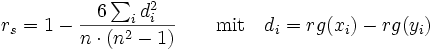mit:

d = die Differenz zwischen den Rängen von x und y einer Beobachtung und

n = Anzahl der Wertepaare.

Sind alle Ränge verschieden, ergibt diese einfache Formel exakt dasselbe Ergebnis.

Die Formel wird etwas komplizierter, wenn identische Werte für X oder Y existieren, aber solange nicht sehr viele Werte identisch sind, ergeben sich nur kleine Abweichungen.

Beispiele

Beispiel 1

Als Beispiel sollen Größe und Körpergewicht verschiedener Menschen untersucht werden. Die Paare von Messwerten seien 175 cm, 178 cm und 190 cm und 65 kg, 70 kg und 98 kg.

In diesem Beispiel besteht die maximale Rangkorrelation: Die Datenreihe der Körpergröße wird nach Rang geordnet, und die Rangzahlen der Körpergrößen entspricht auch den Rangzahlen der Körpergewichte. Eine niedrige Rangkorrelation herrscht, wenn etwa die Körpergröße im Verlauf der Datenreihe größer wird, das Gewicht jedoch abnimmt. Dann kann man nicht „Der schwerste Mensch ist der größte“ sagen. Der Rangkorrelationskoeffizient ist der zahlenmäßige Ausdruck des Zusammenhanges zweier Rangordnungen.

Beispiel 2

Es seien zwei Datenreihen a und b mit den folgenden Werten:

Werte von a	Werte von b	Rang von a	Rang von b	Differenz zwischen den Rängen	Quadrat der Differenz
2	1.5	1	2.5	−1.5	2.25
3	1.5	2.5	2.5	0	0
3	4	2.5	5	−2.5	6.25
5	3	4	4	0	0
5.5	1	5	1	4	16
8	5	6	6.5	−0.5	0.25
10	5	7.5	6.5	1	1
10	9.5	7.5	8	−0.5	0.25
				Summe der Quadrate -->	26

Die Tabelle ist nach der Reihe a geordnet. Wichtig ist, dass sich Einzelwerte einen Rang teilen können. In der Reihe a gibt es zwei „3“, und sie haben jeweils den „durchschnittlichen“ Rang (2+3)/2 = 2.5. Dasselbe geschieht bei der Reihe b. Die Signifikanz wird durch den Vergleich von Ergebnis mit Tabellenwert festgestellt.

Je höher die Summe der Rangdifferenzquadrate, desto tiefer ist die Rangkorrelation nach Spearman.

Bestimmung der Signifikanz

Der moderne Ansatz für den Test, ob der beobachtete Wert von ρ sich signifikant von null unterscheidet führt zu einem Permutationstest. Dabei wird die Wahrscheinlichkeit berechnet, dass ρ für die Nullhypothese größer oder gleich dem beobachteten ρ ist.

Dieser Ansatz ist traditionellen Methoden überlegen, wenn der Datensatz nicht zu groß ist, um alle notwendigen Permutationen zu erzeugen, und weiterhin, wenn nicht klar ist, wie man für die gegebene Anwendung sinnvolle Permutationen für die Null-Hypothese erzeugt (was aber normalerweise recht einfach ist).

Kendalls Tau

Kendalls τ ist sogar noch weniger parametrisch als Spearmans ρ. Anstelle der numerischen Differenz der Ränge nutzt es nur die relative Anordnung der Ränge: Höherer Rang, niedrigerer Rang, gleicher Rang. In diesem Fall müssen die Daten nicht einmal in Ränge umgerechnet werden; Äquidistanz zwischen den Skalenwerten wird hier nicht unterstellt: Die Ränge sind höher, niedriger oder gleich, genau wenn jeweils die Werte größer, kleiner oder gleich sind. Oft wird ρ als direkterer nichtparametrischer Test vorgezogen, beide Statistiken sind aber weit verbreitet. Tatsächlich sind ρ und τ sehr stark korreliert und zeigen in den meisten Anwendungen tatsächlich dieselbe Wirkung.

Speziell empfohlen wird τ, wenn die Daten nicht normal verteilt sind, die Skalen ungleiche Teilungen aufweisen oder bei sehr kleinen Stichprobengrößen.

Berechnung

Um τ zu berechnen beginnen wir mit N Datenpunkten (x_i,y_i). Nun betrachten wir alle 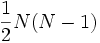$\frac{1}{2} N (N-1)$ Paare von Datenpunkten in denen nur verschiedene Datenpunkte enthalten sind und beide Anordnungen als verschiedene Paare zählen.

Wir nennen ein Paar übereinstimmend, wenn die Anordnung der relativen Größen der beiden x mit der Anordnung der relativen Größen der beiden y übereinstimmt.

Wir nennen ein Paar uneinig, wenn die x andersherum angeordnet sind als die beiden y.

Falls die beiden x gleich sind, wird das Paar extra_y genannt. Falls die beiden y gleich sind, wird das Paar extra_x genannt. Falls die beiden x gleich sind und die beiden y gleich sind, wird das Paar überhaupt nicht benannt.

Nachdem ausgezählt ist, wieviele Paare es von jeder Sorte gibt, kann man Kendalls τ wie folgt berechnen:

$\tau = \frac{uebereinstimmend-uneinig}{\sqrt{uebereinstimmend+uneinig+extra_y} \sqrt{uebereinstimmend+uneinig+extra_x }}$

Es ist leicht zu sehen, dass dieser Wert immer zwischen +1 und −1 liegt und die Extremwerte nur für perfekte Übereinstimmung der Ränge und perfekte Umkehrung der Ränge annimmt.

Varianz

Kendall hat über kombinatorische Überlegungen herausgefunden, dass τ unter der Null-Hypothese (kein Zusammenhang zwischen x und y) annähernd normalverteilt ist. Dabei ist der Mittelwert 0 und die Varianz:

$\mathrm{Var}(\tau) = \frac{4N+10}{9N(N-1)}$