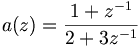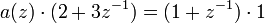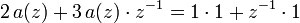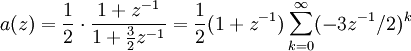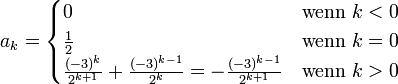Rekursionsgleichung

In der Mathematik wird durch eine Differenzengleichung (DzGl) (auch als Rekursionsgleichung bezeichnet) eine Folge rekursiv definiert. Das heißt, dass jedes Folgenglied eine Funktion der vorhergehenden Folgenglieder ist:

x_n = f(x_{n − 1},x_{n − 2},...,x₁,x₀)

für natürliche Zahlen n. Eine Spezialform sind die linearen Differenzengleichungen.

Herkunft und Anwendung

In der Ingenieurwissenschaft ist die Differenzengleichung eine Rechenvorschrift zur Berechnung einer Ausgangsfolge respektive eines Ausgangssignals. Im Sinne der Zeitreihenanalyse lässt sich eine Differenzengleichung auch allgemeiner als Gleichung definieren, mit der sich die Werte einer Zeitreihe berechnen lassen, die rekursiv zusammenhängen.

Nach der Diskretisierung eines kontinuierlichen Signals kann aus der Folge keine Ableitung mehr berechnet werden, man muss sich hier des Differenzenquotienten bedienen. Eine Differenzengleichung ist das zeitdiskrete Pendant zur Differentialgleichung und findet ihre Anwendung vor allem in der digitalen Signalverarbeitung (z. B. im Zusammenhang mit dem Entwurf von Filtern).

Anwendungsbeispiele aus der Zeitreihenanalyse sind die Tilgungsrate eines Annuitäten-Kredits (deterministischer Zusammenhang) oder der Bestand an Arbeitslosen (stochastischer Zusammenhang).

Zusammenhang Differenzengleichung und z-Transformation

Die z-Transformation nimmt die gleiche Stellung für zeitdiskrete Signale (Folgen) ein, wie die Laplacetransformation für den kontinuierlichen Zeitbereich.

Vom Zeitdiskreten in den z-Bildbereich

Vom z-Bildbereich zum Zeitdiskreten

Es gibt hier viele Möglichkeiten: Durch Tabellen, Taylorreihenentwicklung, nichtabbrechende Division u. a. Ein weiteres Hilfsmittel ist

Die Übertragungsfunktion

Ausdrücke in z können sehr einfach mit Hilfe einer Übertragungsfunktion der Variablen und eines Stoßes (im Diskreten) in eine Differenzengleichung übersetzt werden.

Betrachtet man beispielsweise die Funktion

$a(z)=\frac{1 + z^{-1}}{2 + 3z^{-1}}$

dann erhält man als Beziehung zwischen a(z) und 1

$a(z) \cdot ( 2 + 3z^{-1}) = ( 1 + z^{-1} )\cdot 1$

Multipliziert man diese Gleichung aus zu

$2\,a(z) + 3\,a(z) \cdot z^{-1} = 1 \cdot 1 + z^{-1} \cdot 1$

so erhält man mit Hilfe des Verschiebungssatzes

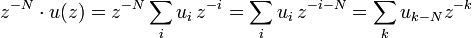$z^{-N} \cdot u(z)=z^{-N}\sum_i u_i\,z^{-i}=\sum_i u_i\,z^{-i-N}=\sum_k u_{k-N}z^{-k}$ (dabei ist k=i+N)

durch Koeffizientenvergleich im betrachteten Beispiel

$2\,a_k + 3\,a_{k-1} = \delta_{0,k} + \delta_{0,k-1}$.

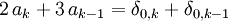Eine Lösung dieser Differenzengleichung kann mittels der geometrischen Reihe bestimmt werden, dazu wird der Nenner von a(z) durch Erweitern auf die Form 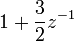$1+\frac32z^{-1}$ gebracht:

$a(z)=\frac12\cdot\frac{1+z^{-1}}{1+\frac32z^{-1}}=\frac12(1+z^{-1})\sum_{k=0}^\infty (-3z^{-1}/2)^k$

woraus sich

$a_k = \begin{cases} 0 & \mbox{wenn }k<0\\ \frac{1}{2} & \mbox{wenn }k=0\\ \frac{(-3)^k}{2^{k+1}}+\frac{(-3)^{k-1}}{2^k}=-\frac{(-3)^{k-1}}{2^{k+1}} & \mbox{wenn }k>0 \end{cases}$

ergibt.

Dies ist eine Anwendung der Methode der erzeugenden Funktionen.

Anmerkung: Der diskrete Deltastoß bzw. das Kronecker-Delta δ(k) = δ_0,k hat immer den Wert 0, außer bei k=0, wo er den Wert 1 annimmt.

Differenzengleichungen in der Ökonomie

In der ökonomischen Theorie kommen Differenzengleichungen vor allem zum Einsatz, um die Entwicklung ökonomischer Größen über die Zeit zu analysieren. Vor allem Konjunktur und Wachstum werden vielmals in Form von Differenzengleichungen abgebildet. Man geht dabei davon aus, dass z. B. das Bruttoinlandsprodukt sich auf einem bestimmten Pfad hin zu einem langfristigen Gleichgewicht entwickelt in dem alle Kapazitäten ausgelastet sind. Je nach Lösung der Differenzengleichung ergibt sich der Entwicklungspfad als asymptotischer Verlauf oder als schwingender Verlauf (in etwa Kosinus-Kurven).

Siehe auch

• Rekursion
• Lineare Differenzengleichung
• Erzeugende Funktion

Literatur

• Berg, L.: Differenzengleichungen zweiter Ordnung mit Anwendungen, Darmstadt: Steinkopff, 1980.