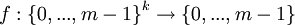- Rekursiver arithmetischer Zufallszahlengenerator
-
Arithmetische Zufallszahlengeneratoren sind Zufallszahlengeneratoren zur Erzeugung von Zufallszahlen, die auf der Arithmetik beruhen. Sie basieren auf dem Satz von Weyl, verwenden also
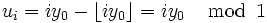
als Generator, wobei die Definitionen bei Satz von Weyl gelten, also insbesondere
![y_0 \in ]0, 1[](/pictures/dewiki/50/2f20424852ce0fb816c764ea0cfcf673.png) eine irrationale Zahl ist. Hierbei steht
eine irrationale Zahl ist. Hierbei steht 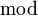 für die Modulo-Operation.
für die Modulo-Operation. 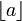 bezeichnet die größte Ganzzahl die kleiner oder gleich a ist.
bezeichnet die größte Ganzzahl die kleiner oder gleich a ist.Arithmetische Zufallszahlengenerator werden in der Praxis statt physikalischer Zufallszahlengeneratoren eingesetzt. Da auf Taschenrechnern oder Computern keine irrationalen Zahlen darstellbar sind, beschränkt man sich häufig auf rekursive arithmetische Zufallszahlengeneratoren.
Rekursive arithmetische Zufallszahlengeneratoren
Dies sind Zufallszahlengeneratoren, die auf arithmetischen Zufallszahlengeneratoren basieren, bei denen man sich jedoch mit bestimmten rationalen Zahlen als Zufallszahlen zufrieden gibt, da irrationale Zahlen, von denen arithmetische Zufallszahlengeneratoren ausgehen, auf Rechnern nicht darstellbar sind. Es handelt sich also um Pseudozufallszahlengeneratoren.
Zur Initialisierung des Generators verwendet man Startwerte
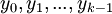 , die als Saat bezeichnet werden. Sie können z. B. fest vorgegeben werden, wenn die erzeugte Zahlenfolge wiederholbar sein soll, oder man initialisiert sie auf zufällige Weise. Häufig verwendet man dafür die Rechneruhr als Datenquelle, die aktuelle Uhrzeit bestimmt also die Initialwerte der
, die als Saat bezeichnet werden. Sie können z. B. fest vorgegeben werden, wenn die erzeugte Zahlenfolge wiederholbar sein soll, oder man initialisiert sie auf zufällige Weise. Häufig verwendet man dafür die Rechneruhr als Datenquelle, die aktuelle Uhrzeit bestimmt also die Initialwerte der 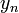 .
.Eine arithmetische Funktion
erzeugt nun sukzessive die Werte
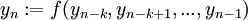 , wobei
, wobei 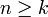 .
.
Als Zufallszahlen im Intervall [0;1[ verwendet man dann z. B.:
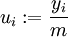 .
.
Man gibt sich für die Zufallszahlen also mit Werten aus der Menge
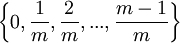 zufrieden, wobei m eine hinreichend große natürliche Zahl ist.
zufrieden, wobei m eine hinreichend große natürliche Zahl ist.Die wohl bedeutendsten rekursiven arithmetischen Zufallszahlengeneratoren sind Kongruenzgeneratoren.
Vorteile
Bei geeigneter Funktion f lassen sich schnell Zufallszahlen erzeugen. Diese sind bei Angabe der Saat vollständig reproduzierbar.
Nachteile
Die Folge
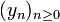 ist deterministisch. Es werden keine echten Zufallszahlen, sondern vielmehr nur Pseudozufallszahlen erzeugt. Es handelt sich also um einen Pseudozufallszahlengenerator. Die Determiniertheit bedingt auch, dass eine Unabhängigkeit und Gleichverteilung der Folge nicht gegeben ist. Insbesondere wird irgendwann eine Schleife erzeugt. Es gibt also
ist deterministisch. Es werden keine echten Zufallszahlen, sondern vielmehr nur Pseudozufallszahlen erzeugt. Es handelt sich also um einen Pseudozufallszahlengenerator. Die Determiniertheit bedingt auch, dass eine Unabhängigkeit und Gleichverteilung der Folge nicht gegeben ist. Insbesondere wird irgendwann eine Schleife erzeugt. Es gibt also 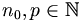 mit
mit 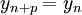 für alle
für alle 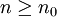 . Das kleinste p bezeichnet man hierbei als Periode.
. Das kleinste p bezeichnet man hierbei als Periode.Ob diese Nachteile aber eine Rolle spielen hängt von der Anwendung ab: Zum Beispiel ist es für Simulationen kein Nachteil, dass die generierten Zahlen vorhersagbar sind solange die Periodenlänge hinreichend groß ist. Im Gegenteil: Die Reproduzierbarkeit der Zahlen erleichtert die Analyse und Fehlersuche.
Arithmetische ZufallszahlengeneratorenKongruenzgenerator (linearer, multiplikativer, gemischt linearer, Fibonacci-Generator) | Inverser Kongruenzgenerator | Blum-Blum-Shub-Generator | Mersenne-Twister
Wikimedia Foundation.