Zufallszahlgenerator

Zufallszahlengenerator fehlen folgende wichtige Informationen: Güte wird nur mangelhaft behandelt Überschneidung mit spezielleren Artikeln sind zu dürftig oder zu ausschweifend Hard- und Softwaretechnische Realisierung ist sehr dürftig Du kannst Wikipedia helfen, indem du sie recherchierst und einfügst.

Dieser Artikel oder Abschnitt ist nicht hinreichend mit Belegen (Literatur, Webseiten oder Einzelnachweisen) versehen. Die fraglichen Angaben werden daher möglicherweise demnächst gelöscht. Hilf Wikipedia, indem du die Angaben recherchierst und gute Belege einfügst. Bitte entferne erst danach diese Warnmarkierung.

Als Zufallszahlengenerator, gelegentlich auch zu Zufallsgenerator oder schlicht Generator verkürzt, bezeichnet man ein Verfahren, das eine Folge von Zufallszahlen erzeugt. Der Bereich, aus dem die Zufallszahlen erzeugt werden, hängt dabei vom speziellen Zufallszahlengenerator ab. Es kann beispielsweise die Menge aller 32-Bit-Zahlen oder auch die Menge der reellen Zahlen im Intervall [0,1] sein. Meistens ist von einem Zufallszahlengenerator erwünscht, dass er gleichverteilte Werte aus dem jeweiligen Bereich erzeugt. Für gewisse statistische Simulationen sind auch solche Zufallszahlengeneratoren interessant, die eine vorgegebene Verteilung (z. B. Normalverteilung oder Poissonverteilung) erzeugen.

Zufallszahlen werden unter anderem bei verschiedenen Methoden der Statistik benötigt, z. B. bei der Auswahl einer Stichprobe aus einer Grundgesamtheit, bei der Verteilung von Versuchstieren auf verschiedene Versuchsgruppen (Randomisierung) oder bei der Monte-Carlo-Simulation. Typische weitere Anwendungsgebiete sind (Computer-, Glücks-) Spiele und diverse Kryptographieverfahren.

Man unterscheidet grundsätzlich zwischen nicht-deterministischen und deterministischen Zufallszahlengeneratoren. Nicht-deterministisch ist ein Zufallszahlengenerator dann, wenn er auch bei gleichen Ausgangsbedingungen unterschiedliche Werte liefert. Da die Implementierung einer Software-Prozedur immer deterministisch arbeitet, muss zur Realisierung eines nicht-deterministischen Zufallszahlengenerators ein externer, beispielsweise ein physikalischer, Vorgang einbezogen werden. Ein deterministischer Zufallszahlengenerator liefert bei gleichen Ausgangsbedingungen dagegen immer die gleiche Folge von Zahlen. Oft werden beide Formen zu einem hybriden Generator kombiniert.

Nichtdeterministische Zufallszahlengeneratoren

Physikalischer Zufallszahlengenerator

Ein physikalischer Zufallszahlengenerator dient zur Erzeugung von Zufallszahlen und benutzt dafür physikalische Prozesse.

Hierbei werden beispielsweise Impulsschwankungen elektronischer Schaltungen (z. B. thermisches Rauschen eines Widerstands oder radioaktive Zerfallsvorgänge) ausgenutzt.

Allerdings gelten physikalische Zufallszahlengeneratoren nicht als schnell, da eine Unabhängigkeit und Gleichverteilung der erzeugten Zufallszahlen nur durch hinreichend große Abstände bei der Beobachtung der physikalischen Prozesse bzw. Abfangverfahren erreicht werden können. Dies ist aber nur eine Frage der verwendeten Technik, denn Zufallsprozesse wie thermisches Rauschen haben Grenzfrequenzen von vielen Terahertz.

Auch ist eine Reproduzierbarkeit der Ergebnisse prinzipiell nicht möglich, da die produzierten Zufallszahlen echt zufällig sind, so wie die Ziehung der Lottozahlen. Dadurch sind die produzierten Zufallszahlen aperiodisch, d. h. die Folge der Zufallszahlen ist unendlich.

In der Praxis verwendet man daher häufig arithmetische Zufallszahlengeneratoren, die eine Mischform sind. Sie berechnen Pseudozufallszahlen, verwenden dafür allerdings – bei Bedarf – einen echt zufälligen Startwert.

In der Praxis findet man solche hybriden Zufallszahlengeneratoren unter Linux/Unix/BSD unter /dev/random und /dev/urandom. Diese zeigen praktisch keinerlei statistische Auffälligkeiten.

Beispielsweise kann ein Geigerzähler die Zahl der radioaktiven Zerfälle in einer bestimmten Zeitspanne messen. Man nutzt die Tatsache, dass radioaktive Isotope nach einer rein zufälligen Zeitspanne in das Tochterelement bzw. -isotop zerfallen. Die Zeitspanne hat aber beim gleichen Isotop immer den gleichen Mittelwert (die sogenannte Halbwertszeit). Da der radioaktive Zerfall unabhängig von Umgebungsbedingungen abläuft, kann dieser Vorgang Zufallszahlen hoher Güte liefern.

Daneben können auch Rauschgeneratoren als Zufallsgeneratoren verwendet werden.^[1]

Eine weitere Methode zum Aufbau von Zufallsgeneratoren in digitalen Schaltungen besteht in der Ausnützung der Metastabilität bei taktflankengesteuerten Flipflops.^[2]

Bei physikalischen Zufallszahlengeneratoren gibt es allerdings das Problem der Alterung. Beispielsweise haben Geiger-Müller-Zählrohre eine Lebensdauer von typischerweise einer Billion Pulse und sind zudem abhängig von Temperatur, Magnetfeldern und der Versorgungsspannung. Zudem muss bei Geigerzählern die Pulsrate „deutlich höher“ als die Taktfrequenz sein, mit der die Pulse eingelesen werden. Eine Lösung dieses Problems ist viele mehr oder minder gute Zufallszahlengeneratoren zu nehmen und von diesen Zufallszahlen nur das letzte Bit zu verwenden um damit die Modulo-Zwei-Summe zu bilden. Nach dem zentralen Grenzwertsatz der Statistik erhält man damit auch mit schlechten Zufallszahlengeneratoren perfekt zufällige Zufallsbits, wenn man nur genügend viele Zufallszahlengeneratoren verwendet.

Quasizufällige Ereignisse

Es wird beispielsweise die Systemzeit bestimmt, in der eine Benutzeraktion eintritt. Auf diese Weise erzeugte Zufallszahlen haben meist eine geringe Güte, lassen sich aber als Startwert für deterministische Verfahren verwenden.

Deterministische Zufallszahlengeneratoren

Deterministische Zufallszahlengeneratoren erzeugen Pseudozufallszahlen und werden daher in der Regel Pseudozufallszahlengeneratoren genannt (engl. PRNG, pseudo random number generator). Sie erzeugen eine Zahlenfolge, die zwar zufällig aussieht, es aber nicht ist, da sie durch einen deterministischen Algorithmus berechnet wird. Bei jedem Start der Zufallszahlenberechnung mit gleichem Startwert, der so genannten Saat (engl. seed), wird die gleiche pseudozufällige Zahlenfolge erzeugt.

Sie verletzen damit Eigenschaften echter Zufallszahlen, sind jedoch von Computern wesentlich einfacher zu erzeugen.

Sie sind in praktisch allen Programmiersprachen verfügbar. Dass es sich bei diesen Implementationen lediglich um Generatoren handelt, die pseudozufällige Zahlen (von oftmals nur geringer Güte) erzeugen, wird häufig übersehen.

Des weiteren vorteilhaft ist, dass diese deterministisch erzeugten Pseudozufallszahlen bei hinreichend genauer Dokumentation später reproduziert werden können. Diese Eigenschaft der Reproduzierbarkeit ist bedeutsam für die Anerkennung wissenschaftlicher Experimente.

Güte eines Pseudozufallszahlengenerators

Die erzeugten Zahlen werden durch statistische Eigenschaften charakterisiert. Dazu gehört die erzeugte Verteilung (z. B. Normalverteilung, Gleichverteilung, Exponentialverteilung etc.) oder die Unabhängigkeit aufeinanderfolgender Zahlen. Wie gut die erzeugten Zahlen den statistischen Vorgaben entsprechen, bestimmt die Güte eines Pseudozufallszahlengenerators.

Besonders strenge Anforderungen werden an kryptographisch sichere Zufallszahlengeneratoren gestellt.

Am Beispiel eines Pseudozufallszahlengenerators, der nur die Zahlen 0 und 1 ausgeben kann (z. B. simulierter Münzwurf), kann man sich klar machen, dass allein die gleiche Häufigkeit beider Ergebnisse nicht ausreicht, da etwa die Folge 0, 1, 0, 1, 0, 1, 0, 1, ... intuitiv nicht zufällig erscheint. Es sollten möglichst auch die möglichen Paare aufeinander folgender Ergebnisse mit den erwarteten Häufigkeiten auftreten, ja möglichst auch Tripel, Quadrupel usw. Diese Überlegungen führen auf den Spektraltest.

Ein sehr einfaches Gütekriterium ist die Periodenlänge, die im Verhältnis zum Wertebereich möglichst lang sein sollte. Dies ist etwa beim Mersenne-Twister in besonders starkem Maße der Fall. Ein simpler linearer Kongruenzgenerator kann dagegen den Wertebereich pro Periode bestenfalls einmal durchlaufen; dies sollte umgekehrt als Mindestanforderung gesehen werden und kann durch ein einfaches Kriterium geprüft werden (Satz von Knuth).

Weitere Gütetests beruhen auf dem Chi-Quadrat-Test, dem Kolmogorow-Smirnow-Test u. a.

Knuth listet noch zahlreiche andere Tests, so den serial test, den Lücken-Test, den Poker-test, den Couponsammler-Test, den Permutations-Test, den Lauf-Test, den Maximum-aus-t-Test und den Kollisions-Test. Es geschieht durchaus, dass ein Generator bei mehreren Tests sehr gut abschneidet, aber bei einem anderen versagt. Für einige Anwendungen, etwa Simulationen, die den entsprechenden Testbedingungen nahe sind, ist solch ein Generator dann ungeeignet.^[3]

Nicht-periodischer/unendlicher Generator

Man nehme die Nachkommastellen einer Wurzel einer ganzen Zahl als Zufallszahlen. Hierbei ist selbstverständlich darauf zu achten, dass die resultierende Wurzel eine irrationale Zahl ist, das heißt, dass 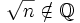$\sqrt{n}\notin \mathbb{Q}$ gilt, was immer der Fall ist, wenn die Wurzel keine ganze Zahl ist. Klassischerweise kann man statt 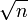$\sqrt{n}$ auch die Kreiszahl Pi verwenden. Zwar ist hierbei garantiert, dass die erzeugte Zahlenfolge nicht periodisch ist, jedoch ist bei diesen Beispielen noch nicht einmal bekannt, ob sie gleichverteilt ist, von weiter gehenden statistischen Tests ganz zu schweigen (siehe Normale Zahl). Aufgrund der endlichen Speicherkapazität eines Computers kann es in der Praxis jedoch keinen nicht-periodischen deterministischen Zufallszahlengenerator geben. Möglich sind aber nicht-periodische deterministische Zufallszahlengeneratoren mit zwei Takt-Generatoren, deren Takte inkommensurabel sind; wenn also deren Frequenzverhältnis 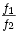$\tfrac{f_1}{f_2}$ eine irrationale Zahl ist, also n₁ * f₁ = n₂ * f₂ nicht erfüllt wird. Weil unter den reellen Zahlen die rationalen Zahlen eine Lebesgue-Nullmenge bilden, ist dies praktisch immer der Fall und damit ein aus beiden Takten generiertes Signal nichtperiodisch. Ein Beispiel hierfür ist ein mit der Frequenz f₁ erzeugtes Pseudozufallssignal, das mit der Frequenz f₂ abgetastet/eingelesen wird.

Softwaretechnische Realisierungen

• Arithmetische Zufallszahlengeneratoren basieren auf der Arithmetik. Irrationale Zahlen wie 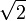$\sqrt{2}$ oder e können als Zufallszahlengeneratoren verwendet werden, indem man den gebrochenen Teil beliebiger Vielfache als Zufallszahlen nutzt. Nachteil des Verfahrens ist, dass sich irrationale Zahlen nur als Näherungswerte innerhalb der Rechengenauigkeit darstellen lassen.
• Rekursiver arithmetischer Zufallszahlengenerator: Diese Verfahren beruhen auf der Berechnung einer neuen Zufallszahl aus einer oder mehreren vorhergehenden Zahlen. Die neu erzeugte Zahl wird gespeichert und geht bei erneutem Aufruf des Zufallszahlengenerators in die Berechnung ein. Beim allerersten Aufruf des Zufallszahlengenerators muss ein willkürlich gewählter Startwert, die Saat (meist engl.: seed) verwendet werden.
  • Kongruenzgenerator
    • linearer Kongruenzgenerator
      • multiplikativer Kongruenzgenerator
      • gemischter linearer Kongruenzgenerator
    • Fibonacci-Generator
  • Inverser Kongruenzgenerator
  • Mersenne-Twister

Hardwaretechnische Realisierungen

• Schieberegister mit Rückkopplung
  • lineares Schieberegister
  • nichtlineares Schieberegister

Hardwaretechnische Komponenten

• Komplizierte Variante: Einbau einer radioaktiven Quelle deren Strahlung gemessen wird und als Basis des Zufallszahlengenerators dient.
• Einfacher ist die Realisierung mittels Rauschgenerators.

Hybride Generatoren

Pseudozufallszahlengeneratoren, die als Input einige wenige echte Zufallszahlen verwenden, also nicht nur Pseudozufallszahlen erzeugen. Ein Beispiel hierfür ist /dev/urandom unter Linux u. A.. Im einfachsten Fall wird einfach ein Pseudozufallszahlengenerator genommen, der gelegentlich mit einer neuen echten Zufallszahl als Startwert neu gestartet wird.

Sonstige Zufallszahlengeneratoren

• Auszählreime in Kinderspielen stellen eine Art deterministischer Zufallszahlengeneratoren dar.
• Das Mischen bei einem Kartenspiel ist ein nicht-deterministischer Zufallszahlengenerator.
• Eigentlich physikalische Verfahren zur Generierung von Zufallszahlen sind auch Würfeln und der Prozess der Ziehung von Lottozahlen mit den dafür typischen Maschinen. (Siehe Auch: Ziehung der Lottozahlen)

Siehe auch

• Kryptographisch sicherer Zufallszahlengenerator

Einzelnachweise

1. ↑ W. Baier (Hrsg.): Elektronik Lexikon. 2. Auflage. Franckh'sche Verlagshandlung, Stuttgart 1982, S. 485.
2. ↑ D. J. Kinniment et al.: Design of an on–chip random number generator using metastability. In: Proceedings of the 28th European Solid-State Circuits Conference, 24.–26. September 2002, S. 595–598.
3. ↑ D. E. Knuth, The Art of Computer Programming, Volume 2: Seminumerical Algorithms. Addison Wesley, Reading (MA) 1997, ISBN 0-201-89684-2.

Weblinks

• Beispielhafte Implementierung für einen AVR Mikocontroller (Assembler)
• Webbasierter Zufallszahlengenerator/English
• Echte (physikalische) Zufallszahlengeneratoren und deren Theorie
• Glossar zu Begriffen rund um echte Zufallszahlen
• Zufallsgenerator für eine randomisierte Verteilung in Gruppen (z.B. für Laborversuche)