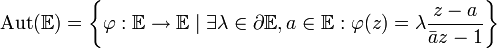Automorphismengruppe

In der Mathematik ist ein Automorphismus ein Isomorphismus einer Struktur auf sich selbst.

Definition

In einer beliebigen Kategorie ist ein Automorphismus eines Objekts A ein Homomorphismus 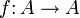$f\colon A \to A$ von A in sich selbst (also ein Endomorphismus), zu dem es einen inversen Homomorphismus gibt, also ein 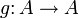$g\colon A\to A$ mit $g\circ f = f\circ g={\mathrm id}_A$.

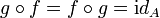Warnhinweis

In einer konkreten Kategorie, d.h. wenn die Objekte Mengen mit einer Zusatzstruktur und die Morphismen (spezielle) Abbildungen sind, ergibt sich, dass ein Automorphismus f als Abbildung zumindest bijektiv sein muss.

Zwar sind beispielsweise die Automorphismen eines Vektorraumes V genau die bijektiven linearen Abbildungen 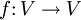$f\colon V \to V$, das Entsprechende gilt jedoch nicht notwendig für jede konkrete Kategorie, d.h. nicht jeder bijektive Endomorphismus ist notwendigerweise ein Automorphismus. 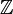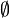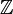Man betrachte etwa die Kategorie Top der topologischen Räume und hierin die Menge $\Z$ mit derjenigen Topologie, deren offene Mengen außer $\emptyset$ und $\Z$ beliebige Mengen positiver ganzer Zahlen sind – die Menge wird also je „zur Hälfte“ mit der Klumpen- bzw. der diskreten Topologie versehen. Dann ist 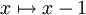$x\mapsto x-1$ eine stetige Bijektion, aber die Umkehrung 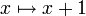$x\mapsto x+1$ ist nicht stetig (das Urbild von {1} ist die nicht offene Menge {0}).

Beispiele

Automorphismen von Gruppen

In der Gruppentheorie ist ein Automorphismus einer Gruppe G ein bijektiver Homomorphismus von G nach G.

Automorphismen sind zum Beispiel:

• in 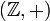$(\mathbb{Z}, +)$ die Negation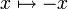 $x\mapsto -x$
• in 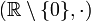$(\mathbb{R}\setminus\{0\}, \cdot)$ die Kehrwertbildung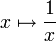 $x\mapsto\frac{1}{x}$
• in einer abelschen Gruppe 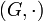$(G,\cdot)$ die Inversion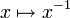 $x\mapsto x^{-1}$
• in 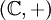$(\mathbb{C}, +)$ die komplexe Konjugation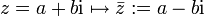 $z = a+b\mathrm{i} \mapsto \bar z := a-b\mathrm{i}$
• in einer Gruppe 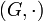$(G,\cdot)$ die Konjugation mit festem 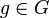$g\in G$, d.h.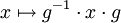 $x\mapsto g^{-1} \cdot x \cdot g$

Automorphismen von Graphen

In der Graphentheorie ist ein Automorphismus eines Graphen eine Permutation der Knoten, die den Graphen auf sich selbst abbildet (die permutierten Knoten sind durch dieselben Kanten verbunden wie die ursprünglichen).

Zum Beispiel geht dieser Graph

1 --- 2     3 --- 4

durch Vertauschen der Knoten-Identifikationsnummern 1 und 2 in diesen Graphen über

2 --- 1     3 --- 4

Diese Operation ist ein Automorphismus. Vertauscht man jedoch im ersten Graphen die Knoten-Identifikationsnummern 2 und 3, erhält man den Graphen

1 --- 3     2 --- 4

der nun andere Kanten als der erste hat. Daher ist diese Vertauschung kein Automorphismus.

Automorphismengruppe

Die Menge aller Automorphismen eines Objekts X zusammen mit der Komposition von Morphismen bildet eine Gruppe, die so genannte Automorphismengruppe von X, geschrieben als Aut(X). Einzusehen ist das ganz leicht:

• Abgeschlossenheit: Die Komposition zweier Isomorphismen ist ein Isomorphismus, und die Komposition zweier Endomorphismen ist ein Endomorphismus.
• Assoziativität ist bei der Komposition immer erfüllt.
• neutrales Element: Der identische Morphismus id_X ist ein Automorphismus.
• inverses Element: Das Inverse eines Automorphismus existiert per Definition von Isomorphismus und ist selbst wieder ein Isomorphismus und Endomorphismus, also ein Automorphismus.

Wenn es möglich ist, Elemente einer Struktur zu nehmen und mit ihnen Automorphismen zu bilden, dann unterscheidet man zwischen

• inneren Automorphismen
• äußeren Automorphismen

Für eine Gruppe G ist ein innerer Automorphismus ein Automorphismus f_g: G -> G der Form f_g(h) =g^-1hg (das ist die Konjugation mit g). Die inneren Automorphismen bilden einen Normalteiler von Aut(G), der mit Inn(G) bezeichnet wird.

Beispielsweise ist in der Funktionentheorie die Automorphismengruppe der Einheitskreisscheibe 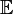$\mathbb{E}$ gegeben durch:

$\operatorname{Aut}(\mathbb{E}) = \left\{ \varphi:\mathbb{E}\to\mathbb{E} \mid \exists \lambda\in\partial\mathbb{E}, a\in\mathbb{E} : \varphi(z)=\lambda\frac{z-a}{\bar{a}z-1} \right\}$

Siehe auch

• Morphismus