Rittersches Schnittverfahren

Das Rittersche Schnittverfahren geht auf August Ritter (*1826, †1908) zurück. Es dient der Berechnung von Stabkräften in Fachwerken.

Damit ein System unter der Wirkung von gegebenen Kräften im Gleichgewicht ist, ist es notwendig und hinreichend, dass jedes Teilsystem sich in einem Gleichgewicht aus Zug- und Druckkräften sowie Drehmomenten befindet. Mit diesem so genannten Erstarrungsprinzip werden für ein aus mehreren Stäben bestehendes Fachwerk die Auflagerkräfte berechnet. Danach wird der Ritter-Schnitt angewandt:

Verfahrensprinzip

Das zweidimensionale Fachwerk wird in zwei Teile zerschnitten, und zwar genau so, dass maximal drei Stäbe freigelegt werden (von diesen müssen sich jeweils genau zwei in einem Punkt schneiden). Für diese Stäbe können die Kräfte nach den Gleichgewichtsbedingungen nun berechnet werden, da man drei linear unabhängige Gleichungen aufstellen kann.

$\sum M =0$,

$\sum F_y =0$,

$\sum F_x =0$

mit M = Moment, F_y = in y-Richtung, F_x = in x-Richtung wirkende Kräfte

Im dreidimensionalen Fachwerk können sechs Stabkräfte durch das Aufstellen eines linearen Gleichungssystems mit sechs linear unabhängigen Gleichungen berechnet werden.

Beispiel

Skizze

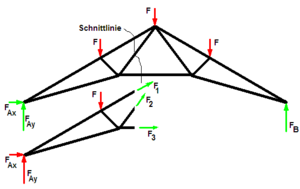
In diesem Beispiel werden die Stabkräfte bei einem Dachbinder ermittelt. Rote Kräfte sind gegeben, grüne Kräfte werden aus den Gleichgewichtsbedingungen ermittelt.

• Das Obere Bild zeigt den ganzen Binder mit Festlager links und Loslager rechts. (Die Kraft F_Bx ergibt sich zu Null.)
• Im Unteren Bild ist der Rittersche Schnitt dargestellt. Nach dem Schneiden können die drei Stabkräfte berechnet werden. Durch geschickte Wahl der Gleichgewichts-Gleichungen kann der Lösungsaufwand des linearen Gleichungssystems reduziert werden, beispielsweise durch

1. Summe der Momente um den Schnittpunkt der Stabkräfte F₂ und F₃ liefert direkt die Stabkraft F₁,
2. Summe der Vertikalkräfte (F_y) liefert direkt F₂,
3. Summe der Horizontalkräfte (F_x) liefert direkt F₃

Siehe auch

• Balkentheorie
• Cremonaplan

Literatur

• Ritter, August: Elementare Theorie und Berechnung eiserner Dach- und Brücken-Constructionen. Hannover: C. Rümpler, 1863.