- Fachwerk (Mechanik)
-
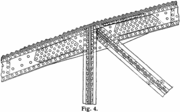
Fachwerk-Stahlbrücke über den Oulujoki in Finnland.
Historische Knotenpunktausführung mit vier angeschlossenen Stäben.
Fachwerke für Dächer und Brücken.
Fachwerke für Dächer und Hallen.
Räumliche Dachtragwerke.
Polonceaudachtragwerke.
Räumliches Tragwerk.
Ein Fachwerk ist eine Konstruktion aus mehreren Stäben, die an beiden Enden miteinander verbunden sind. Durch dieses Prinzip entstehen in den einzelnen Elementen nur Druck- und Zugkräfte, wodurch die hohe Tragfähigkeit von Fachwerkkonstruktionen entsteht.Inhaltsverzeichnis
Fachwerke im Bauwesen und Maschinenbau
Konstruktionen aus Fachwerken im Bauwesen und im Maschinenbau haben im Verhältnis zu ihrer Tragfähigkeit ein geringes Gewicht. Nachteilig ist ihre größere räumliche Ausdehnung im Gegensatz zu massiven Alternativen. Eine besondere Herausforderung stellt bei jeder Fachwerkkonstruktion die Ausbildung der Knotenpunkte dar, da dort meist große Kräfte zwischen den Stäben übertragen werden müssen.
Fachwerks-Konstruktionen finden im 21. Jahrhundert zum Beispiel Anwendung in
- Strommasten
- Bindern von großen Hallen
- Baustellenkräne
- Balkenbrücken
- Messeständen
- Deckenkonstruktionen
Fachwerke in der Mechanik
In der Mechanik sind Fachwerke Tragwerke, die aus gelenkig miteinander verbundenen Stäben bestehen. Die Untersuchung der Festigkeit und der Stabilität von Fachwerken ist ein Teilgebiet der Festigkeitslehre.
Ideale Fachwerke
Ein ideales Fachwerk ist gegeben, wenn in den Knoten keine Momente übertragen werden – solche Fachwerke verlieren ihre Eigenschaften auch dann nicht, wenn die Knoten als reibungsfreie Gelenke ausgeführt sind.
Kräfte werden im idealen Fachwerk nur längs der Stabrichtung übertragen; Lasten greifen nur in den Knoten an.
Diese Näherung ist in der Realität dadurch gegeben, dass die Stäbe (meistens deutlich länger als breit) kaum Momente aufnehmen können. Fehler entstehen dadurch, dass die Stäbe ein Eigengewicht haben und diese Last in den Knoten zu Momenten und in den Elementen zu einer Knickgefahr führt. Dem begegnet man mit Nullstäben, die lange, auf Druck beanspruchte und/oder waagerechte Stäbe stützen.
Brücken-Auflager sind unter anderem zur Vermeidung von durch die Durchbiegung verursachten Momenten als Rollengelenk ausgeführt.
Die Bedingung
- 2k = s + f
mit
- k: Anzahl der Knoten
- s: Anzahl der Stäbe
- f: Anzahl der zu bestimmenden Auflagerkräfte (Fesselungen)
für ein ebenes Fachwerk (zweidimensional) ist eine notwendige, aber keine hinreichende Bedingung für die statische Bestimmtheit eines Fachwerks. Statisch bestimmt ist ein Fachwerk genau dann, wenn sich alle in ihm auftretenden Stabkräfte berechnen lassen. Diese Bedingung ist erfüllt, wenn es sich um ein einfaches Fachwerk handelt: Bei diesem werden ausgehend von einem Stab jeweils zwei weitere Stäbe und ein Knoten hinzugefügt.
Im räumlichen, dreidimensionalen Fall lautet die Bedingung
- 3k = s + f.
Für die Berechnung der Stabkräfte im idealen Fachwerk gibt es verschiedene Rechenverfahren:
Knotenpunktverfahren (Rundschnittverfahren)
Mit dem Knotenpunktverfahren lassen sich die Stabkräfte durch Aufstellen eines Gleichungssystems ermitteln. Für jeden Knoten werden die zwei Gleichgewichtsbedingungen – die Summe der Kräfte in x- und in y-Richtung muss Null sein – aufgeschrieben. Dadurch ergibt sich ein Gleichungssystem, das bei statischer Bestimmtheit des Fachwerks gelöst werden kann.
Im dreidimensionalen Fall werden jeweils drei Gleichungen aufgestellt.
Bei einfachen Fachwerken genügt es, die Auflagerkräfte mit dem Erstarrungsprinzip zu berechnen und sich dann entlang der Knoten ‚durchzuhangeln‘.
Rittersches Schnittverfahren
Das Rittersche Schnittverfahren dient zur direkten Berechnung von Stabkräften im Fachwerk. Somit können immer drei Stabkräfte im zweidimensionalen oder sechs Stabkräfte im dreidimensionalen Fachwerk berechnet werden, ohne die anderen zu kennen oder gar vorher berechnen zu müssen.
Stabtauschverfahren
Das Hennebergsche Stabtauschverfahren wird bei nicht einfachen Fachwerken angewandt.
Cremonaplan
Der Cremonaplan dient bei statisch bestimmten Fachwerken der zeichnerischen Bestimmung der Stabkräfte zur Bemessung der Stäbe.
Nicht ideale Fachwerke
Reale Fachwerke sind außer der Reibung auch dem Auftreten von Biegungen unterworfen. Die Verformungs– und Spannungsberechnungen werden heutzutage im Allgemeinen mit der Finite-Elemente-Methode durchgeführt. Eine weitere Berechnungsmöglichkeit ist durch den Einsatz von Fließgelenken gegeben.
Siehe auch
Weblinks
Wikimedia Foundation.
