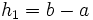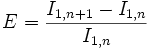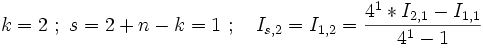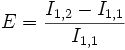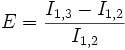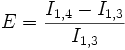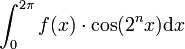- Rombergverfahren
-
Die Romberg-Integration ist ein Verfahren zur numerischen Bestimmung von Integralen und wurde von Werner Romberg entwickelt. Sie ist eine Verbesserung der (Sehnen)-Trapezregel durch Extrapolation.
Inhaltsverzeichnis
Grundgedanke
Die Romberg-Integration basiert auf der Richardson-Extrapolation zum Limes über die Schrittweite einer summierten Quadraturformel, wie beispielsweise der Trapezregel. Die Trapezregel ist hier besonders zu erwähnen, da sie einfach zu berechnen ist und zudem eine Entwicklung in quadratischen Potenzen der Schrittweite besitzt, also eine Extrapolation in Quadraten der Schrittweite möglich ist, die deutlich schneller konvergiert als die einfache Extrapolation zum Limes. Mit Schrittweite h ist hier die Breite der Trapeze bei der Trapezregel gemeint.
Der aufwändige Teil der numerischen Integration sind oft die Funktionsauswertungen. Um deren Anzahl minimal zu halten, ist es somit ratsam, einen Schrittweitenverlauf zu wählen, der die Weiterverwendung von bereits berechneten Funktionswerten erlaubt. Ein Beispiel für eine solche Schrittweite wäre
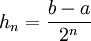 , das zugleich die Bedingungen für eine konvergente Extrapolation erfüllt. Also
, das zugleich die Bedingungen für eine konvergente Extrapolation erfüllt. Also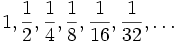
Bei dieser sogenannten Romberg-Folge wächst die Anzahl der benötigten Funktionsauswertungen bei großen n schnell an, was nicht immer erwünscht ist.
Um diesem abzuhelfen, kann auch die Bulirsch-Folge verwendet werden:
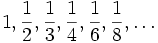
Hier werden Glieder mit
 zwischengeschaltet.
zwischengeschaltet.Rechenvorschrift
mit
dabei ist
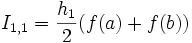 (Trapezregel)
(Trapezregel)
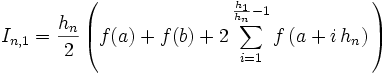 (aufsummierte Trapezregel mit mehrfachen Intervallen)
(aufsummierte Trapezregel mit mehrfachen Intervallen)
und
- hn die im n-ten Schritt verwendete Schrittweite (siehe oben)
das Fehlerglied hat den Wert:
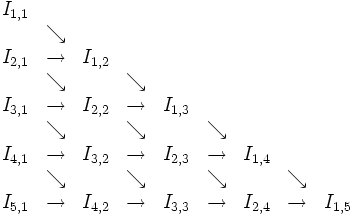
Vorgehensweise
- Zuerst wird I1,1 berechnet.
- Beginne eine zyklische Berechnung (Hauptzyklus) mit der Zyklusvariablen n mit n = 1 und berechne In + 1,1. Nutze dabei Werte aus den vorhergehenden Zyklen aus, abhängig von der verwendeten Schrittweiten-Folge.
- Extrapoliere in einem Unterzyklus mit
k = 2 bis n + 1unds = 2 + n - k
den Wert Is,k nach obiger Regel - Berechne die Genauigkeit. Ist die gewünschte Genauigkeit noch nicht erreicht, so erhöhe n um 1 und setze den Hauptzyklus mit einem neuen Durchgang fort.
Die Berechnung startet also wie folgt (Romberg-Folge):- Berechnen von I1,1 nach der Trapezregel
- Hauptzyklus starten mit n = 1
- Berechnen von In + 1,1 = I2,1 nach der Trapezregel (2 Intervalle, 21 = 2). Es muss nur der mittlere Funktionswert neu berechnet werden:
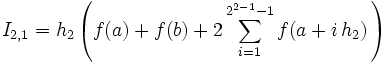
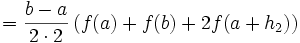
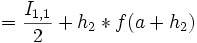
- Unterzyklus: k geht von 2 bis 2 .
- Neuer Durchgang des Hauptzyklus mit n = 2 .
- Berechnen von
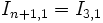 nach der Trapezregel (4 Intervalle, 22 = 4, zwei neue Funktionswerte).
nach der Trapezregel (4 Intervalle, 22 = 4, zwei neue Funktionswerte).
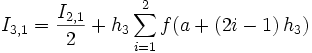
- Unterzyklus: k geht von 2 bis 3 .
-
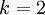 und
und 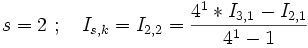
-
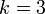 und
und 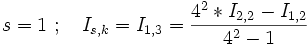
- Neuer Durchgang des Hauptzyklus mit n= 3 .
- Berechnen von In + 1,1 = I4,1 nach der Trapezregel 8 Intervalle, 23 = 8, 4 neue Funktionswerte).
- Unterzyklus: k geht von 2 bis 4 .
-
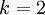 und
und 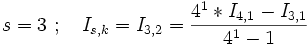
-
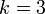 und
und 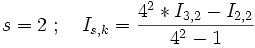
-
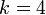 und
und 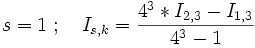
- Neuer Durchgang des Hauptzyklus mit n = 4
- usw.
Quellcode
// java source code public interface numericalIntegrationInterface { public double computeFunction(double x); } public class numericalIntegration { // a ... integral from // b ... integral to double a,b; // the function of which we want to compute the area numericalIntegrationInterface f; public numericalIntegration(double rangeFrom, double rangeTo, numericalIntegrationInterface function) { a = rangeFrom; b = rangeTo; if (a > b) { double temp = a; a = b; b = temp; } f = function; } private int pow(int a, int b) { if (b == 0) return 1; if (b == 1) return a; int result = a; for (int i = 1; i < b; i++) result *= a; return result; } private double computeI_n_k(int n, int k, double I[][]) { return (pow(4,k-1)*I[n+1][k-1]-I[n][k-1])/(pow(4,k-1) - 1.0); } private double computeI_n_1(int n) { double temp = 0; int steps = pow(2,n); for (int i = 1; i <= steps-1; i++) temp += f.computeFunction(a + ((i * (b-a))/ steps ) ); return ((b-a)/(2*steps)) * (f.computeFunction(a) + f.computeFunction(b) + 2*temp); } private double computeError(int n, double I[][]) { return (I[1][n+1] - I[1][n])/I[1][n]; } public double computeAreaRomberg(double maxError, int minIt, int maxIt) { if (a == b) return 0.0; double I[][] = new double[maxIt+2][maxIt+2]; double error = Double.MAX_VALUE; int n,s,k; I[1][1] = ((b-a)/2.0) * (f.computeFunction(a) + f.computeFunction(b)); for (n = 1; (n <= minIt || error > maxError) && n <= maxIt; n++) { I[n+1][1] = computeI_n_1(n); for (k = 2; k <= n+1; k++) { s = 2 + n - k; I[s][k] = computeI_n_k(s,k,I); } error = Math.abs(computeError(n,I)); } return I[n][1]; } }
Anmerkungen
Eine Unterschreitung der hier definierten Fehlerschranke bedeutet nicht immer, dass das Integral korrekt berechnet wurde. Dies gilt besonders für periodische Funktionen und Funktionen mit einem periodischen Anteil. So führt z. B. das bei der Fourier-Analyse periodischer Funktionen vorkommende Integral
u. U. zu einem Fehler, wenn man nicht mindestens n+1 Integrationsstufen berechnet. In den ersten n Integrationsstufen fallen alle Stützstellen mit den Nullstellen der Funktion zusammen. Als Integral erhält man daher immer den Wert Null, egal ob es stimmt oder nicht. Ein Computerprogramm sollte also immer eine Mindestanzahl an Integrationsstufen erzwingen.
Fazit
Der große Vorteil der Romberg-Quadratur gegenüber anderen Verfahren besteht in der Möglichkeit, den Fehler im Nachhinein zu kontrollieren und schon erreichte Ergebnisse weiterzuverwenden, wenn die Genauigkeit noch nicht erreicht ist.
Weblinks
- Romberg-Integration – Plugin für Yacas
Wikimedia Foundation.

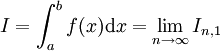
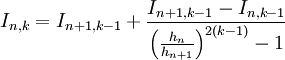
![k \in [ 1 , n+1] \quad \in \mathbb{N}](/pictures/dewiki/101/e03a38c945dccac07db598e3d45ce50a.png)