Rytzsche Achsenkonstruktion

Mit Hilfe der rytzschen Achsenkonstruktion ist es möglich, ausgehend von zwei konjugierten Durchmessern einer Ellipse deren Haupt- und Nebenachse und die zugehörigen Ellipsenscheitel zu finden. Bei der rytzschen Achsenkonstruktion handelt es sich um eine klassische Konstruktion der euklidischen Geometrie, bei der nur Zirkel und Lineal als Hilfsmittel erlaubt sind. Die Konstruktion ist benannt nach ihrem Erfinder David Rytz von Brugg, 1801 - 1868.

Problemstellung

Abbildung 1: Gegebene Größen und Ergebnisse

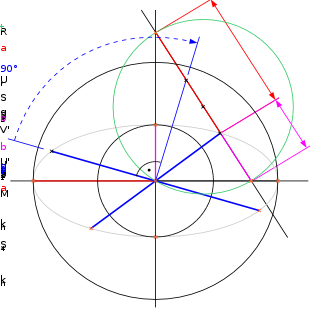
Abbildung 1 zeigt die gegebenen und gesuchten Größen. Gegeben sind die beiden konjugierten Durchmesser d₁' und d₂' (blau), gesucht sind die Achsen a und b der Ellipse (rot). Zur Verdeutlichung ist die zugehörige Ellipse e ebenfalls eingezeichnet, sie ist allerdings weder gegeben, noch ist sie ein direktes Ergebnis der rytzschen Achsenkonstruktion. Mit Zirkel und Lineal lassen sich nur einzelne Ellipsenpunkte konstruieren, nicht aber die gesamte Ellipse. Verfahren zum Zeichnen einer Ellipse setzen in der Regel die Achsen der Ellipse als gegeben voraus. Sind nicht die Achsen sondern nur zwei konjugierte Durchmesser einer Ellipse gegeben, kann die Rytzsche Achsenkonstruktion als Vorverarbeitungsschritt zur Darstellung der Ellipse betrachtet werden.

Konjugierte Durchmesser

Eine Ellipse kann als affines Bild ihres Hauptkreises betrachtet werden. Abbildung 1 zeigt neben der Ellipse e ihren Hauptkreis k_h. Die Affine Abbildung α, welche k_h in e überführt ist durch gestrichelte Pfeile angedeutet. Das Urbild eines Ellipsendurchmessers unter der Abbildung α ist ein Kreisdurchmesser von k_h. Die definierende Eigenschaft konjugierter Durchmesser d₁' und d₂' einer Ellipse ist, dass ihre Urbilder d₁ und d₂ aufeinander senkrecht stehen. So gesehen sind die Achsen einer Ellipse spezielle konjugierte Durchmesser, bei denen nicht nur ihre Urbilder sondern die Durchmesser selbst aufeinander senkrecht stehen. Die Rytzsche Achsenkonstruktion findet zu zwei beliebigen konjugierten Durchmessern diejenigen konjugierten Durchmesser der zugehörigen Ellipse, die aufeinander senkrecht stehen. Diese speziellen konjugierten Durchmesser sind die Achsen der Ellipse.

Konstruktion

Abbildung 2: Konstruktion

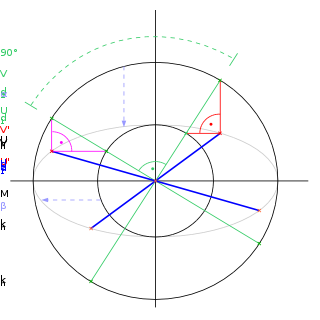
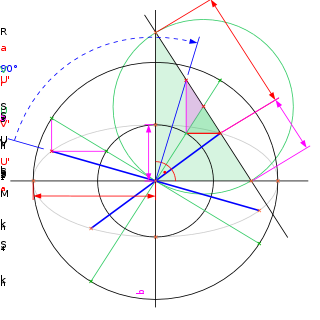
Abbildung 2 zeigt die Schritte der Rytzschen Achsenkonstruktion. Gegeben sind die fett blau eingezeichneten konjugierten Durchmesser d₁' und d₂', die sich im Mittelpunkt M der Ellipse schneiden. Von jedem konjugierten Durchmesser wird ein Endpunkt gewählt: U' auf d₁' und V' auf d₂'. Der Winkel $\angle(U' M V')$ ist entweder stumpf ($> 90^\circ$) wie in der Abbildung, oder spitz ($< 90^\circ$). Stünden die konjugierten Durchmesser aufeinander senkrecht ($= 90^\circ$), wären die Achsen bereits gefunden: In diesem Fall wären sie identisch mit den gegebenen konjugierten Durchmessern.

Im ersten Schritt wird U' um den Mittelpunkt M um $90^\circ$ in Richtung V' gedreht. Das Ergebnis ist der Punkt U'_r. Die Punkte U'_r und V' definieren die Gerade g. Der Mittelpunkt der Strecke $\overline{U'_r V'}$ sei S. Im nächsten Schritt schlägt man einen Kreis t um S, so dass dieser durch den Mittelpunkt M der Ellipse verläuft. Die Schnittpunkte dieses Kreises mit der Geraden g definieren die Punkte R und L. R und L werden so gewählt, dass, vom Punkt S aus gesehen der Punkt R auf derselben Seite wie U'_r liegt und L auf derselben Seite wie V'. Man zeichnet als nächstes vom Punkt M aus zwei Geraden, eine durch R und die andere durch L. Diese Geraden schneiden sich in M in einem rechten Winkel (da t ein zugehöriger Thaleskreis ist).

Die Aussage der Rytzschen Achsenkonstruktion ist nun, dass die Ellipsenachsen auf den Geraden durch M und R bzw. M und L liegen, und dass die Länge der Strecke $\overline{V' R}$ der Länge a des Ellipsen-Hauptscheitels und $\overline{V' L}$ der Länge b des Ellipsen-Nebenscheitels entspricht. Im letzten Schritt schlägt man daher zwei Kreise um M mit den Radien a und b. Man findet die Hauptscheitelpunkte S₁ und S₂ im Abstand a von M auf der Geraden durch L und entsprechend die Nebenscheitelpunkte S₃ und S₄ im Abstand b von M auf der geraden durch R.

Begründung der Konstruktion

Die Rytzsche Achsenkonstruktion beruht auf den Eigenschaften konjugierter Ellipsendurchmesser und ist ohne Betrachtung der Ellipse als affines Kreisbild nicht einsichtig. Dieser Abschnitt gibt einen Einblick in die Hintergründe der Konstruktion und erlaubt es, ihre Korrektheit zu verstehen. Das Lesen dieses Abschnitts ist nicht notwendig, um die Konstruktion auszuführen. Dieser Abschnitt geht davon aus, dass neben den gegebenen konjugierten Durchmessern das Ergebnis der Konstruktion (die Ellipsenachsen und Scheitel) bereits bekannt ist, um anhand dessen die Konstruktionsschritte einsichtig zu machen.

Die Urbilder der konjugierten Durchmesser

Abbildung 3: Urbilder der konjugierten Durchmesser

Die Ellipse, deren konjugierten Durchmesser d₁' und d₂' gegeben sind, kann als affines Bild ihres Hauptkreises bezüglich einer affinen Abbildung α betrachtet werden. Abbildung 3 zeigt die Ellipse mit ihrem Hauptkreis k_h und ihrem Nebenkreis k_n. Die Punkte U' und V' seien Endpunkte von d₁' bzw. d₂', die sich im Mittelpunkt M des Hauptkreises schneiden. Die Urbilder d₁ und d₂ (grün) von d₁' und d₂' bezüglich α sind damit Kreisdurchmesser des Ellipsen-Hauptkreises k_h. Aufgrund der Eigenschaft, dass d₁' und d₂' konjugierte Durchmesser sind, stehen ihre Urbilder d₁ und d₂ aufeinander senkrecht. Das Urbild von U' bzw. V' bezüglich α sind die korrespondierenden Endpunkte U bzw. V der Kreisdurchmesser d₁ bzw. d₂. Die Schnittpunkte der Kreisdurchmesser d₁ bzw. d₂ mit dem Nebenkreis k_n der Ellipse seien die Punkte U_n bzw. V_n.

Zu Beginn der Konstruktion sind nur die Punkte M, U' und V' gegeben. Weder die Urbilder d₁ und d₂ der konjugierten Durchmesser, noch die Punkte U, U_n, V und V_n sind bekannt, noch werden sie im Verlauf der Konstruktion bestimmt. Sie sind lediglich für das Verständnis der Konstruktion wichtig. Wenn im weiteren Verlauf der Beschreibung auf diese Punkte Bezug genommen wird, ist das zu verstehen als „Wenn diese Punkte bekannt wären, dann würde man feststellen dass...“.

Parallelen zu den Ellipsenachsen

Abbildung 4: Parallelen zu den Ellipsenachsen

Interessanterweise sind die Strecken $\overline{U U'}$ und $\overline{U' U_n}$ parallel zu den Ellipsenachsen und bilden daher einen rechten Winkel in U'. Gleiches gilt für die Strecken $\overline{V V'}$ und $\overline{V' V_n}$ im Punkt V'. Dies kann folgendermaßen erklärt werden: Die affine Abbildung α, welche den Ellipsenhauptkreis auf die Ellipse abbildet, hat die Nebenachse der Ellipse als Fixgerade. Da eine Gerade durch einen Punkt (beispielsweise U) und seinen Bildpunkt (beispielsweise U') ebenfalls eine Fixgerade ist, muss aufgrund der Parallelentreue affiner Abbildungen, die Gerade durch U und U' eine Parallele zur Nebenachse sein. Dasselbe Argument gilt für die Gerade durch V und V'. Um zu zeigen, dass die Geraden durch U_n und U' bzw. V_n und V' parallel zur Ellipsenhauptachse sind, betrachtet man die Ellipse als affines Bild ihres Nebenkreises und wendet das Argument entsprechend an.

Die Erkenntnis, dass die Strecken $\overline{U U'}$ und $\overline{U' U_n}$ parallel zu den gesuchten Achsen liegen hilft noch nicht weiter, da die Punkte U und U_n nicht bekannt sind. Der folgende Schritt nutzt diese Parallelitäten allerdings geschickt aus, um dennoch die Achsen zu finden.

Finden der Ellipsenachsen

Abbildung 5: Finden der Ellipsenachsen

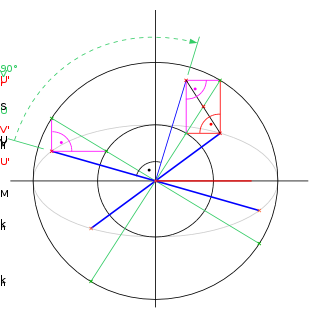
Dreht man, wie in Abbildung 3 gezeigt, den Ellipsendurchmesser d₁' mitsamt seinem Urbild d₁ um $90^\circ$ um den Mittelpunkt M in Richtung V', so kommt d₁ mit d₂ zur Deckung und der gedrehte Punkt U fällt mit V und U_n mit V_n zusammen. Der Punkt U' geht in U'_r über. Aufgrund der Parallelität von $\overline{U' U_n}$ und $\overline{V' V_n}$ mit einer Ellipsenachse und der Parallelität von $\overline{U U'}$ und $\overline{V V'}$ mit der anderen Ellipsenachse bilden die Punkte U'_r, V, V' und V_n ein Rechteck. Von diesem Rechteck, sind allerdings nur die Punkte V' und U'_r bekannt. Dies reicht aber aus, um seinen Diagonalenschnittpunkt zu finden.

Der Diagonalenschnittpunkt S ergibt sich durch Halbierung der Diagonale $\overline{U'_r V'}$. Die andere Diagonale liegt auf der Geraden durch M und S (weil S der Diagonalenschnittpunkt ist und die Diagonale auf einem Durchmesser des Hauptkreises liegen muss), allerdings sind ihre Endpunkte V und V_n durch die Konstruktion noch nicht identifiziert. 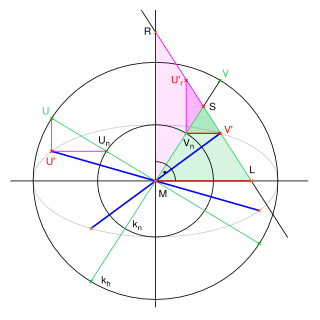Wichtig zum Finden der Ellipsenachsen ist aber lediglich, dass die Ellipsenhauptachse eine Parallele zu $\overline{V' V_n}$ durch M ist und entsprechend die Ellipsen-Nebenachse eine Parallele zu $\overline{U'_r V_n}$ durch M ist.

Verlängert man die bereits bekannte Diagonale $\overline{U'_r V'}$ wie in Abbildung 4, so schneidet sie die Ellipsen-Hauptachse in einem Punkt L und die Ellipsen-Nebenachse in R, und es entstehen gleichschenklige Dreiecke $\triangle(S V_n V')$ und $\triangle(S M L)$ in S (die Diagonalen teilen ein Rechteck in vier gleichschenklige Dreiecke, plus Strahlensatz). Selbiges gilt für die Dreiecke $\triangle(S V_n U'_r)$ und $\triangle(S M R)$. Diese Eigenschaft wird für die Konstruktion der Punkte L und R ausgenutzt: Da die Länge der Strecke $\overline{S M}$ gleich der Länge der Strecken $\overline{S L}$ bzw. $\overline{S R}$ sein muss, findet man L bzw. R als Schnittpunkte eines Kreises um S mit Radius $\overline{S M}$. Mit den Punkten L und R ist jetzt auch die Lage der Ellipsenachsen bekannt (auf den Geraden durch M und L bzw. R). Es fehlt lediglich die Scheitelpunkte.

Identifikation der Ellipsenscheitel

Abbildung 6: Identifikation der Scheitelpunkte

Die Länge der Hauptachse a entspricht der Länge des Radius es Hauptkreises. Die Länge der Nebenachse b ist gleich dem Radius des Nebenkreises. Der Radius des Hauptkreises ist aber gleich der Länge der Strecke $\overline{M V}$ und der Radius des Nebenkreises ist gleichder Länge der Strecke $\overline{M V_n}$. Zur Bestimmung von a und b muss die Lage der Punkte V und V_n nicht konstruiert werden, da folgende Identitäten gelten:

$a = \left| \overline{M V} \right| = \left| \overline{M S} \right| + \left| \overline{S V} \right| = \left| \overline{R S} \right| + \left| \overline{S V} \right| = \left| \overline{R S} \right| + \left| \overline{S V'} \right| = \left| \overline{R V'} \right|$

$b = \left| \overline{M V_n} \right| = \left| \overline{M S} \right| - \left| \overline{S V_n} \right| = \left| \overline{S L} \right| - \left| \overline{S V_n} \right| = \left| \overline{S L} \right| - \left| \overline{S V'} \right| = \left| \overline{V' L} \right|$

In der Konstruktion lässt sich also die Länge der Ellipsenachsen bereits ablesen: $a = \left| \overline{R V'} \right|$ und $b = \left| \overline{V' L} \right|$. Mit dieser Information lassen sich der Haupt- und Nebenkreis der Ellipse einzeichnen. Die Hauptscheitelpunkte S₁ und S₂ findet man als Schnittpunkte des Hauptkreises mit der der Ellipsenhauptachse. Die Entscheidung, bei welcher der beiden gefundenen Achsen es sich um die Haupt- bzw. die Nebenachse handelt, begründet sich wie folgt: V' ist das Bild von V bezüglich der affinen Abbildung α, die den Ellipsen-Hauptkreis auf die Ellipse abbildet. Da es sich bei α und eine Kontraktion in Richtung der Hauptachse handelt, muss sich die Hauptachse auf der V gegenüberliegenden Seite von d₂' befinden und damit durch den Punkt L verlaufen, der auf der Seite des nicht gedrehten Ellipsendurchmessers d₂' liegt. Dies ist unabhängig von der initialen Wahl der Punkte U' und V'. Entscheidend ist allein, dass U' bei der Drehung um $90^\circ$ auf V' zugedreht wird, da nur dann der Punkt S auf dem Urbild d₂ des konjugierten Durchmessers d₂' liegt. Die Ellipsen-Hauptachse liegt dann von V' aus betrachtet immer auf der S gegenüberliegenden Seite von d₂'.