- Scheitelpunkt
-
Scheitelpunkte, kurz Scheitel, sind ausgezeichnete Punkte in der Geometrie.
Inhaltsverzeichnis
Scheitelpunkt eines Winkels
Unter dem Scheitelpunkt eines Winkels versteht man den gemeinsamen Anfangspunkt der beiden Schenkel (also der begrenzenden Halbgeraden oder Strahlen) dieses Winkels.
Scheitelpunkt eines Kegelschnitts
Die Scheitelpunkte eines Kegelschnitts sind die Schnittpunkte einer solchen Kurve mit deren Symmetrieachsen. Die Ellipse hat vier Scheitel, zwei Hauptscheitel und zwei Nebenscheitel, bei der Hyperbel treten zwei auf, bei der Parabel nur einer, der Kreis hat keinen expliziten Scheitelpunkt.
Scheitelpunkt einer Parabel
Der Scheitelpunkt einer Parabel in der Analysis ist identisch mit dem Hochpunkt (Maximum), wenn sie nach unten geöffnet ist, und identisch mit dem Tiefpunkt (Minimum), wenn die Parabel nach oben geöffnet ist.
Wenn die Lage des Scheitelpunktes bekannt ist, kann die Parabel, soweit es sich um eine Normalparabel handelt, mit Hilfe einer Parabelschablone schnell in ein Koordinatensystem gezeichnet werden.
Scheitelpunktform
Eine Parabel entspricht einer quadratischen Funktion, also einem Polynom zweiten Grades und kann daher in der Form
 ausgedrückt werden.
ausgedrückt werden.Unter der Scheitelform oder Scheitelpunktform einer quadratischen Funktion versteht man eine bestimmte Form dieser Gleichung, aus welcher man den Scheitelpunkt der Funktion direkt ablesen kann.
Sie lautet
 mit dem Scheitelpunkt
mit dem Scheitelpunkt  .
.Folglich kann die Funktion
 in die Form
in die Form  überführt werden.
überführt werden.Der Scheitelpunkt lautet dann
 .
.In der Schule wird diese Formel aufgrund ihrer Größe meistens nicht gelehrt. Stattdessen wird die quadratische Ergänzung gelehrt, mit deren Hilfe man eine quadratische Funktion in der Polynomform in die Scheitelpunktform überführt.
Herleitung mittels quadratischer Ergänzung
Die obige Formel kann mithilfe der quadratischen Ergänzung hergeleitet werden. Die Normalform wird in die Scheitelpunktform umgeformt.
Daraus können die Koordinaten des Scheitelpunktes direkt abgelesen werden:
 .
.Herleitung mittels Ableitung
Da die Steigung im Scheitelpunkt gleich 0 ist, ist es möglich mit Hilfe der ersten Ableitung die obige Formel herzuleiten.
Einsetzen in die Normalform:
Beispiele
Beispiel 1
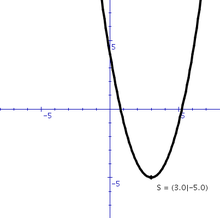
- f(x) = x2 − 6x + 4
hat den Scheitelpunkt:
 , mit der Lösung: S(3 | − 5)
, mit der Lösung: S(3 | − 5)
Beispiel 2
- f(x) = − x2 + 3x + 4
Da diese nicht in der Normalform vorliegt, kann man die Lösung nur durch Umformung hin zur Scheitelpunktform finden.
Scheitelpunkt ist:

Motorsport
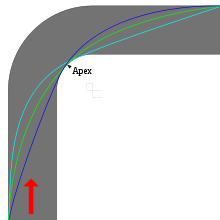
Der Scheitelpunkt einer Kurve liegt nahe dem oben dargestellten Punkt einer Parabel, in dem das Fahrzeug den Innenrand der Fahrbahn erreicht. Die Kurve ist eher kreisförmig; allerdings ist der Radius im Kurveneingang enger, vergrößert sich nach dem Scheitelpunkt wieder und ähnelt dadurch einer ballistischen Parabel. Auch liegt der für die Geschwindigkeit beste Scheitelpunkt nicht dort, wo die geometrische Mitte der Kurve liegt, sondern etwas dahinter. Als Grund muss gelten, dass die Summe der Kurvenradien im langsameren Kurveneingang kleiner sein sollte als im schnelleren Kurvenausgang (Ideallinie).[1] Es handelt sich um die hellblaue Linie in nebenstehendem Bild.
Weblinks
Einzelnachweise
Wikimedia Foundation.