- Halbachsen der Ellipse
-
Die große Halbachse ist die halbe Länge des größten Durchmessers einer Ellipse, der auch Hauptachse genannt wird. Der kürzeste halbe Durchmesser, der genau im Winkel von 90° dazu steht, wird kleine Halbachse genannt. Der Kreis ist eine spezielle Ellipse, bei der diese beide Halbachsen gleich lang sind, in diesem Fall entspricht die Halbachse dem Radius des Kreises.
 Parameter einer Ellipse:
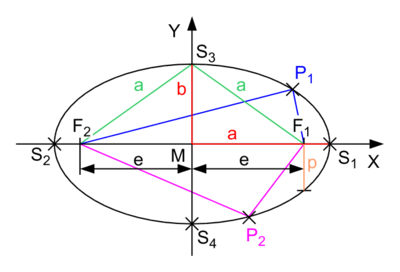
Parameter einer Ellipse:
S1,S2 Hauptscheitel S3,S4 Nebenscheitel S1S2 Hauptachse S3S4 Nebenachse a Große Halbachse b Kleine Halbachse F1,F2 Brennpunkte e lin. Exzentrizität M Mittelpunkt p Parameter (semi-latus rectum) Die Hauptachse (hier S1S2) und die Nebenachse (der kleinste Durchmesser, hier S3S4) werden manchmal auch gemeinsam als die Hauptachsen der Ellipse bezeichnet. Haupt- und Nebenachse sind konjugierte Durchmesser. Diese Beziehung bleibt auch bei „schräger“ Betrachtungsweise der Ellipse erhalten, was zur geometrischen Konstruktion von anderen konjugierten Durchmessern genutzt werden kann.
Astronomie
In der Astronomie ist die große Halbachse einer keplerschen Umlaufbahn eines der sechs sogenannten Bahnelemente und wird oft auch als „mittlere Entfernung“ angegeben und meistens mit a abgekürzt. Sie charakterisiert – zusammen mit der Exzentrizität – die Form von elliptischen Umlaufbahnen verschiedener Himmelskörper.
Solche Körper sind in erster Linie die Planeten und ihre Monde, künstliche Erdsatelliten, die Asteroiden und tausende Doppelsterne.
Nach dem dritten Gesetz von Kepler ist die Umlaufzeit U einer Ellipsenbahn mit a gekoppelt (U² / a³ = const). Die Konstante hängt mit der Masse des Zentralkörpers zusammen – in einem Planetensystem also mit der Masse des Zentralsterns.
Die beiden Hauptscheitel nennt man Apsiden, die Hauptachse ist die Apsidenlinie: Wenn ein Körper im Brennpunkt F1 liegt und ein kleinerer Körper ihn auf einer Ellipse umkreist, so spricht man beim kürzesten Abstand (F1S1=a−e) von der Periapsis und beim längsten Abstand (F1S2=a+e) von der Apoapsis (Perihel, Aphel bei der Sonne).
In der Periapsis (Perizentrum, gravizentrumsnaher Hauptscheitel) ist die Orbitalgeschwindigkeit maximal, im Apozentrum minimal.
Geodäsie
In der Geodäsie sind die Achsen der sogenannten Fehlerellipsen ein wichtiges Darstellungsmittel der mittleren beziehungsweise maximalen/minimalen Punktfehler. Bei der Ausgleichung von geodätischen Netzen lässt sich die Genauigkeit, mit der die einzelnen Vermessungspunkte des Netzes bestimmt sind, als Fehlerellipse darstellen.[1]
Einzelnachweise
- ↑ Erwin Groten: Zur Definition des mittleren Punktfehlers. In: Zeitschrift für Vermessungswesen (ZfV). 11/1969. S. 455–457
Wikimedia Foundation.
