SHA1

Der Begriff secure hash algorithm (engl. für sicherer Hash-Algorithmus), kurz SHA, bezeichnet eine Gruppe standardisierter kryptologischer Hash-Funktionen. Diese dienen zur Berechnung eines eindeutigen Prüfwerts für beliebige elektronische Daten. Meist handelt es sich dabei um Nachrichten. Es soll praktisch unmöglich sein, zwei verschiedene Nachrichten mit dem gleichen SHA-Wert zu finden. Dieses wird auch als Kollisionsfreiheit bezeichnet. Ob SHA-1 dieser Anforderung genügt, kann nicht sicher gesagt werden, da im Sommer 2006 eine wesentliche Schwäche dieses Algorithmus entdeckt und publik gemacht wurde. Grundsätzlich sollte SHA-1 daher nicht mehr in neuen Entwicklungen als sicherer Hash-Algorithmus vorgesehen werden.

Aufbau einer Runde von SHA-1

Aufbau einer Runde von SHA-2

Das NIST (National Institute of Standards and Technology) entwickelte zusammen mit der NSA (National Security Agency) eine zum Signieren gedachte sichere Hash-Funktion als Bestandteil des Digital Signature Algorithms (DSA) für den Digital Signature Standard (DSS). Die Funktion wurde 1994 veröffentlicht. Diese als Secure Hash Standard (SHS) bezeichnete Norm spezifiziert den sicheren Hash-Algorithmus (SHA) mit einem Hash-Wert von 160 Bit Länge für beliebige digitale Daten von maximal 2⁶⁴ − 1 Bit (≈ 2 Exbibyte) Länge. Intern werden Blöcke der Größe 512 Bit (64 Bytes) verwendet. Der Algorithmus ähnelt im Aufbau dem von Ronald L. Rivest entwickelten MD4. Der SHA wurde wegen eines „Designfehlers“ 1995 korrigiert. Diese neue Variante ist heute als SHA-1 bekannt, die ursprüngliche als SHA-0. Sie unterscheiden sich nur in einem kleinen Detail (Linksshift), nicht jedoch in der Anzahl der durchlaufenen Runden oder sonstiger Maßnahmen, die unmittelbar eine wesentlich höhere Sicherheit erwarten lassen. Die Kryptoanalyse bestätigt jedoch, dass der Linksshift die Berechnung von Kollisionen offenbar erheblich erschwert.

Prinzipiell wurde von den gleichen Entwurfszielen wie beim MD4 ausgegangen. Mit seinem längeren Hash-Wert von 160 Bit ist SHA aber widerstandsfähiger gegen Brute-Force-Angriffe zum Auffinden von Kollisionen.

Erweiterungen

Das NIST hat im August 2002 drei weitere Varianten des Algorithmus veröffentlicht, die größere Hash-Werte erzeugen. Es handelt sich dabei um den SHA-256, SHA-384 und SHA-512 wobei die angefügte Zahl jeweils die Länge des Hash-Werts (in Bit) angibt. Mit SHA-384 und SHA-512 können (theoretisch) Daten bis zu einer Größe von 2¹²⁸ Bit verarbeitet werden. In der Praxis sind Dateien mit mehr als 2⁶⁴ Bit jedoch unrealistisch. Im Februar 2004 wurde eine weitere Version, SHA-224, veröffentlicht.

Die Algorithmen SHA-1 und SHA-256 sind auch die Basis für die Blockverschlüsselung SHACAL. Alle diese Weiterentwicklungen werden manchmal auch unter dem Begriff SHA-2 zusammengefasst.

Zur Erzeugung des Hash-Wertes bei SHA-256 werden die Quelldaten in 512-Bit-Blöcke bzw. 16 32-Bit-Wörter aufgeteilt und iterativ mit 64 Konstanten und sechs logischen Funktionen verrechnet. Dabei wird mit einem Start-Hash aus acht 32-Bit-Wörtern begonnen. Dazu werden die ersten 32 Bits des Nachkommateils der Quadratwurzeln der ersten acht Primzahlen (2 bis 19) verwendet.

Bei SHA-224 wird exakt der gleiche Algorithmus verwendet, der Initialhash wird jedoch mit acht anderen Werten gesetzt (Bits 33 bis 64 der Nachkommastellen der Quadratwurzeln der Primzahlen ab 23). Beim Endergebnis wird einfach das achte 32-Bit-Wort weggelassen.

Bei SHA-512 wird mit 1024-Bit-Blöcken und einer Wortbreite von 64 Bit gearbeitet. Es werden 80 64-Bit-Konstanten und sechs logische Funktionen verwendet. Der Initialhash besteht aus acht 64-Bit-Werten, wobei auch hier die Nachkommastellen der Quadratwurzeln der ersten acht Primzahlen herangezogen werden.

Für SHA-384 gilt der gleiche Algorithmus. Der Initialhash wird allerdings aus den 64 Nachkommabits der Quadratwurzeln der nachfolgenden Primzahlen (23, 29 usw.) berechnet. Am Ende werden vom Ergebnis nur die ersten sechs 64-Bit-Wörter genommen.

Schwächen

Am 15. Februar 2005 meldete der Kryptographieexperte Bruce Schneier in seinem Blog, dass die Wissenschaftler Xiaoyun Wang, Yiqun Lisa Yin und Hongbo Yu an der Shandong University in China erfolgreich SHA-1 gebrochen hätten. Ihnen sei es gelungen, den Aufwand zur Kollisionsberechnung von 2⁸⁰ auf 2⁶⁹ zu verringern. 2⁶⁹ Berechnungen könnten eventuell mit Hochleistungsrechnern durchgeführt werden. Kollisionen wurden aber bis heute nicht veröffentlicht.

Kurze Zeit später, am 17. August 2005, wurde von Xiaoyun Wang, Andrew Yao und Frances Yao auf der Konferenz CRYPTO 2005 ein weiterer, effizienterer Kollisionsangriff auf SHA-1 vorgestellt, welcher den Berechnungsaufwand auf 2⁶³ reduziert.

Im August 2006 wurde auf der CRYPTO 2006 ein weiterer, wesentlich schwerwiegenderer Angriff gegen SHA-1 präsentiert, der möglicherweise auch in der Praxis Auswirkungen zeigen kann. Bei diesem Angriff kann ein Teil der gefälschten Nachricht (derzeit bis zu 25 %) im Inhalt frei gewählt werden. Bei den bisherigen Kollisionsangriffen wurden die so genannten Hash-Zwillinge lediglich mit sinnlosen Buchstabenkombinationen des Klartextes gebildet und waren damit leicht zu erkennen.

Ein kritisches Angriffsszenario setzt aber voraus, dass der Angreifer eine zweite, zumindest in Teilen sinnvolle Variante eines Dokuments erzeugen kann, die den gleichen SHA-1-Wert und damit auch die gleiche Signatur ergibt. Die bei der neuen Angriffsmethode derzeit verbleibenden 75 % sinnloser Buchstabenkombinationen (also Datenmüll) können vor den Augen eines ungeschulten Betrachters ggf. technisch leicht verborgen werden. Der Angreifer kann daher behaupten, die gefälschte Variante sei an Stelle der originalen Variante signiert worden.

Momentan (Stand 2008) versucht eine Forschungsgruppe der Technischen Universität Graz, mittels eines Distributed Computing-Projektes Kollisionen im SHA-1-Algorithmus zu finden (SHA-1 Collision Search Graz).

Empfehlungen

Als Reaktion auf die bekanntgewordenen Angriffe gegen SHA-1 hielt das National Institute of Standards and Technology (NIST) im Oktober 2005 einen Workshop ab, in dem der aktuelle Stand kryptologischer Hashfunktionen diskutiert wurde. NIST empfiehlt den Übergang von SHA-1 zu Hashfunktionen der SHA-2-Familie (SHA-224, SHA-256, SHA-384, SHA-512). Langfristig sollen diese durch einen neuen Standard SHA-3 ersetzt werden. Dazu ruft das NIST nach Vorbild des Advanced Encryption Standard (AES) zu einem Ausschreiben auf. Die endgültige Wahl und Benennung des Hash-Standards ist für 2012 vorgesehen.

Beispiel-Hashes

SHA-1

SHA1("Franz jagt im komplett verwahrlosten Taxi quer durch Bayern")
 = 68ac906495480a3404beee4874ed853a037a7a8f

Eine kleine Änderung der Nachricht erzeugt (mit sehr großer Wahrscheinlichkeit) einen komplett anderen Hash. Mit Frank statt Franz (nur ein Buchstabe verändert) ergibt sich:

SHA1("Frank jagt im komplett verwahrlosten Taxi quer durch Bayern")
 = d8e8ece39c437e515aa8997c1a1e94f1ed2a0e62

Der Hash eines Strings der Länge Null ist:

SHA1("")
 = da39a3ee5e6b4b0d3255bfef95601890afd80709

SHA-2

SHA-2 bildet eine Familie von Algorithmen, die sich durch die Länge des Hash-Werts unterscheiden. Damit kann eine Abwägung zwischen Rechenaufwand und Sicherheit getroffen werden.

SHA-224

SHA224("Franz jagt im komplett verwahrlosten Taxi quer durch Bayern")
 = 49b08defa65e644cbf8a2dd9270bdededabc741997d1dadd42026d7b

SHA224("Frank jagt im komplett verwahrlosten Taxi quer durch Bayern")
 = 58911e7fccf2971a7d07f93162d8bd13568e71aa8fc86fc1fe9043d1

Der Hash eines Strings der Länge Null ist:

SHA224("")
 = d14a028c2a3a2bc9476102bb288234c415a2b01f828ea62ac5b3e42f

SHA-256

SHA256("Franz jagt im komplett verwahrlosten Taxi quer durch Bayern")
 = d32b568cd1b96d459e7291ebf4b25d007f275c9f13149beeb782fac0716613f8

SHA256("Frank jagt im komplett verwahrlosten Taxi quer durch Bayern")
 = 78206a866dbb2bf017d8e34274aed01a8ce405b69d45db30bafa00f5eeed7d5e

Der Hash eines Strings der Länge Null ist:

SHA256("")
 = e3b0c44298fc1c149afbf4c8996fb92427ae41e4649b934ca495991b7852b855

SHA-384

SHA384("Franz jagt im komplett verwahrlosten Taxi quer durch Bayern")
 = 71e8383a4cea32d6fd6877495db2ee353542f46fa44bc231
   00bca48f3366b84e809f0708e81041f427c6d5219a286677

SHA384("Frank jagt im komplett verwahrlosten Taxi quer durch Bayern")
 = ef9cd8873a92190f68a85edccb823649e3018ab4da3aeff5
   4215187c0972f7d77922c72f7c0d90fca01cf3e46af664d2

Der Hash eines Strings der Länge Null ist:

SHA384("")
 = 38b060a751ac96384cd9327eb1b1e36a21fdb71114be0743
   4c0cc7bf63f6e1da274edebfe76f65fbd51ad2f14898b95b

SHA-512

SHA512("Franz jagt im komplett verwahrlosten Taxi quer durch Bayern")
 = af9ed2de700433b803240a552b41b5a472a6ef3fe1431a722b2063c75e9f0745
   1f67a28e37d09cde769424c96aea6f8971389db9e1993d6c565c3c71b855723c

SHA512("Frank jagt im komplett verwahrlosten Taxi quer durch Bayern")
 = 90b30ef9902ae4c4c691d2d78c2f8fa0aa785afbc5545286b310f68e91dd2299
   c84a2484f0419fc5eaa7de598940799e1091c4948926ae1c9488dddae180bb80

Der Hash eines Strings der Länge Null ist:

SHA512("")
 = cf83e1357eefb8bdf1542850d66d8007d620e4050b5715dc83f4a921d36ce9ce
   47d0d13c5d85f2b0ff8318d2877eec2f63b931bd47417a81a538327af927da3e

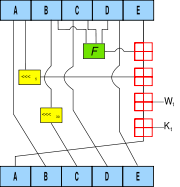
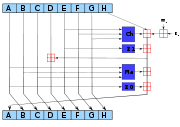
SHA-1 Pseudocode

Es folgt der Pseudocode für den SHA-1.

// Beachte: Alle Variablen sind vorzeichenlose 32-Bit-Werte und
// verhalten sich bei Berechnungen kongruent (≡) modulo 2^32

// Initialisiere die Variablen:
var int h0 := 0x67452301
var int h1 := 0xEFCDAB89
var int h2 := 0x98BADCFE
var int h3 := 0x10325476
var int h4 := 0xC3D2E1F0

// Vorbereitung der Nachricht 'message':
var int message_laenge := bit_length(message)
erweitere message um bit "1"
erweitere message um bits "0" bis Länge von message in bits ≡ 448 (mod 512)
erweitere message um message_laenge als 64-Bit big-endian Integer

// Verarbeite die Nachricht in aufeinander folgenden 512-Bit-Blöcken:
für alle 512-Bit Block von message
   unterteile Block in 16 32-bit big-endian Worte w(i), 0 ≤ i ≤ 15

   // erweitere die 16 32-bit-Worte auf 80 32-bit-Worte:
   für alle i von 16 bis 79
       w(i) := (w(i-3) xor w(i-8) xor w(i-14) xor w(i-16)) leftrotate 1

   // Initialisiere den Hash-Wert für diesen Block:
   var int a := h0
   var int b := h1
   var int c := h2
   var int d := h3
   var int e := h4

   // Hauptschleife:
   für alle i von 0 bis 79
       wenn 0 ≤ i ≤ 19 dann
           f := (b and c) or ((not b) and d)
           k := 0x5A827999
       sonst wenn 20 ≤ i ≤ 39 dann
           f := b xor c xor d
           k := 0x6ED9EBA1
       sonst wenn 40 ≤ i ≤ 59 dann
           f := (b and c) or (b and d) or (c and d)
           k := 0x8F1BBCDC
       sonst wenn 60 ≤ i ≤ 79  dann
           f := b xor c xor d
           k := 0xCA62C1D6
       wenn_ende

       temp := (a leftrotate 5) + f + e + k + w(i)
       e := d
       d := c
       c := b leftrotate 30
       b := a
       a := temp

   // Addiere den Hash-Wert des Blocks zur Summe der vorherigen Hashes:
   h0 := h0 + a
   h1 := h1 + b
   h2 := h2 + c
   h3 := h3 + d
   h4 := h4 + e

digest = hash = h0 append h1 append h2 append h3 append h4 //(Darstellung als big-endian)

Beachte: Anstatt der Original-Formulierung aus dem FIPS PUB 180-1 können alternativ auch folgende Formulierungen verwendet werden:

(0  ≤ i ≤ 19): f := d xor (b and (c xor d))         (Alternative)

(40 ≤ i ≤ 59): f := (b and c) or (d and (b or c))   (Alternative 1)
(40 ≤ i ≤ 59): f := (b and c) or (d and (b xor c))  (Alternative 2)
(40 ≤ i ≤ 59): f := (b and c) + (d and (b xor c))   (Alternative 3)

Siehe auch

• Kryptographie
• Zyklische Redundanzprüfung (ZRP, engl. CRC)
• Prüfsumme
• Hamming-Code
• Elliptische-Kurven-Kryptosystem
• Parität
• MD5

Weblinks

• FIPS PUB 180-2, Secure Hash Standard
• RFC 3174, US Secure Hash Algorithm 1 (SHA1)

zu den Schwächen von SHA

• Pressemitteilung der GI Fachgruppe Krypto: Hashfunktion SHA-1 offenbar gebrochen
• heise online (19.08.2005): Angriffe auf Hash-Algorithmus SHA-1 weiter vereinfacht
• heise online (25.08.2006): Hash-Funktion SHA-1 in Bedrängnis
• Bruce Schneier: SHA-1 Broken (englisch)
• Arjen Lenstra: Further progress in hashing cryptanalysis (englisch, PDF)
• Xiaoyun Wang, Yiqun Lisa Yin, Hongbo Yu: Finding Collisions in the Full SHA-1 (englisch, PDF)
• Cryptographic Hash Project
• SHA-1 Collision Search Graz – das DC-Projekt der TU-Graz