Satz von Casey

äußere Tangentenabschnitte: t₂₃,t₃₄,t₂₄
innere Tangentenabschnitte: t₁₂,t₁₃,t₄₁
Tangenten-Außenseiten: t₁₂,t₂₃,t₃₄,t₄₁
Tangenten-Diagonalen: t₁₃,t₂₄
Casey-Bedingung: t₁₂t₃₄ + t₁₄t₂₃ = t₁₃t₂₄

Der Satz von Casey ist ein nach dem irischen Mathematiker John Casey benannter Satz der Elementargeometrie. Er stellt eine Erweiterung des Satzes von Ptolemäus dar und beschreibt wie sich die Tangentenabschnitte von vier Kreisen in einer bestimmten Konfiguration verhalten.

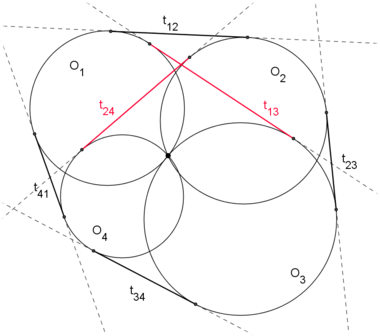
Seien O₁,O₂,O₃,O₄ 4 im Uhrzeigersinn nummerierte Kreise, die alle einen fünften Kreis O berühren. Wenn die Kreise O_i und O_j dann O beide von innen oder beide von außen berühren, so sei t_ij die Länge eines äußeren Tangentenabschnittes, der die Kreise O_i und O_j verbindet. Wenn die beiden Kreise stattdessen O von innen und außen berühren, dann sei t_ij die Länge eines inneren Tangentenabschnittes. Es gilt nun die folgende Beziehung: $\,t_{12} \cdot t_{34}+t_{14} \cdot t_{23}=t_{13}\cdot t_{24}$

Fasst man die Tangtenabschnitte von in der Nummerierung benachbarten Kreise als "Tangenten-Außenseiten" (schwarz) und die nicht benachbarten als "Tangenten-Diagonalen" (rot) auf, so lässt sich der Satz auch so formulieren:

Die Summe der Produkte der gegenüberliegenden Tangenten-Außenseiten entspricht dem Produkt der Tangenten-Diagonalen.

Die Gleichung $t_{12} \cdot t_{34}+t_{14} \cdot t_{23}=t_{13}\cdot t_{24}$ wird als Casey-Bedingung bezeichnet.

Erweiterungen und Anwendungen

Lässt man die Radien der Kreise O₁,O₂,O₃,O₄ gegen Null gehen, so gehen sie im Grenzfall zu Punkten auf dem Kreis O über und die Tangentenabschnitte werden zu den Seiten und Diagonalen eines Sehnenvierecks. Man erhält also den Satz des Ptolemäus als Grenzfall.

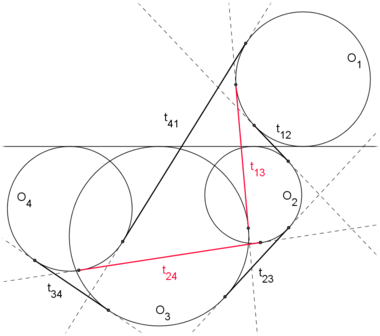
Der Satz von Casey bleibt auch gültig, wenn es sich bei O um einen entarteten Kreis, d.h. einen Punkt (Radius null) oder eine Gerade (Radius unendlich), handelt. Es gelten somit die beiden folgenden Sätze:

Schneiden sich 4 Kreise in einem Punkt, so gilt die Casey-Bedingung: $t_{12} \cdot t_{34}+t_{14} \cdot t_{23}=t_{13}\cdot t_{24}$	Besitzen 4 Kreise eine gemeinsame Tangente, so gilt die Casey-Bedingung: $t_{12} \cdot t_{34}+t_{14} \cdot t_{23}=t_{13}\cdot t_{24}$

Die Umkehrung des Satzes von Casey ist ebenfalls richtig, das heißt es gilt der folgende Satz:

Erfüllen 4 Kreise die Casey-Bedingung, so trifft einer der drei folgenden Fälle zu:

1. alle 4 Kreise haben einen gemeinsamen Berührkreis
2. alle 4 Kreise haben eine gemeinsame Tangente
3. alle 4 Kreise schneiden sich in einem Punkt.

Geschichte

Sangaku-Problem (Gunma-Präfektur 1874)

Innerhalb der westlichen Mathematik wurde der Satz zuerst von John Casey publiziert, allerdings war ein Spezialfall des Satzes, bei dem die 4 berührenden Kreis zusätzlich in ein Quadrat eingeschrieben sind, auch in der japanischen Mathematik der Edo-Periode (Wasan) bekannt. Er ist unter Anderem in Form eines Sangaku-Problems von 1874 aus der Gunma-Präfektur ^[1] erhalten geblieben und war auch schon um 1820 dem Mathematiker Chochu Siraishi bekannt.^[2]

Literatur

• Roger A. Johnson: Advanced Euclidean Geometry. Dover 2007, ISBN 978-0-486-46237-0, S. 121-127 (Erstveröffentlichung 1929 bei der Houghton Mifflin Company (Boston) unter dem Titel Modern Geometry).
• O. Bottema, Reinie Erne: Topics in Elementary Geometry. Springer 2008, ISBN 978-0-387-78130-3, Kapitel The Theorems of Ptolemy and Casey.

Weblinks

• Eric W. Weisstein: Casey's theorem. In: MathWorld. (englisch)
• Shailesh Shirali: On a generalized Ptolemy Theorem

Einzelnachweise

1. ↑ Weisstein, Eric W. "Casey's Theorem." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/CaseysTheorem.html
2. ↑ Christiane Hartmann: Sangaku - Japanische Tempelgeometrie. (Hausarbeit zum Staatsexamen Julius-Maximilians-Universität Würzburg 2008)