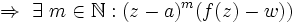Satz von Casorati-Weierstrass
- Satz von Casorati-Weierstrass
-
Der Satz von Weierstraß-Casorati (nach Karl Weierstraß und Felice Casorati) ist ein Satz aus der Funktionentheorie und beschäftigt sich mit dem Verhalten holomorpher Funktionen in Umgebungen wesentlicher Singularitäten. Er hat aber eine schwächere Aussage als die Sätze von Picard.
Der Satz
Sei 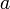 wesentliche Singularität der holomorphen (analytischen) Funktion
wesentliche Singularität der holomorphen (analytischen) Funktion 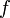 , dann liegt für jede Umgebung
, dann liegt für jede Umgebung 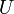 von
von 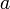 das Bild
das Bild 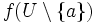 dicht in
dicht in 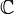 .
.
Anders formuliert: Eine analytische Funktion kommt in der Umgebung einer wesentlichen Singularität jeder komplexen Zahl beliebig nahe.
Beweis
Der Beweis wird indirekt geführt. Es wird also angenommen, dass eine Umgebung U der wesentlichen Singularität a existiert, sodass die Bildmenge 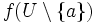 nicht dicht in
nicht dicht in 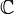 liegt.
liegt.
Dann gilt
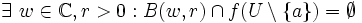 ,
,
wobei B(w,r) den Kreis mit Mittelpunkt w und Radius r bezeichnet. Daraus schließen wir weiter
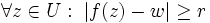
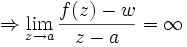 ,
,
also ist a ein Pol von 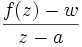
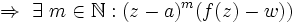 beschränkt.
beschränkt.
Mit der Dreiecksungleichung erhält man die Abschätzung
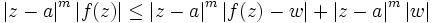 .
.
Da die beiden Summanden auf der rechten Seite beschränkt sind, gilt dies auch für den Ausdruck auf der linken Seite.
Damit ist aber 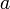 eine Polstelle von
eine Polstelle von 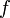 , was wiederum im Widerspruch zur Annahme „
, was wiederum im Widerspruch zur Annahme „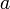 ist wesentliche Singularität“ steht.
ist wesentliche Singularität“ steht.
Siehe auch
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
Satz von Weierstrass-Casorati — Der Satz von Weierstraß Casorati (nach Karl Weierstraß und Felice Casorati) ist ein Satz aus der Funktionentheorie und beschäftigt sich mit dem Verhalten holomorpher Funktionen in Umgebungen wesentlicher Singularitäten. Er hat aber eine… … Deutsch Wikipedia
Satz von Weierstrass — Folgende Sätze werden nach Karl Weierstraß als Satz von Weierstraß bezeichnet: der Satz vom Minimum und Maximum zur Existenz von Extrema der Satz von Bolzano Weierstraß über konvergente Teilfolgen der Satz von Stone Weierstraß über die… … Deutsch Wikipedia
Weierstrass — Karl Weierstraß Karl Theodor Wilhelm Weierstraß (* 31. Oktober 1815 in Ostenfelde bei Ennigerloh/Münsterland; † 19. Februar 1897 in Berlin) war ein deutscher Mathematiker, der sich vor allem um die logisch fundierte Aufarbeitung der Analysis… … Deutsch Wikipedia
Karl Weierstrass — Karl Weierstraß Karl Theodor Wilhelm Weierstraß (* 31. Oktober 1815 in Ostenfelde bei Ennigerloh/Münsterland; † 19. Februar 1897 in Berlin) war ein deutscher Mathematiker, der sich vor allem um die logisch fundierte Aufarbeitung der Analysis… … Deutsch Wikipedia
Karl Theodor Weierstraß — Karl Weierstraß Karl Theodor Wilhelm Weierstraß (* 31. Oktober 1815 in Ostenfelde bei Ennigerloh/Münsterland; † 19. Februar 1897 in Berlin) war ein deutscher Mathematiker, der sich vor allem um die logisch fundierte Aufarbeitung der Analysis… … Deutsch Wikipedia
Karl Theodor Wilhelm Weierstraß — Karl Weierstraß Karl Theodor Wilhelm Weierstraß (* 31. Oktober 1815 in Ostenfelde bei Ennigerloh/Münsterland; † 19. Februar 1897 in Berlin) war ein deutscher Mathematiker, der sich vor allem um die logisch fundierte Aufarbeitung der Analysis… … Deutsch Wikipedia
Weierstraß — Karl Weierstraß Karl Theodor Wilhelm Weierstraß (* 31. Oktober 1815 in Ostenfelde bei Ennigerloh/Münsterland; † 19. Februar 1897 in Berlin) war ein deutscher Mathematiker, der sich vor allem um die logisch fundierte Aufarbeitung der Analysis… … Deutsch Wikipedia
Georg Friedrich Bernhard Riemann — Bernhard Riemann Georg Friedrich Bernhard Riemann (* 17. September 1826 in Breselenz bei Dannenberg (Elbe); † 20. Juli 1866 in Selasca bei Verbania am Lago Maggiore) war ein deutscher Mathem … Deutsch Wikipedia
Karl Weierstraß — ist auf der Ehrentafel ehemaliger Schüler d … Deutsch Wikipedia
Bernhard Riemann — 1863 Georg Friedrich Bernhard Riemann (* 17. September 1826 in Breselenz bei Dannenberg (Elbe); † 20. Juli 1866 in Selasca bei Verbania am Lago Maggiore) war ein deutscher Mathematiker, der … Deutsch Wikipedia
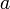 wesentliche Singularität der holomorphen (analytischen) Funktion
wesentliche Singularität der holomorphen (analytischen) Funktion 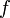 , dann liegt für jede Umgebung
, dann liegt für jede Umgebung 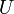 von
von 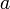 das Bild
das Bild 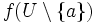 dicht in
dicht in 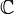 .
.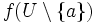 nicht dicht in
nicht dicht in 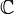 liegt.
liegt.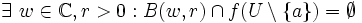 ,
,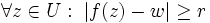
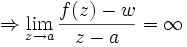 ,
,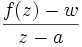
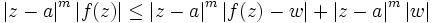 .
.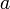 eine Polstelle von
eine Polstelle von 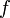 , was wiederum im Widerspruch zur Annahme „
, was wiederum im Widerspruch zur Annahme „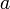 ist wesentliche Singularität“ steht.
ist wesentliche Singularität“ steht.