Satz von Feuerbach

Feuerbachkreis

Der Feuerbachkreis ist ein besonderer Kreis im Dreieck, der nach Karl Wilhelm Feuerbach benannt ist. Auf ihm liegen neun ausgezeichnete Punkte:

• die Mittelpunkte der Seiten;
• die Fußpunkte der Höhen;
• die Mittelpunkte der oberen Höhenabschnitte (das sind die Mittelpunkte der Strecken zwischen jeweils einer Dreiecksecke und dem Höhenschnittpunkt des Dreiecks).

Hier sind D, E und F die Seitenmittelpunkte, G, H und I die Höhenfußpunkte, J, K und L die Mittelpunkte der oberen Höhenabschnitte und S der Höhenschnittpunkt.

Sonderfälle

• Der Feuerbachkreis geht genau dann durch eine Ecke des Dreiecks (nämlich den Scheitel des rechten Winkels), wenn das Dreieck rechtwinklig ist.
• Der Feuerbachkreis berührt genau dann eine Dreiecksseite (nämlich die Basis), wenn das Dreieck gleichschenklig ist.
• Der Feuerbachkreis stimmt genau dann mit dem Inkreis überein, wenn das Dreieck gleichseitig ist.

Eigenschaften

Feuerbachkreis, Inkreis und Ankreise

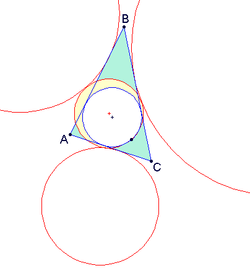
• Der Feuerbachkreis berührt den Inkreis des Dreiecks einschließend und die drei Ankreise des Dreiecks ausschließend, diese Eigenschaft wird auch als der Satz von Feuerbach bezeichnet. Der Punkt, in dem sich Feuerbachkreis und Inkreis berühren, wird Feuerbachpunkt des Dreiecks genannt. (Vorsicht: Manche, meist deutsche, Autoren bezeichnen den Mittelpunkt des Feuerbachkreises als "Feuerbachpunkt".)

• Der Mittelpunkt des Feuerbachkreises liegt genau in der Mitte zwischen Höhenschnittpunkt und Umkreismittelpunkt, also auch auf der Eulerschen Gerade.

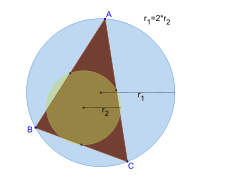
• Der Radius des Feuerbachkreises ist halb so groß wie der Umkreisradius des Dreieckes.

Feuerbachkreis und Umkreis

• Der Feuerbachkreis halbiert die Strecke zwischen dem Höhenschnittpunkt und einem beliebigen Punkt auf dem Umkreis.

• Geht eine gleichseitige (rechtwinklige) Hyperbel durch die Ecken eines Dreiecks, dann liegt ihr Mittelpunkt auf dem Feuerbachkreis.

• Der Mittelpunkt der Kiepert-Hyperbel liegt auf dem Feuerbachkreis.

Koordinaten

Mittelpunkt des Feuerbachkreises (X5)
Trilineare Koordinaten	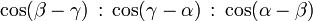$\cos(\beta-\gamma) \,: \, \cos(\gamma-\alpha) \,: \, \cos(\alpha-\beta)$
Baryzentrische Koordinaten	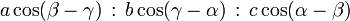$a \cos(\beta-\gamma) \,: \, b \cos(\gamma-\alpha) \,: \, c \cos(\alpha-\beta)$

Geschichtliches

Historisch gesehen ist anzumerken, dass der Feuerbachkreis ein Jahr vor der Veröffentlichung der diesbezüglichen Schrift Feuerbachs, also 1821, von Charles-Julien Brianchon und Jean Victor Poncelet entdeckt wurde. In Deutschland hat sich aber der Name Feuerbachkreis eingebürgert. Grund dafür ist der von Feuerbach stammende, relativ schwierige Beweis, dass dieser Kreis den Inkreis und die Ankreise berührt. In der übrigen Welt sagt man meistens Neunpunktekreis. Es ist auch die historisch gesehen gerechtere Bezeichnung Eulerkreis verbreitet.

Literatur

• Max Koecher, Aloys Krieg: Ebene Geometrie, 3. Aufl., Springer-Verlag, Berlin 2007, ISBN 978-3-540-49327-3
• C. S. Ogilvy: Unterhaltsame Geometrie ISBN 3528283149, ISBN 978-3528283148

Weblinks

• Landesbildungsserver-BW - animierte GeoGebra Arbeitsblätter mit Schiebeschaltern zum Feuerbachkreis mit Beweisen, Folgerungen und Hinweisen.
• Feuerbachkreis.html - eine Visualisierung des Feuerbachkreises mit GeoGebra
• Feuerbach_in_ankreise.html - eine Visualisierung von Feuerbachkreis, Inkreis und Ankreisen des Dreiecks mit GeoGebra
• Feuerbach_umkreis.html - eine Visualisierung von Feuerbachkreis und Umkreis mit GeoGebra
• Feuerbach_U_T_H.html - eine Visualisierung von Feuerbachkreis, Umkreis und einer Strecke von einem verschiebbaren Punkt des Umkreises zum Höhenschnittpunkt; erstellt mit GeoGebra

Siehe auch

Umkreis, Inkreis, Ankreis, Ausgezeichnete Punkte im Dreieck, Eulersche Gerade